Most people think of a machine as being a more or less complicated piece of mechanism which includes gear wheels, levers, screws and so on. But however complex a machine may appear to be, its various parts can always be shown to be applications of a limited number of basic mechanical principles.
Essentially, a machine is any device by means of which a force applied at one point can be used to overcome a force at some other point.
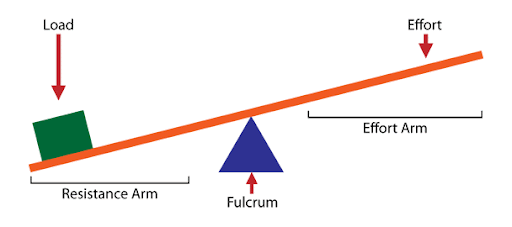
The lever
The simplest form of lever in common use is a steel rod known as a crowbar ( see its image ), but the term lever may be applied to any rigid body which is pivoted about an axis called the fulcrum.
Levers are based on the principle of moments.
A force called the effort is applied at one point on the lever, and this overcomes a force called the load at some other point. Incidentally, the terms of effort and load are not restricted to levers but apply to all types of machines.
If a lever can be used to overcome a load of 50 N by applying an effort of 10 N, the lever is said to have a mechanical advantage of 50/10 or 5.
Some machines are designed to overcome a load much greater than the effort used, for example,
In such cases the mechanical advantage is greater than 1.
In certain other machines the mechanical advantage is less than 1, and in these the effort is greater than the load.
It is not generally realized that a bicycle is a machine with a mechanical advantage of less than 1.
Under ordinary conditions the resistance to the motion of a bicycle along a level road is comparatively small, and therefore a large mechanical advantage is unnecessary. Thus, although a cyclist works at “ mechanical disadvantage”, he nevertheless gains in the speed with which he can travel.
On the other hand, the fact that the mechanical advantage of a bicycle is less than 1 becomes painfully obvious when we begin to ascend a hill. Whereas previously only a small amount of work had to be done against friction and air resistance, we now have to do a vastly increased amount against our own weight and that of the bicycle.
Under these conditions it is usually easier to dismount and walk, unless the mechanical advantage of the bicycle can be increased by using a low gear – will be discussed later –.
Mechanical advantage of a lever
If we neglect friction at the fulcrum and the weight of the lever itself ( both being comparatively small in most cases) the mechanical advantage in any particular case may be obtained by writing down the equation of moments for the load and effort about the fulcrum.
Remembering that
moment = force × perpendicular distance from fulcrum.
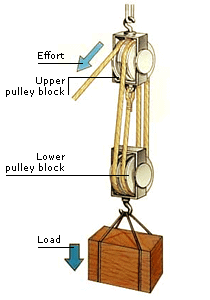
Block and tackle system:

Crowbar:

First class lever:
Wheelbarrow:
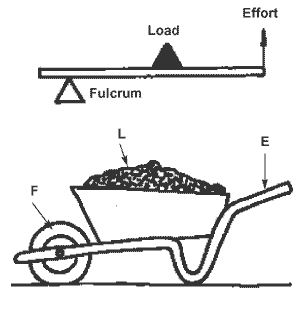
The mechanical advantage in any particular case depends on the position of the fulcrum in relation to the effort and load.
A pulley is a wheel with grooved rim, and there may be several of these mounted in a framework called a block. The effort is applied to a rope which passes over the pulleys.
This is often used for the purpose of raising small loads contained in a bucket or basket to the top of a building during construction or repair work.
The tension is the same throughout the rope, so that, neglecting the weight of the rope itself and any friction in the pulley bearings, we have,
load = effort
and mechanical advantage = load / effort = 1
In this case, although the effort applied is equal to the load raised, we obtain the greater convenience and ease of being able to stand on the ground and pull downwards, instead of having to haul the load upwards from the top of the building.
Here the tension in the string or rope is equal to the effort applied, so that the total upward pull on the pulley is twice the effort E.
Suppose a load of 4 N is supported by the pulley and that the weight of the pulley block and string is negligible. Then, since the load is supported by the tension in two sections of string, the effort applied need only be 2 N. Thus,
mechanical advantage = load / effort = 4 / 2 = 2.
Labels: Classical mechanics