“Pressure” is a word we use from day to day without worrying too much as to its exact meaning.
Before setting out on a car journey we make sure that the air pressure in the tyres has been correctly adjusted, not only to keep within the law, but for our own safety and that of others.
Steam boilers have gauges fitted to measure the steam pressure.
At home, in the kitchen, there may be a “pressure cooker” and so on.
In physics,however, little progress is made until we are able to measure the things we talk about. So we must always define or state the exact meaning of the words we use.
Pressure is defined as the force acting normally per unit area. ( Here, the word "normally" means perpendicularly).
The SI unit of pressure is 1 newton per metre² ( N/m²).
pressure = force/area ( F / A).
You can see that one does not have to use great force when using a very sharp knife. Owing to the very small area of the cutting edge, even a moderate force will create a very high pressure. The same principle applies to the piercing action of a needle or other sharp point.
Here on earth we are living at the bottom of a sea of air. Air has weight. Owing to its weight the atmosphere exerts a pressure of approximately 100000 N / m².
Now, the atmospheric pressure acts not only on the earth’s surface but all over the surface of objects on the earth, including ourselves.
An average-sized man having a surface area of 2 m² will therefore have a total thrust (force) acting over his body of something in the region of 200 kN! He is not of course, conscious of this enormous load, since his blood exerts a pressure of slightly greater than the atmospheric pressure, and so a balance is more than effected.
At high altitudes, where the pressure of the air is less, nose-bleeding may occur owing to the greater pressure of the blood.
Until the seventeenth century it was not realized that the atmosphere did exert a pressure, and men explained its effects by saying that “nature abhorred a vacuum”.
Thus the common experience that when air is sucked out of a bottle it immediately tries to rush back in again was explained by the theory that nature could not tolerate a vacuum.
Nowadays, we say that the excess atmospheric pressure outside the bottle causes a flow of air into the bottle until the pressure inside and outside are equalized.
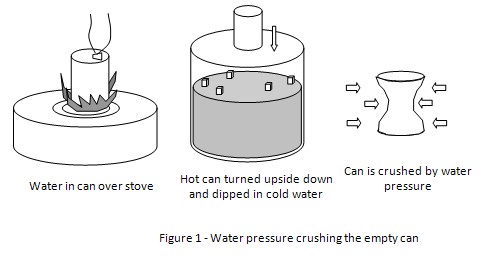
The large forces which can be produced by atmospheric pressure may be demonstrated by means of a metal can fitted with an airtight stopper.
Crushing can experiment: 
The stopper having been removed, a small quantity of water is boiled in the can for a few minutes until the steam has driven out the air.
The cork is then tightly replaced and simultaneously the flame beneath the can is turned out.
The Magdeburg hemispheres (poor horses!)
In 1654 a German scientist named Otto von Guericke made two hollow bronze hemispheres, one of which had a stop-cock.
After the rims of these had been placed together with a greased leather ring in between to form an airtight joint the air was pumped out and the stop-cock closed.
Before this was done the hemispheres could be pulled apart quite easily, since the pressure outside was balanced by an equal pressure inside.
On removal of the air from inside, only the external atmospheric pressure acted and pressed the hemispheres tightly together.
This experiment was first performed before the Imperial Court assembled at Ratisbon, on which occasion two teams of eight horses each were harnessed to the hemispheres and driven in opposite directions. They proved unable to separate the hemispheres until air had been readmitted through the stop-cock.
The invention of the air pump by Otto von Guericke led to big advances in the study of air pressure. The image shows the principle of a modern type of pump.
Each time the piston is at the bottom of the cylinder some air from the vessel to be evacuated expands into the space above the piston.
On each upstroke the air above the piston is carried out through the valve A. The oil on top of the piston acts not only as a lubricant and air seal but also fills the dead space between piston and valve at the top of the stroke and ensures removal of all air trapped there.
Vacuum pump diagram: 
Liquids exert pressure in the same way air does.
The pressure in a liquid increases with depth.
This may be shown by means of a tall vessel full of water with side tube fitted at different heights ( see the image below).
The speed with which water spurts out is greatest for the lower jet, showing that pressure increases with depth.
The pressure at any point in a liquid acts in all directions.
This may be demonstrated by the apparatus shown in the image below.
Several thistle funnels bent at different angles have thin rubber securely tied over their mouths. These are connected one at a time by rubber tubing to a U-tube containing water.
If pressure is exerted on the rubber by hand the air inside is compressed and pushes up the water in the U-tube.
So we may regard the whole device as an arrangement for indicating ( though not measuring) pressure.
When the funnels are lowered into water the U-tube indicates a pressure, whichever funnel is in use, thereby showing that pressure in the water acts in all directions.
Pressure increases with depth: 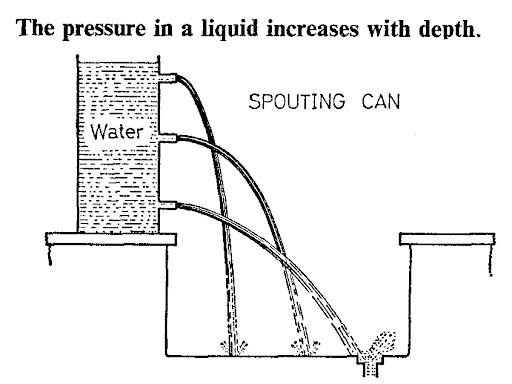
Pressure acts in all directions: 
Suppose we consider a horizontal area A, in m², at a depth of h, in m, below the surface of a liquid of density ρ, in kg/m³.
Standing on this area is vertical column of liquid of volume hA, in m³, the mass of which ( volume × density) is given by hAρ, in kg.
Now we know that the weight or thrust, in newtons, of a body on its support is given by mg, (m in kg, g = 9.8 m/s²). Hence,
Thrust (in N) on area = hAρg
Therefore,
pressure (in N/m²) = thrust/ area = hAρg/A=hρg.
It is important to notice that the area A does not appear in the final expression for the pressure. The pressure at any point in a liquid at rest depends only on the depth and density.
Pressure of a liquid column: 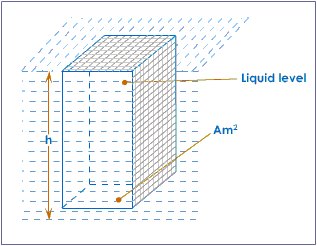
Labels: Fluid mechanics