
In this article:
Direction of a tension on a string
The block and tackle pulley system
Velocity ratio ( or speed ratio) (V.R.)
Work done by a machine. Efficiency
Relation between mechanical advantage, speed ratio, and efficiency
In all pulley diagrams some consideration must be given to the direction in which force arrows are drawn on the string.
Take the case of a 2 kg mass supported by a string held in the hand.
The tension in the string is:
F = mass × acceleration due to gravity ( Newton’s second law of motion )
F = m × g = 2 × 9.8 = 19.6 N.
This tension acts equally in both directions. The arrow pointing upwards represents the force which the string exerts on the load, while the arrow pointing downwards shows the force exerted by the string on the hand. This is another example of Newton’s third law of motion.
In general, we do not put in both arrows, but only the one which gives the direction of the force in which we are interested. Thus in the image shown below both arrows are drawn upwards as we wish to indicate the force exerted by the string on the load. We are not here concerned with the downward pull of the string on the support.

This is by far the most important pulley system of all, being commonly used for lifts and cranes.
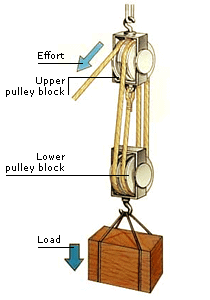
Two blocks are employed containing from two to eight pulleys in each, according to the mechanical advantage required. Now, if an effort E is applied to the free end of the string, then the total upward force on the load will be 2 E.
If we neglect friction and the weight of the moving parts of the system, then,
mechanical advantage = 2 E / E = 2
In practice, however, the practical mechanical advantage in a case such as this is always less than 2, since extra effort must be applied to overcome friction and the weight of the moving pulley block and string.
In the pulley system we have already considered where the mechanical advantage is greater than 1 ( see previous article), It might appear at first sight that we are getting more out of the machine than we are putting into it. But while in such cases the effort moves through a much greater distance than that of the load.

Consequently, the work obtained from the machine is equal to the work put into it, less any work wasted in the machine, but this is discussed more fully in the next section of this article.
Velocity ratio calculation
The ratio of the distance moved by the effort to the distance moved by the load in the same time is called the velocity ratio of the machine, i.e.,
V.R. = distance moved by the effort / distance moved by the load in the same time.
useful work done by a machine If the pulley system were a “ perfect machine”, i.e., composed of weightless and frictionless strings and pulleys, then a load of 4 N would be raised through a distance of 1 m by an effort of 1 N exerted over a distance 4 m.
The work done by a machine on the load is then
Work = force × distance = 1× 4 = 4 joules.
These are equal, as we should expect for a perfect machine. In practice, however, some work is always wasted in overcoming friction and raising moving parts, and therefore the useful work done by a machine is always less than the work done by the effort.
Efficiency of the machine:
The ratio of the useful work done by the machine to the total work put into the machine is called the efficiency of the machine.
Usually, this ratio is expressed as a percentage, so we may write efficiency = work output / work input × 100%
Since,
work = force × distance
it follows that
efficiency = load × distance load moves / effort ×distance effort moves
= M.A. × 1 / velocity ratio
= M.A. / V.R. × 100%
Note that This equation will be found very useful for working out problems, but it is not a fundamental definition of efficiency and should not be used as such.
Labels: Classical mechanics