In the case of separate excitation, the field circuit is electrically independent of the armature circuit (Fig. 1.22) . Therefore the field (or excitation) current is independent of the terminal voltage of the generator and, in consequence, of loading. This makes it possible to regulate the magnetic flux and, hence, the generator voltage over a broad range. To this end the field circuit is extended to include a field rheostat, rf . The field rheostat must be designed and connected so as to prevent any sudden interruption in the excitation current, such as when the supply source, Ef , is disconnected. The point is that the field winding has an appreciable inductance, so an interruption of its circuit may be accompanied by a large emf of self-induction detrimental to the insulation of the field winding and by heavy sparking between the separating contacts.
The power taken by the field excitation circuit accounts for as little as 1-3% of the rated power, so the generator voltage can he controlled in a very economical way.
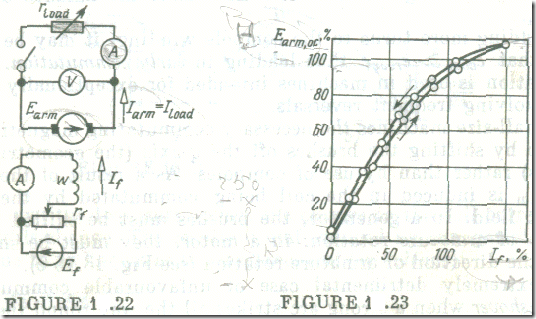
A change in the excitation current brings about a change in tho login magnetic field and in the armature emf proportional to it, Earm = cEΦn .The dependence of the emf on the excitation current with the" armature circuit open (Iarm = 0) and with the speed (rpm) held constant , n = const, is called the open-circuit characteristic of a machine, Earm,oc = F (If). When drawn to a different scale, it can serve as the magnetization curve.
When the field circuit is open (If = 0), the frame of the machine retains some residual magnetic induction. When the armature rotates in the field due to the residual magnetic induction in the absence of armature current, a small open-circuit emf, Earm,oc , is induced in the armature winding.
The open-circuit characteristic of a machine is plotted by applying a voltage to the field winding and gradually increasing the excitation current to its maximum permissible value while noting the values of emf. This produces the up-sloping portion of the characteristic (see Fig. 1.23)."Then the excitation current is gradually reduced, and the corresponding values of emf are again noted and plotted to give the down-sloping part of the characteristic. It usually lies somewhat above the up-sloping part due to hysteresis. If, now, the excitation current is turned off, the residual magnetic induction and the corresponding emf will he greater than they were initially. However this residual magnetic induction is not stable and a short time after the excitation current is turned off, the flux and the emf it induces as the armature rotates go down to their initial values.
Thus, the open-circuit characteristic is the shape of a loop which is a natural consequence of hysteresis (see Fig. 6.5 b) in the magnetic circuit of the machine, mainly its substantial frame. At the top the open-circuit curve has a smaller slope due to saturation in the magnetic circuit of the machine. In most cases d.c. generators operate within the saturation region of the open-circuit characteristic. Owing to saturation the generator voltage is less subject to variations with changes in loading, because the effect of armature reaction on the emf of the machine is reduced.
Another important characteristic of a d.c. generator is the dependence of the terminal voltage V on the armature current Iarm , with the field current If , and the speed n held constant. This dependence is called the load or external characteristic (Fig. 1.24). Experimentally it is plotted as follows. The generator is first loaded to the rated current Irtd, with the terminal voltage held at its rated Value. The terminal voltage is set at its rated value by adjusting the field current If . Then the armature current is gradually decreased to zero. In the circumstances, the field current of a separately excited d.c. generator will remain unchanged.
The terminal voltage of a separately excited d.c. generator is somewhat smaller than its emf due to the voltage drop across the resistance, rarm, of the armature winding and the brush contact resistance
V = Earm — rarmIarm
If the armature emf, Earm, remained constant, the V (Iarm) plot would yield a straight line (shown dashed in Fig. 1.24). However, as load is increased, the useful magnetic flux of the machine decreases mainly due to armature reaction, and so does the proportional armature emf, .Earm . As a result, the external characteristic bends towards the axis of abscissae. On the basis of the external characteristic, it is convenient to find the rated voltage regulation of the machine. It is defined as
that is, as the final change in voltage when the specified load is reduced gradually to zero, expressed as a percent of rated load voltage, the speed and the excitation current being held constant .
For generators without a compensating winding, the voltage regulation ∆Vrtd is about 5-15%.
If we increase the armature current over and above its rated value, the generated voltage will keep falling, but the machine will be overloaded. Its armature winding, brushes and commutator will be heavily heated and a severe sparking will occur under the brushes.
For the normal operation of loads it is essential to maintain the voltage of each of them at a constant value despite variations in the overall loading. This is effected by controlling the field current. The dependence of the field current If on the armature current Iarm with the terminal voltage V and the speed n being held constant, is called the control characteristic of a separately excited d.c. generator. This characteristic shows how the field current should be varied in order to keep the terminal voltage constant despite variations in load. At first this curve is nearly straight (Fig. 1.25), but finally bends upwards due to the saturation of the magnetic circuit of the machine.
Labels: Electricity and Magnetism