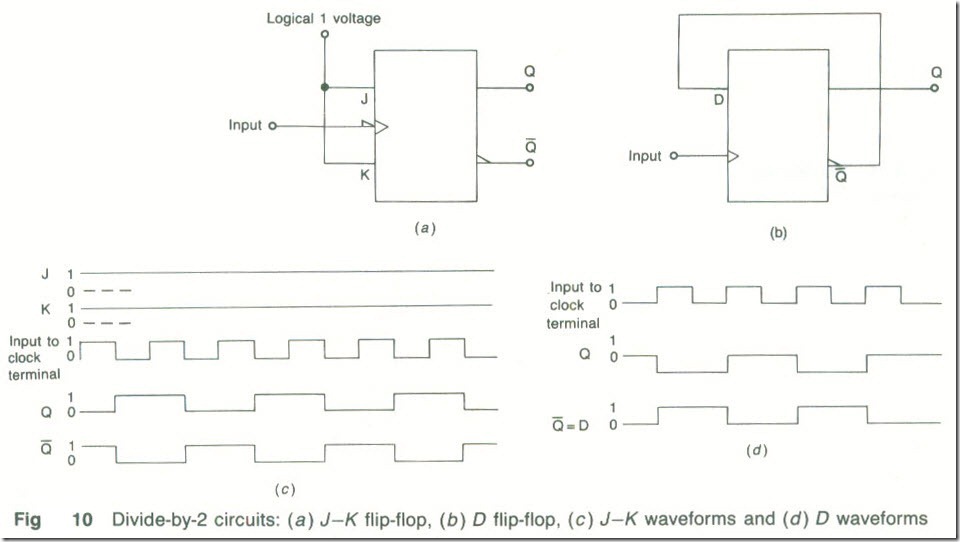
Two ways of obtaining a divide-by-two counter are shown by Figs .10(a) and (b). The J-K flip-flop circuit in (a) has both its J and K inputs held permanently at logical 1. The circuit toggles at the end of each clock pulse and generates an output pulse waveform at one-half the clock frequency. The circuit waveforms are given in Fig. 10(c). The D flip-flop can be converted to operate as a divide-by-2 counter by connecting its D and Ǭ terminals together as shown in Fig .10(b). The circuit's input and output waveforms are given in Fig .10(d). At the first leading edge of the clock, when Q = 1 and Ǭ = 0 so that D = 0, the circuit switches to have Q = 0. Now Ǭ = D = 1 and on the leading edge of the second clock pulse the circuit switches again so that Q = 1, Ǭ = 0 and so on.
Divide-by-4 Counter
If two J-K, or two D, nip-flops are cascaded. Fig .11, a divide-by-4 counter will be produced. Consider the J-K circuit and suppose that initially both stages are reset (QA = QB = 0). The trailing edge of the first clock pulse (input pulse) will toggle flip-flop A and QA will change from 0 to 1. The other flip-flop will be unaffected. The second pulse will again toggle flip-flop A and make QA change from 1 to 0. This is the trailing edge of a pulse so that flip-flop B also toggles to give QB = 1. Thus, after two input pulses the state of the counter is QA = 0, QB = 1 . A third input pulse will cause FFA to toggle again but the change from 0 to 1 in QA will have no effect on FFB. Now both flip-flops are set and QA = QB = 1.
A fourth input pulse toggles FFA and QA changes from 1 to 0; this change causes FFB to toggle also and so QA = QB = 0. The count sequence is now complete and any more input pulses will make the circuit count through the same sequence once again. The circuit waveforms are shown by Fig .12.
Divide-by-8 Counter
A divide-by-8 counter requires three flip-flops connected in cascade and Figs. 13(a) and (b) show the J-K and D flip-flop versions, respectively. This time the operation of the D flip-flop circuit will be described. Suppose that all three flip-flops are initially reset so that QA = QB = Qc = 0 and DA = DB = Dc = 1.
(a) At the end of input pulse 1 FFA changes state to have QA = 1, DA = 0 . FFB and FFC are unaffected.
(b) At the end of input pulse 2 FFA changes state to QA = 0, DA = 1, The change in QA from 1 to 0 causes FFB to change state. Now: QA = 0, QB = 1; DA = 1, DB = 0. FFC is unaffected.
(c) At the end of input pulse 3 FFA changes state to QA = 1 , DA = 0. The change in QA from 0 to 1 does not affect either FFB or FFC. Now QA = QB = 1. DA = DB = 0.
(d) At the end of input pulse 4 FF/4 changes state to QA = 0 , DA = 1 . This is the trailing edge of a pulse so that FFB switches to have QB = 0 , DB = 1. The change in QB from 1 to 0 causes FFC to switch from RESET to SET and have Qc = 1 , Dc = 0. Now the counter state is QA = QB = 0 , Qc = 1 .
The counter carries on with this sequence until the seventh input pulse is applied when QA = QB = Qc = 1 . An eighth input pulse will then reset all stages to give QA = QB = Qc = 0. Thus the circuit has eight different states and a maximum count of 111 or decimal 7.
Labels: electronics