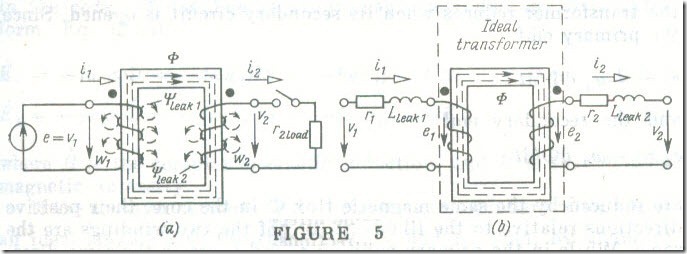
In sketch form, the arrangement of a single-phase transformer is shown in Fig. 5 a. On the secondary side, where the winding has W2 turns, the transformer acts as a supply source for a load
whose resistance is r2,load . On the primary side, where the winding has W1 turns, it acts as a load with respect to its own power supply.
To begin with, suppose that the secondary circuit of the transformer is open and that the supply voltage V1 = e causes a current i1 to flow in its primary winding. The mmf i1w1 induces in the core a magnetic flux whose positive direction is determined by the corkscrew rule (see Fig. 1 a). This flux induces an emf of self-induction, eL1, in the primary and an emf of mutual induction, eM2 in the secondary. (Neither of the emfs is shown in the diagram.) When the secondary circuit is completed. the emf of mutual induction eM2 gives rise to a current, i2 , in the load resistance r2,load ·
For the polarity of the primary and secondary windings indicated in Fig. 5 and the assumed positive directions for the currents it and i2 the magnetic flux induced in the core by the mmf i2W2 opposes the magnetic flux due to the mmf i1W1 In consequence, the primary and secondary windings are connected' in opposition. which fact is stated by assigning the same lapels to the winding terminals as were used in this Figure .
Therefore the total mmf of the primary and secondary windings is equal to i1W1 – i2W2 . This mmf induces a common magnetic flux Φ in the core. Also, in analysing the operation of the transformer, we should include the leakage flux linkage of the primary, ψleak,l , and of the secondary, ψleak,2 , each proportional to the respective current, i1 or i2 .
Figure 5 b shows an equivalent circuit of the transformer; it is made up of the resistances r1 and r2 of the primary and secondary windings, and of the respective leakage inductances, Lleak,l = = ψleak,l /i1 and Lleak,2 = ψleak,2 (similarly to Fig. 4).
It is useful to introduce the concept of an ideal transformer, that is, one in which the primary and secondary windings have neither resistance nor leakage flux linkage. In Fig. 5 b it is enclosed in the dashed box. The positive directions for e1 and it in its primary are the same as they are in an iron-cored coil (see Fig. 4) to which the transformer reduces when its secondary circuit is opened. Since the primary emf
e1 = -W1 dΦ/dt
and the secondary emf
e2 = -W2 dΦ/dt
are induced by the same magnetic flux Φ in the core, their positive directions relative to the like terminals of the two windings are the same. While in the primary winding e1 and il are in the same direction, in the secondary e2 and i2 are assigned opposite directions. This corresponds to the physical interpretation of the role played by the emf: in the former case it opposes any change in the current; in the latter case, it gives rise to a current.
To begin with, we will consider an ideal single-phase transformer in which the core is fabricated from a ferromagnetic material having a linear B/H relation, B = μrμ0H (see Fig. 6 c).
As has been noted in Sec. 6.3, the magnetic field in a core is not the same over its cross-sectional area S. For simplicity, we will ignore this fact and assume that both the magnetic induction and the magnetic intensity in the transformer core are everywhere the same as they are at the central magnetic line. If so, the electric circuit of the transformer is linear, and it can be analysed using the complex-number method.
in Fig. 6 an ideal single-phase transformer is shown connected between a source of emf Ė and a load of complex impedance z2 ∠ φ2 ·
Let us write the values of Ė l and Ė 2 induced in the primary and secondary windings of the ideal transformer by the magnetic flux Φ̇ .
in the core. By the law of electromagnetic induction in complex form, Eq. (2.33)
Ė l = -jɷw1Φ̇ = - jɷw1ḂS = -jɷwlμrμ0ḢS (8.1a)
Ė 2 = -jɷw2Φ̇ = - jɷw2ḂS = -jɷw2μrμ0ḢS (8.1b)
where Ḃ is the complex magnetic induction, and Ḣ is the complex magnetic intensity.
If the complex currents in the primary and secondary windings of an ideal single-phase transformer are İ1 and İ2 , then, by virtue of Eq. (6.2), the average magnetic intensity, that is, one at the centre line of the core, is
Ḣ = İ1w1/Ɩav - İ2w2/Ɩav (8.2)
By definition, the source emf is Ė = V̇1 the primary emf is
Ė1 = - V̇1 and the secondary emf is Ė2 = - V̇2 (see Fig. 6). Therefore, subject to Eqs. (8.1) and (8.2),
V̇1 = -jɷw1Φ̇ = jɷwlμrμ0S (İ1w1/Ɩav - İ2w2/Ɩav) (8.3a)
V̇2 = Z2İ2= jɷw2Φ̇ (8.3b)
Notably, at no-load, or in the open-circuit condition, (which implies that the secondary circuit is open and İ2 = 0)
V̇1 = jɷwlμrμ0S (İ1,ocwl/ Ɩav) (8.3c)
where İ1,oc is the open-circuit (or no-load) current also called the magnetizing current.
Since the source emf , Ė1 = V̇1 is a constant quantity, then, by virtue of Eqs. (8.3a) and (8.3c)
İ1w1/Ɩav - İ2w2/Ɩav = İ1,ocw1/Ɩav = const (8.4)
On dividing Eq. (8.3b) by (8.3a) termwise, we get
V2/V1 = w2/w1=n21 (8.5)
which is the turns (or transformation) ratio of an ideal single-phase transformer. on substituting for Φ̇ from (8.3b) into (8.3a), we get
V̇1 = Z2 (w1/w2) İ2 (8.6)
Now we multiply and divide the right-hand side of Eq. (8.6)
by w1/w2
V̇1 = Z2 (w1/w2)2 (w2/w1) İ2 = Z'2 İ'2 (8.7)
where
Z'2 = Z2 (w1/w2)2 = Z2/n221 (8.8)
is the complex impedance of the secondary circuit referred (or transferred) to the primary side or, simply, the referred (transferred) impedance, and
İ'2 = (w2/w1) İ2 = n21İ2 (8.9)
is the complex current in the secondary circuit, referred (or transferred) to the primary side or, simply, the referred (transfer ret!) current.
By invoking the concepts of transferred current and impedance we may re-cast Eqs. (8.4) and (8.3) as
I1 - İ'2 = İ1,oc (8.10a)
V̇'2 = (w1/w2) V̇2 = V̇2/n21 = Z'2 İ'2 (8.10c)
where w22μrμ0S/Ɩav = L1 is the inductance of the primary winding in an ideal single-phase transformer, and V̇'2 is the complex secondary voltage of an ideal single-phase transformer, referred (or transferred) to the primary side or, Simply, the referred (transferred) voltage.
Equations (8.10) correspond to the equivalent circuit shown in Fig. 7 in which the ideal transformer model is enclosed in a dashed box.
A further assumption made for an ideal transformer is that at μr = ∞ , the inductive reactance
L1 is infinitely large and the magnetizing current is İ1,oc = 0 .
With the secondary circuit opened, an ideal single-phase transformer reduces to an ideal iron-cored coil. As a consequence, an ideal single-phase transformer at no-load has the same equivalent circuit as an ideal iron-cored coil (see Fig. 4) on the condition that the coil and the primary winding of the transformer have the same number of turns and the same cores.
Labels: Electricity and Magnetism