At this stage we will consider an ideal single-phase transformer in which the core is fabricated from a ferromagnetic material whose hysteresis has to be included in consideration (see Fig.6 b).
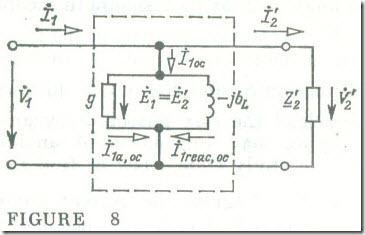
With the secondary circuit open-circuited, this ideal single-phase transformer has the same equivalent circuit as the ideal coil enclosed in the dashed box in Fig. 7 h. On replacing the hysteresis loop of the core with an equivalent ellipse (see Fig. 6), we are in a position to determine the conductance g and the inductive susceptance bL of the ideal coil (see Sec. 7.4). When the secondary circuit is completed through a load (the transformer is in the on-load condition), its equivalent circuit becomes like that shown in Fig. 8.8. Here the ideal single-phase transformer proper is enclosed in a dashed box, and the referred (transferred) secondary circuit is the same as has been considered earlier (see Fig. 7).
The equivalent-circuit parameters g and bL of an ideal single-phase transformer with a core whose hysteresis has to be included in consideration are frequency-dependent. This is because the area of the dynamic hysteresis loop of the core depends on the frequency of the magnetizing current (see Sec. 7.5).
Figure 9 shows the phasor diagram of a loaded ideal single-phase transformer. The magnetic flux phasor Φ̇ is assigned an initial phase of zero. The magnetizing current phasor İ1,oc leads the magnetic flux phasor Φ̇ by the loss angle 6, much asthe current phasor İ does on the phasor diagram for an iron-cored coil (see Fig. 8). The phasors .
representing the emfs Ė1 and Ė2. induced in the primary and secondary windings of an ideal transformer lag behind the magnetic flux phasor by an angle π/2, as they should in accord with Eq. (8.1).
The phasors V̇l and V̇2 respectively representing the voltages between the terminals of the primary and secondary windings are the same in length as the emf phasors Ė1 and Ė2, but, as follows from Eq. (8.3) , the voltage phasors lead the flux phasor Φ̇ by an angle π/2 .
Given the complex load impedance of an ideal transformer, Z2 = z2 ∠ φ2 , we can apply Ohm's law to find the secondary current İ2 = V̇2/Z2 (in the diagram the current phasor İ2 is plotted for φ2 > 0 , that is for an inductive load impedance) and the primary current
İ2 = İ'2 + İ1,oc = (w2/w1) I2 + İ1,oc
Now we will set up an equivalent circuit for a real single-phase transformer (see Fig. 5 b) which has an ideal single-phase transformer as an integral part .
The equivalent circuit of a real single-phase transformer is shown in Fig. 10 where r1 is the resistance of the primary winding, leak,1 = ɷLleak,1 is its inductive leakage reactance, r'2 = r2X (w1/w2)2 is the referred resistance of the secondary winding, and leak,2 = ɷL'leak,2 = ɷLleak,2 X (w1/w2)2 is the referred inductive leakage reactance of the secondary winding The part corresponding to an ideal single phase transformer is enclosed in the dashed box.
Referring to the above equivalent circuit, we can write the following Kirchhoff voltage law equations:
V̇1= - Ė1+ r1İ1 +jleak,1İ1 = - Ė1 +Z1İ1. (8.11a)
V̇2= - Ė2+ r2İ2 +jleak,2İ2 = - Ė2 +Z2İ2. (8.1ib)
where Z1= r1 + jleak,1 and Z2 = r2 + jleak,2İ2 are the complex impedances of the primary and-secondary windings, including their resistances and leakage reactances .
Figure 11 shows a phasor diagram for a real single-phase transformer. It is similar to that for an ideal single-phase transformer (see Fig. 9) .
It follows from the equations of and the phasor diagram for a real single-phase transformer that the relation between the rms voltages across the primary and secondary windings is not the same as that between the rms em1s induced in the same windings by the core magnetic flux Φ̇ .
The rms voltages ZlI1 and Z2I2 are called the total internal voltage drops across the respective windings. It should he remembered that a referred (or transferred) phasor diagram iscorrect only as far as the qualitative relations between the quantities are concerned. In most practical cases the internal voltage drop tri- angles are small, that is, V1 ≈ E1 and V2 ≈ E2 , SO it may be deemed that
V2/ V1 ≈ E2/E1 = w2/w1 = n21 (8.12)
Note that the magnetizing current in a real transformer depends on its load, i.e. on the current İ2 . This may be explained by the fact that the current in and the total internal voltage drop, zlI1 , across the primary winding vary with the load. In most cases, however, the voltage drop, zlI1, is much lower than the supply voltage, V1 therefore the magnetizing current may be considered equal to the open-circuit current of the transformer at İ2 = 0 .
A transformer for which the apparent power rating is Srtd = = S1.rtd = V1.rtd I1.rtd may be in any one of several conditions, namely:
(1) The rated condition when V1 = V1.rtd and I1 = I1.rtd .
(2) The operating condition when the primary voltage is very close or equal to the rated voltage, V1 ≈ V1.rtd , and the primary current I1 depends on the load sustained by the transformer.
(3) The open-circuit condition when the secondary of the transformer is open (I2 = 0) or connected across a load of a very high impedance (such as a voltmeter).
(4) The short-circuit condition in which its secondary is short-circuited (V2 = 0) or connected across a load of a very low impedance (such as an ammeter).
The open-circuit and short-circuit conditions may be produced deliberately for testing purposes, or occur spontaneously as a result of a fault.
Labels: Electricity and Magnetism