Transformer Losses

Transformer Losses

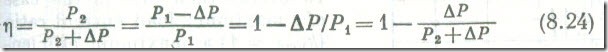
The ratio of the active power P₂ at the output of a transformer to the active power P₁ at its input (see Fig. 4) is called its efficiency

ƞ = P₂/ P₁

or

ƞ% = (P₂/P₁) X 100 (8.23)

When a transformer is operating at its rated primary voltage, V₁ = V₁,_rtd , its rated primary current, I₁ = I₁,_rtd , and a load power factor ( cos φ₂) of over 0.8. the efficiency is very high, being in excess of 99 % for power transformers. For this reason it is never found by directly measuring P₁ and P₂ . The point is that one would have then to measure P₁ and P₂ to an extremely high level of accuracy not at­tainable at the existing state of the art. Fortunately, the efficiency of a transformer can be found indirectly from the transformer losses which can be measured directly. Since the transformer losses are

ΔP = P₁ – P₂

it follows then that the efficiency is

The transformer losses are the sum of the core losses, P_c , and the winding losses, P_w . Given V₁ = V₁,_rtd and I₁ = I₁,_rtd , the core loss­es are equal to the active power of the transformer in the open­ circuit test (see Sec. 8.6), and the winding losses (traditionally cal­led the copper losses) are equal to the active power of the transformer in the short-circuit test (see. Sec. 8.7).

Consider how the efficiency of a transformer varies in operation at the rated primary voltage V₁ = V₁,_rtd into a load whose impedance Z₂ is varying and whose power factor cos φ₂ remains constant. A change in Z₂ brings about a change-In the load power, in the winding cur­rents and. as a consequence, in the winding losses and the transform­er efficiency. The winding losses are also referred to as the transient losses of a transformer. and the core losses are called its steady-state losses .

The winding losses (see Fig.17 a) are given by

r_sc (I'₂)² = k²_loadr_sc (I'_2,rtd)2 = k²_loadP_sc,rtd

where k_10ad is the load current ratio, Eq. (8.22), and P_sc,rtd is the winding losses at rated currents.

As the secondary current is varied from zero to its rated value, it may be assumed that

V₂ ≈ const ≈ V₂,rtd = V₁,_rtd n₂₁

The output active power of a transformer is given by

P₂ = V₂I₂ cos φ₂ = k_10ad V₂I_2,rtd cos φ₂ ≈ k_loadS_rtd cos φ₂

and the efficiency, in accord with Eq. (8.24), is

As is seen, the efficiency of a transformer depends on the load power factor cos φ₂ and the load current ratio k_load . If we hold the load pow­er factor constant and equate to zero the derivative of ƞ with respect to k_load , we will find that the efficiency of a transform­er is a maximum at

k_load = √P_c/P_sc,rtd

It follows then that in the case of a maximum load current ratio (k_load = 1) a maximum efficien­cy can be obtained when the core losses are equal to the wind­ing (or copper) losses.

Actually, the load current ratio of a real transformer is never unity. For this reason, transformers are designed so that their efficiency (Fig. 19) would be a maximum at some average load. For example, for P_c/P_sc,rtd = 0.25-0.5 the efficiency will be a maximum at

K_load = √P_c/P_sc.rtd = 0.5-0.7

Labels: Electricity and Magnetism