Similarly to Eq. (15.9) defining the electric power developed by a three-phase synchronous generator, that taken by a three-phase synchronous motor is given by
P = 3VI cos φ = 3E0I cos φ0 = 3E0I cos (φ - θ) (15.17)
where θ > 0.
Rearranging Eq. (15.17) in the same manner as Eq. (15.9) and noting that θ > 0, we derive an expression for the electromagnetic torque developed by a synchronous motor, similar to that defining the electromagnetic torque of a synchronous generator, Eq. (15.11):
Tem = (3p/2πf) E0V sin θ/ (15.18)
Since the mechanical power developed by a synchronous motor is Pm = P = Temɷrot
then, subject to Eq, (15.18), we get
Pm = P = 3VI cos φ = 3E0V sin θ/ (15.19)
In a large power system the system voltage V and the system frequency f are constant.
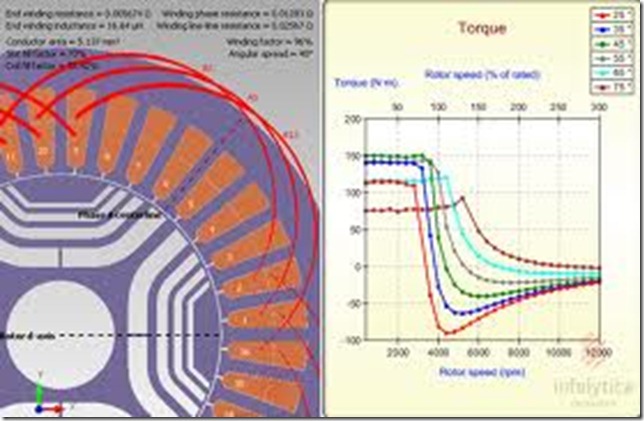
In view of this observation we may conclude that, at a constant field (excitation) current, the electromagnetic torque Tem and the power P developed by a synchronous motor operating as part of a large power system depend solely on the load angle θ . The relations Tem = f (θ) and P = f (θ) are called the torque-angle and power-angle characteristics of a synchronous motor and have the shape similar to that of the load-angle characteristics of a synchronous generator (see Fig 10) . These characteristics give insight into what happens in a synchronous motor as its load is varied. As the load (retarding) torque at the shaft of a synchronous motor increases
Tret.2 > Tret,l = Tem,1
the rotor of the motor slows down, and the load angle θ and the electromagnetic torque Tem begin to increase. The retarding and electromagnetic torques strike a balance, Tret.2 = Tern.2, some time later, at a new value of the load angle, θ2 > θ1 .If we wish to retain the necessary margin of stability, π/2 – θ , at an increased retarding (load) torque, we should increase the field (excitation) current.
Labels: Electricity and Magnetism