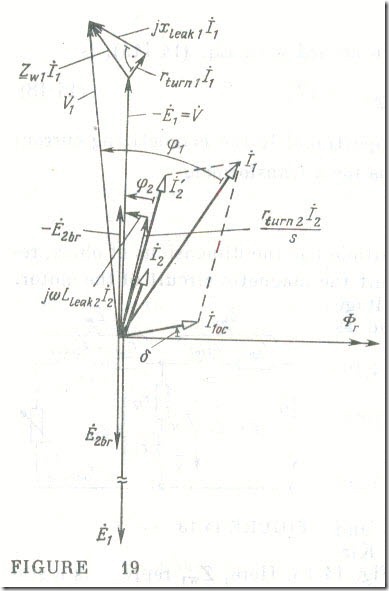

Under running conditions, the frequency of the current in the stator circuit is f and that of the current in the rotor circuit is f 2 = f s is, so no common phasor diagram may be constructed for the two circuits. However such a phasor diagram may be plotted if we assume an equivalent blocked rotor in the motor for which a model circuit representing one stator and rotor phase is shown in Fig. 19. This figure also shows the phasor diagram thus constructed and the phasor diagram for a stator phase carried over from Fig. 14 . unchanged . The reference vector is Φ̇r with respect to which the stator phase emf Ėl and the phase emf of the equivalent blocked rotor. Ė2,br , are in quadrature lagging .
With respect to - Ė2,br the rotor current İ2 lags behind by an angle
φ2 = arctan [(ɷLleak,2/(rw2+ r2)]
= arctan (sɷLleak,2/rw2)
which is the same phase difference as is observed between - Ė2 and İ2 when the rotor is revolving (see Fig 16) .
The secondary circuit includes a resistance
rw2 + r2 = rw2/s
and an inductive reactance ɷLleak.2 .Accordingly, Ė2,br consists of an active component, rw2 İ2/s , and a reactive component jɷLleak,2 İ2 .
The vector of the rotor phase current referred to the stator side is
İ'2 = (m2w2kw2/3wlkwl) İ2
and the stator phase current is
İ1 = İ'2 + İ1,nl
In the stator phase winding the referred current İ'2 corresponds to the rotor phase current İ2 which it compensates . The magnetizing current İ1,nl , which accounts for a part of the stator phase current, excites the revolving magnetic field of the motor. The magnetizing current phasor leads the magnetic flux phasor by an angle 6 owing to hysteresis and eddy-current losses in the core. The phasor diagram of one phase of an induction motor with its rotor blocked is in effect the same as the phasor diagram of a transformer (see Fig. 11).
The stator phase voltage phasor is plotted on the basis of the following equation:
V̇1 = - Ėl + rw1İ1+ jleak.1İ1
Labels: Electricity and Magnetism