The Power Rating and Efficiency of a Synchronous Generator
The power balance around a synchronous generator may be explained by reference to its phasor diagram (see Fig 4 b). By projecting the Ė0 phasor and its components onto the current phasor İ , we obtain the active component of the emf
E0 cos φ0 = rwI + V cos φ (15.5)
By multiplying Eq. (15.5) by the rms current I we transform Eq. (15.5) into an equation defining the power per phase of a synchronous generator
E0I cos φ0 = rwI 2 + VI cos φ (15.6)
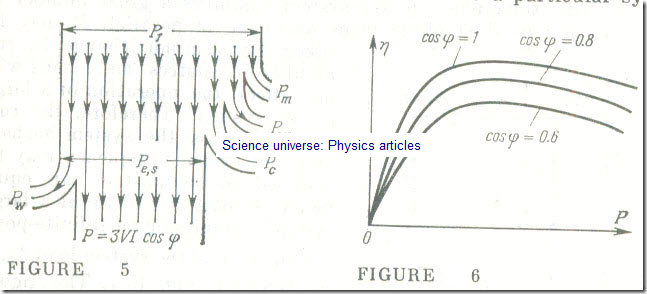
It shows that the electric power developed by the stator, Pe, s , is the sum of the power dissipated in the armature conductors, Pw, and the electric power, P, which the generator delivers to the line. In addition to the power dissipated in the conductors (traditionally called the copper loss), there is also the power lost mechanically (through windage and friction), Pm, and the power lost in the iron of the stator and pole shoes due to hysteresis and eddy-currents, collectively called the core (or iron) loss, Pc . As follows from Eq. (15.6), these losses are made up for not by electric power, but directly by the mechanical power coming from the associated prime mover. The overall power break-down is shown in Fig 5. There is also some power lost on field excitation. It is equal to the power delivered by a d.c. exciter, Pex, and accounts for about 0.3-1 % of the power rating of a large generator.
The total losses associated with a synchronous generator may be classed into fixed (or constant) losses which are nearly independent of load, and the variable loss which depends on load. The fixed losses, Pf1xed , is the sum of the mechanical losses, the excitation losses, and the core loss. The variable loss, Pvar is equal to the copper loss, that is, the power dissipated in the conductors.
Given the same current, the electric power of a synchronous generator, as expressed in terms of phase voltage and current, is
P = 3VI cos φ
and is a function of. the load power factor. However, the cross-sectional area of winding conductors is chosen for a particular value of current, whereas its insulation and the cross-sectional area of the magnetic circuit are chosen for a particular value of voltage. Hence, these quantities are chosen irrespective of the load power factor. For this reason, the power rating of a synchronous generator is defined, like that of a transformer, as
S = VI
and is expressed in kilovolt-amperes. It would be ill-advised to couple a synchronous generator to a turbine designed for its total power S (divided by its efficiency), because cos φ is less than unity nearly always. That is why the turbine chosen to drive a particular synchronous generator usually has a somewhat lower power rating than the total power of the generator (usually it is taken on the assumption
that cos φ = 0.8) .
The power output of a synchronous generator is proportional to its volume, so an increase in the power rating of a generator leads to a decrease in the cooling area per unit power and to a poorer cooling. To maintain proper cooling, one has to employ forced cooling and ventilation. In large turboalternators the quantity of air needed for ventilation is very large. The quantity of air expended to cool a generator every hour is about equal in weight to that of the machine itself.
For generators in sizes over 25 MVA it is usual to employ hydrogen cooling. Hydrogen cooling is more attractive because the weight of hydrogen is 1/14th that of air, its heat capacity is 14 times as great, its thermal conductivity is 7 times that of air, and the heat transfer per unit area is 1.35 times as great.
The efficiency of a synchronous generator is defined as the ratio of the power that the generator delivers to an electric network, to the power supplied by its prime mover. It is convenient to express the latter as the sum of the power output of the generator and all forms of power losses in the machine, that is,
η = 3VI cos φ/(3VI cos φ + Pflxed + Pvar) (15.7)
Equation (15.7) shows that a decrease in load leads to a decrease in efficiency. Plots of generator efficiency as a function of load for several values of the power factor appear in Fig 6. As the power rating of generators goes up, the efficiency of both the generator and of its prime mover improves.
Labels: Electricity and Magnetism