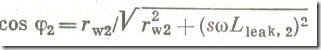
For an induction motor to run steadily, it is essential that its torque should balance the applied load automatically-as the load applied to the shaft of a motor is increased, the torque developed by the motor must go up in proportion. In a running induction motor, this condition of balance is achieved in the following way. As the load applied to the shaft is increased, the opposing torque exceeds the driving torque, the rotor slows down, and the slip goes up. This increase in the slip brings about an increase in the driving torque, and the two torques, driving and opposing, strike a balance at an increased slip.
The dependence of the driving torque on the slip is not so straightforward as it might appear from the foregoing, however. The point is that in Eq. (14.27) defining the driving torque of an induction motor, all the three quantities involved (I2, Φr, and cos φ) are functions of the slip. The rotor current 12 (see Sec. 14.7) increases rapidly with increasing slip due to the increase in E2 which is proportional to the slip. At first, so long as the leakage reactance of the rotor winding, sɷLleak,2, remains small in comparison with its resistance, rw2, the increase in the slip is accompanied by a rapid growth in the rotor current. Then, at sɷLleak,2 ≥ rW2 this growth in rotor current slows down.
The power factor of the rotor circuit
first decreases very slowly as the slip increases, then its decrease becomes more rapid. It seems useful to explain the physical conditions that govern the effect of cos φ2 on the driving torque. To this end, we assume the extreme ideal conditions. First we assume that cos φ2 = 0 or, which is the same, that the rotor winding only has an inductive reactance. In the circumstances, the rotor current would be a maximum in those of the rotor conductors where the induction was a maximum a quarter of a cycle previously (Fig 21). The current would be maximum where there is no induction associated with the rotating magnetic field, so the forces acting on the remaining rotor conductors cancel out one another and the driving torque at the shaft is zero.
In reality, the rotor circuit of an induction motor has both a resistance and an inductive reactance, with the latter varying in proportion to the slip so that the driving torque of the machine cannot but be affected.
The slip also affects the main flux, Φr , of the machine, although to a lesser degree. As the slip increases, the stator current I1 goes up, but the stator emf
Ė1 = V̇1 - Zwl İl
goes down, and so does Φr proportional to it, because, in accord with Eq. (14.10)
Φr = E1/4.44fwlkwl
In Eq. (14.27), three quantities are functions of the slip, with I2 increasing and with Φr and cos φ2 decreasing as the slip increases. Thus, there is what is known as the critical slip, Scr which corresponds to a maximum value of the driving torque.
In order to define the maximum driving torque in terms of the motor parameters, let us turn to Eq. (14.25) where 12 can be deduced from the equivalent circuit of a stator phase, Fig 19, on neglecting the no-load (open-circuit) current, I1,oc :
On taking the first derivative of Eq. (14.28) with respect to the slip and equating it to zero, we get
In Eq. (14.29), only the numerator may be equal to zero, so the critical slip corresponding to a maximum driving torque is
where the "-" sign applies when a machine is running as a generator. Since in actual machines r2w1 is never more than 5 % of the radicand, this term may be neglected. So the slip as expressed in terms of the rotor circuit parameters referred to the stator side will be
Scr = ± r'w2/(leak,1+ 'leak,2) (14.30)
On replacing r'w2 with krw2, 'leak,2 with kleak,2 and leak,1/k with ''leak,1 we obtain an expression for Scr in terms of the rotor winding resistance rw2, the rotor-winding leakage reactance kleak,2 and leak,1 which is the inductive leakage reactance of a stator phase winding referred to the number of phases, number of turns and winding coefficient of the rotor:
Scr = ± rw2/(''leak,1+ leak,2) (14.31)
The leakage inductance of the rotor windings is relatively large because the rotor conductors are placed in core slots. For this reason the maximum torque developed by an induction motor usually corresponds to fairly small values of slip, which is 4 % for large-size motors and up to 14 % for small-size motors.
A typical plot of the torque-vs-slip characteristics of an induction motor appears in Fig 22. The peak value of torque divides the plot into a stable region between S = 0 and Scr and an unstable region from Scr to S = 1 where the torque decreases with increasing slip.
In a running motor, a dynamic balance of the driving and load torques is maintained automatically with increasing slip so long as the opposing (load) torque remains smaller than the maximum torque developed by the motor. Once the load torque becomes equal to the maximum motor torque, any increase in the slip with a further increase in load will only lead to a decrease in the driving torque. In other words, the dynamic balance upset by an increase in load will no longer be restored and the motor will ultimately be brought to a stop by the prevailing load torque.
Now we will express the maximum driving torque in terms of the machine parameters. This can be done by substituting Eq, (14.30) into Eq. (14.28).
On neglecting rw1 in comparison with (leak,1+ 'leak,2) we obtain an expression for the maximum torque of an induction motor in the following simple form:
Tmax = (3p/2ɷ) V21/( leak,1+ 'leak,2 ) (14.32)
The maximum torque determines the overload capacity of an induction motor. Equation (14.32) shows that T max is independent. of the rotor-circuit resistance, whereas, as follows from Eqs. (14.30) and (14.31), the critical slip is proportional to that resistance. So, by increasing the resistance in the rotor circuit, we can raise the critical slip without causing any change in the maximum torque. This condition is utilized in order to improve the starting of wound rotor induction motors.
The fact that the maximum torque is proportional to V21makes induction motors very sensitive towards a fall in the supply-line voltage. If V1 happens to fall considerably, the motor may fail to start at all.
For conventional induction motors the maximum torque is 2-2.5 times the rated torque.
For purposes of electric drive, it is important to consider the speed-us-torque characteristic, n (T), of an induction motor. I t differs from the torque-slip curve only in that the coordinate axes are reversed.
As is seen from the torque-speed characteristic shown in Fig 23, the speed of an induction motor only slightly falls as the torque increases from zero to its maximum value-s-this is what is known as a flat speed-torque characteristic. When the load exceeds Tmax . (which occurs when the load is twice or three times the maximum torque), the motor enters an instability region (if the load applied to the shaft remains constant) and comes to a stop. For this reason, the power rating of a motor should be chosen so that a momentary overload could not exceed its maximum torque; otherwise the drive must be fitted with a flywheel.
The speed-torque characteristic applying to the normal operating conditions is called the natural speed-torque characteristic in contrast to that of a wound-rotor induction motor in which the rotor circuit contains a rheostat.
Labels: Electricity and Magnetism