
The kinematic equations of motion for constant acceleration, equation 2 1 and equations 2–3 through 2–6 of the previous chapter. can be applied to a large collection of problems known as “falling body problems,” problems where the constant acceleration is the acceleration due to gravity on the surface of the earth. These equations from the previous chapter are rewritten here for your convenience.
3 1 Consider a ball dropped from the top of a 40m tall building. Calculate everything possible. Solution: “Calculate everything possible” is an unusual request. Usually early in your study of falling body problems, there is a problem that asks for something that does not at all seem like it has anything to do with the information given. It's almost like asking “What color is the building?” When this happens, and it probably will, the way to do the problem is to calculate what you can and let the information you generate lead you through the problem. Let's apply this approach to this problem. First, diagram the problem as shown in Fig. 3 1. Place the origin at the top of the building with displacement, velocity, and acceleration (g) all positive down.
Since most of the kinematic equations contain the time, this is usually one of the first things to calculate. Use equation 3–4 to find the time for the ball to strike the ground.
Knowing the time we can calculate the velocity from equation 3-2.
Alternatively we can use equation 3–4.
NOTE: This last equation is a better one to use because it relies on original data rather than calculated data. If there had been an error in the time calculation it would have been repeated in the v = v0 + gt equation. Also round off errors are eliminated by using equations that rely on original data.
<><><><><><><><><><><><>
3 2 Now add a complication to problem 3 1 by throwing the ball down with an initial velocity of 8.0m/s. Find the time for the ball to reach the ground and the velocity on impact.
Solution: Again diagram the problem as in Fig. 3 2. Note that in this problem the displacement and velocity are positive down.
The time of flight is from 40m = (8.0m/s)tn + (1/2)(9.8m/s2)t2,
which rearranged and without units is 4.9t2 + 8.0t 40 = 0,
with solution by formula of
The positive time is the obvious choice.
The velocity at the ground level is from
<><><><><><><><><><><><>
3 3 Add a different complication to problem 3 1. Throw the ball up from the top of the building with a velocity of 8.0m/s. Find the time for the ball to reach the ground and the velocity on impact
Solution: Diagram the problem as in Fig. 3 3. Take x the displacement as positive down and the velocity as negative up. It is important to remember that the sign of the velocity is opposite that of the displacement. It doesn't matter whether the velocity is negative and the distance down positive or vice versa. It does matter that the signs be opposite! Getting a sign wrong is the source of many, possibly most, errors in falling body problems.
Calculate the time of flight and note the signs:
Rearranging and without units, this equation is 4.9t2 8.0t 40 = 0,
with solution
The positive time is the obvious choice. Note the numbers used for the solutions to the quadratics in time for this and problem 3 2.
The velocity when the ball strikes the ground is
Notice that whether the v term is a positive or negative number, the result is the same. If the ball is thrown up with a certain velocity or down with the same velocity, the velocity at impact is the same. This is to be expected from the symmetry of the equations. If the ball is thrown up with a certain velocity, then on the way down it passes the same level (from which it was thrown) with (numerically) that same velocity.
3–4 For the situation of problem 3 3 calculate the maximum height above the top of the building and the time for the ball to reach maximum height.
Solution: The time for the ball to reach maximum height is from equation 3 2. Note that at maximum height the velocity must be zero. Again watch the signs closely. It doesn't matter how you choose the signs, but the acceleration has to be opposite the velocity. The equations
yield the same result, t = 0.82s. Because of symmetry, it takes the ball the same amount of time to reach maximum height as it does for the ball to return to the original level. Calculate the height above the top of the building from equation 3–5.
A thorough understanding of these four problems will keep you from making sign mistakes in problems like these.
<><><><><><><><><><><><>
3–5 A bottle of champagne is dropped by a balloonist. The balloon is rising at a constant velocity of 3.0m/s. It takes 8.0s for the bottle of champagne to reach the ground. Find the height of the balloon when the bottle was dropped, the height of the balloon when the bottle reached the ground, and the velocity with which the bottle strikes the ground.
Solution: Diagram the situation as shown in Fig. 3–4 being especially careful about the relative orientation (algebraic signs) of displacement, velocity, and acceleration. There are several possibilities as regards the origin and direction of the coordinate system. Take the origin at the height of the balloon when the bottle is dropped; the position of the balloon at t = 0. Take the displacement as positive down. The main reason for taking the displacement as positive down is that the acceleration is down and the initial velocity up making two positives and one negative. As time goes on, however, displacement, velocity, and acceleration will be positive. This choice seems to make for fewer minus signs and less chance for error with an algebraic sign.
Write the equation for the height of the balloon (when the bottle was dropped) counting time from when the bottle was dropped
The height of the balloon when the bottle reached the ground would be the height when the bottle was dropped plus the amount the balloon rose in the 8.0s it took the bottle to reach the ground, or 290m + (3.0m/s)8.0s = 314m
The velocity on impact v = v0 + at = 3.0m/s + (9.8m/s2)8.0s = 75m/s.
This velocity could also be calculated using
3–6 A parachutist descending at a constant rate of 2.0m/s drops a smoke canister at a height of 300m. Find the time for the smoke canister to reach the ground and its velocity when it strikes the ground. Then find the time for the parachutist to reach the ground, the position of the parachutist when the smoke canister strikes the ground, and an expression for the distance between the smoke canister and the parachutist.
Solution: Diagram the system as shown in Fig. 3–5 taking displacement, velocity, and acceleration as positive down with the origin at the point where the canister is dropped.
The time for the smoke canister to reach the ground is from equation 3–4.
Without units the equation is 4.9t2 + 2.0t 300 = 0 with solutions
The time for the canister to reach the ground is 7.6s.
The velocity when it strikes the ground is
The time for the parachutist to reach the ground is from equation 3 2.
When the canister strikes the ground the parachutist has dropped (2.0m/s)7.6s = 15m and is 285m above the ground.
The expression for the distance between the canister and the parachutist is
3–7 A coconut is dropped from a height of 60m. One second later a second coconut is thrown down with an initial velocity. Both coconuts reach the ground at the same time. What was the initial velocity of the second coconut?
Solution: In problems where there is a time delay it is usually best to calculate the position, velocity, and acceleration of the first particle at the time when the second particle starts to move. In the train problem in the previous chapter there was a position difference between the two trains at t = 0 that was easily translated into the equations. It is possible to do time delay problems with a time differential in one set of equations. The difficulty with this approach is that it is easy to get an algebraic sign wrong. If you say that the time for the second particle is the time for the first plus the difference between them, then it is essential that the algebraic sign of the difference be correct. It is much easier, especially when you are learning how to do problems with a time delay, to do them in this slower, but inherently more accurate, method. First, calculate the state of the first particle when the second one begins moving. Then, write the two sets of equations describing the motion with this instant as t = 0.
Calculate the position and velocity of the first coconut at the end of one second, the time when the second one starts.
Since everything (position, velocity, and acceleration) is positive down, orient the coordinate system for positive down with the origin at the top. Now diagram the problem as in Fig. 3–6. At the instant the second coconut is thrown down, the first coconut has position 4.9m, velocity 9.8m/s and acceleration 9.8m s2.
Since both coconuts strike the ground at the same time use the conditions of the first coconut to find the total time.
First calculate the velocity at impact of the first coconut.
The time for the second coconut to reach the ground is the same as the time for the first coconut to go from 4.9m to 60m or the time for the first coconut to go from 9.8m/s to 34.3m/s.
This comes from v = v0 + at. where v0 is v10, the velocity of the first coconut when the second one is thrown down, and v is the velocity of the first coconut at the ground.
Now that we have the time for the second coconut to travel the 60m we can find its initial velocity from x x0 = v20t + (1/2) at2 where t is the total time for the second coconut.
Review this problem until all the different times and velocities are clear in your mind. Set up the problem and do it yourself without reference and you will know you understand it.
3–8 A boat is passing under a bridge. The deck of the boat is 15m below the bridge. A small package is to be dropped from the bridge onto the deck of the boat when the boat is 25m from just below the drop point. What (boat) speed is necessary to have the package land in the boat?
Solution: Calculate the time for the package to fall the 15.0m using
The boat must move at 25m/1.7s = 14m/s
3–9 You are observing steel balls falling at a constant velocity in a liquid filled tank. The window you are using is one meter high and the bottom of the window is twelve meters from the bottom of the tank. You observe a ball falling past the window taking 3.0s to pass the window. Calculate the time required to reach the bottom of the tank, after the ball has reached the bottom of the window..
Solution: The situation is diagrammed in Fig. 3–7.
The observed velocity is 1.0m/3.0s so 12m = (1.0m/3.0s)t or t = 36s
3–10 In a situation similar to problem 3–9, the tank is filled with a different liquid causing the acceleration in the tank to be 6.0m/s2 and the time to traverse the window, 0.40s. Calculate the height of the liquid above the window, the time to reach the bottom of the tank, and the velocity of the ball when it reaches the bottom of the tank.
Solution: Diagram the problem as in Fig. 3–8.
From the data about the window, calculate the velocity of the ball at the top of the window.
The velocity at the bottom of the window is from
The time to reach the bottom of the tank is from x - x0 = vbt + (1/2)at2
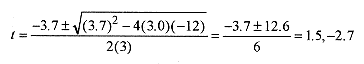
This (positive) time is for the ball to travel from the bottom of the window to the bottom of the tank.
Assuming the ball started at zero velocity the distance from the top of the liquid to the top of the window, xt,
Solution: Diagram the problem as in Fig. 3–9. This is another example of a question that seems totally unrelated to the information in the problem. When you don't know where to start, and you do not see a clear path to the desired answer, simply start where you can, calculating what you can and hopefully learning enough to answer the specific question.
Fig. 3–9
One of the first things we can calculate in this problem is the average velocity at the middle of the window.
This average velocity is the velocity of the ball on the way up (and on the way down) at the middle of the window. Add this feature to the problem. With this information we can usto find the distance the ball rises above the midpoint of the window.
So the ball rises 2.5 0.7 = 1.8m above the top of the window.
Second Solution: View the ball as decelerating as it goes up past the window and find vb at the bottom of the window from .
Velocity and displacement are taken as positive so acceleration is negative.
Now the distance to maximum height (velocity zero) is
Again the maximum height of the ball above the top of the window is 3.2m 1.4m = 1.8m.
Labels: How To Solve Physics Problems