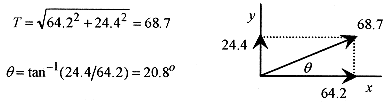Vectors
This chapter serves a dual purpose. First, it will help you to do the addition and subtraction of vectors in the chapter in your text on vectors and the vector problems in the chapters on motion and forces. Second, it will serve as a reference for those topics involving vector products, especially the definitions of work and torque encountered in mechanics.
Certain physical quantities such as mass or temperature are described with a number called a scalar. Other quantities, such as displacement, velocity, or force, have a direction associated with them and are called vectors. Operationally, a vector is an arrow oriented in space with the length (of the arrow) representing the number and the orientation, the direction. Vectors can be placed anywhere on a coordinate system so long as they maintain their required length and orientation.
Number Plus Angle and Components
A vector can be described with a number and an angle as A = 23<37°. In performing the basic mathematical operations of addition, subtraction, multiplication, and division, it is more convenient to write vectors in component form. If A were placed with the tail (of the vector) at the origin of a coordinate system, then the x and y components could be written as shown in Fig. 1 1.
It is very important in the use of vectors to be able to go from the number plus angle format to component format quickly and accurately. Before going any further in this chapter review the basic trigonometric relations and the formulas for going from number plus angle to components and vice versa (Fig. 1–2). And if you are at all unsure of yourself make up a 3 × 5 card with figure and formulas and review it several times a day until you can perform the operations without hesitation.
A vector A = A <0 has components as shown in Fig. 1–2. (The bold type represents the vector, and the normal type represents the number associated with that vector.) If the components, ax and ay, are given, then the number plus angle form can be obtained with the trigonometric relations on the left side of Fig. 1–2.
The vector A (see Fig. 1-1) can be reconstructed from the components ax = 18.4 and ay = 13.8.
1 -1 Diagram the vector C = 47<193° and write the components.
Solution: The components are cx = 47 cos193° = 45.8 and cy = 47 sin 193° = 10.6.
Taking the sine or cosine of the 193° angle will produce the appropriate negative numbers, but drawing a figure and using the principle angle is a better procedure. Less mistakes are made from figures than from the readout of calculators. When the vector and its components are drawn on the coordinate system there can be no mistake that 45.8 and 10.6 are both negative.
Unit Vectors in Two Dimensions
The use of unit vectors simplifies the mathematical operations on vectors. In two dimensions unit vectors are vectors of unit value directed in the +x and +y directions.
The vector A (Fig. 1 1) would be written as A = 18.4i + 13.8j and C (problem 1 1) would be written as C = 45.8i 10.6j
1–2 Add the vectors A and C.
Solution: The addition of A and C is now accomplished by adding the components
Solution:
1–4 Diagram T = A–C and write in number plus angle form.
Solution: The diagram is started by drawing the components on the coordinate system. With the components the magnitude and angle can be calculated T = 68.7<20.8°.
1–5 Add the vectors A = 13<50°, B = 15< 60°, and C = 17<20°.
Solution: Diagram each vector along with the components.
The sum of these vectors R = A + B + C is R = 1.2i–11.5j. This resultant vector is diagrammed in Fig. 1–7 along with the magnitude and angle.
The vector is R = 11.6< 84°
The key to getting vector addition problems correct is to use multiple diagrams. Most mistakes in vector problems are sign mistakes. And the way to avoid sign mistakes is to use diagrams extensively.
1–6 Find the resultant of the two forces F1 = 800N<47° and F2 = 600N<140°.
Solution: Place the force vectors with components on the same diagram (Fig. 1–8).
The components of the resultant can be diagrammed directly. If the diagrams are done in this manner it is not necessary to use large angles and misread calculator readouts. Note that component forces in the y direction are both positive, while F1x and F2x are in opposite directions. Taking forces acting in the +x and +y directions as positive, and forces acting in the x and y directions as negative, the result of the addition of these two forces is 86 in the +x direction and 971 in the +y direction. Using the diagram it is not necessary to keep track of the plus and minus signs. The diagram makes clear how the components should be added to produce the correct resultant. The resultant written in magnitude and angle form F = 975N<85°
There are two different types of products of vectors. One results in a scalar, and the other results in a vector. The next two sections discuss these products. Depending on the order of topics in your course, you may want to put off reading these sections until they come up in mechanics.
Scalar or Dot Product
The dot product (A .B) produces a scalar. There are two definitions of the dot product. The most easily visualized is
where è is the angle between A and B. This definition can be viewed as the projection of A on B or the component of A in the direction of B times the magnitude of B.
The second definition fits with the unit vector notation
Following A.B = AB cosè, i.i = 1.1 cos0=1° = 1, and i.j = 1.1cos90° = 0.
Following A.B = axbx + ayby, i.i = 1.1, and i.j = 0.
1–7 Form the dot product of A = 23<37° and B = 14< 35°.
Solution: Using the first definition A . B = A . B cosè= 23.14 cos72° = 100.
The second definition of the dot product requires the components of the vectors. The components of A (from Fig. 1 1) are ax = 18.4 and ay = 13.8. The components of B are in Fig. 1–11.
The dot product is
More dot product problems will be done in the chapters where dot products are used in the calculation of work. Work, as defined in mechanics, is the product of the component of an applied force in the direction of a displacement and that displacement. W = F.s
The cross product (A ~ B) produces a vector. As with the dot product there are two definitions of the cross product. The simplest definition to understand is that the cross product of A and B produces a vector of magnitude AB sin ƒÓ in a direction normal (perpendicular) to the plane of A and B with ƒÓ the angle between A and B. The specific direction is obtained by rotating A into B (crossing A into B or A cross B) again using the fingers of the right hand naturally curling (closing) from A to B with the thumb pointing in the direction of the new (product) vector. This is the same procedure as for finding the z direction in an x y z right handed coordinate system. A right handed coordinate system with the three unit vectors is shown in Fig. 1.12.
Practice visualizing i ~ j to produce k and j ~ k to produce i. The angle between the unit vectors is 90‹, and their magnitude is 1; so the resultant vector has magnitude 1 and is in the direction given by this gvector crossed into another vectorh procedure. Practice pointing your fingers in the direction of the first vector, curling them into the second vector with your thumb pointing in the direction of the result of this gcrossh product until you can quickly see that i ~ k = j and k ~ i = +j.
The definition of torque in mechanics is lever arm times force times the sine of the angle between them. Another way of saying this is that torque is lever arm times the component of the force at right angles to the lever arm. In mathematical terms
with the magnitude of the torque given by T = rF sin Į and the direction of the vector given by the r ~ F role. The F sin Į term can be viewed as the component of F perpendicular to r.
In Fig. 1.13 the vectors are arranged as the sides of a parallelogram with F sin Į the height of the parallelogram. The product rF sin Į is the magnitude of r ~ F and is also the area of the parallelogram (a base times the height) formed by r and F.
The second definition of the cross product is mathematically easier but harder to relate to physical problems. This definition is expressed as a determinant.
1–8 Form the cross product of A = 23<37° and C = 47 <193°.
Solution: The vectors and their components are shown in Fig. 1–14. Crossing A into C defines the angle as 156° so that AC sin 156° = 440 with the direction out of the paper as give by the right hand rule.
Doing the same problem with determinants
The numeric difference, 440 versus 437, is due to rounding the components to three significant figures.
In simple problems it is easier to find the cross product from the geometric definition. In more complicated problems, or where it is difficult to be sure of the direction of the vector product, the determinant form is more convenient.