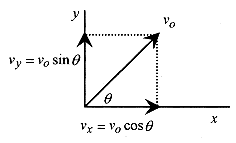
In order to understand projectile motion you have to look at the motion in two directions with one direction oriented in the direction of constant acceleration and the other direction at a right angle to it so as to form an x y coordinate system. In most problems, where an initial velocity and angle with the horizontal is given, the velocity is written in component form.
Fig.4 1
Note that the motion is effectively separated into horizontal and vertical components (one in the direction of the constant acceleration and one at a right angle to the acceleration).
The motion is a parabola in this coordinate system. The symmetry of parabolas (in this case parabolic motion) is helpful in understanding the motion. (See the Introduction, Mathematical Background, for a discussion of the properties of parabolas.) In order to better understand how the motion is separated and how the parabolic property helps us to understand projectile problems we will do a simple problem without numbers just to get a feel for the features of the motion. If you are familiar with the properties of parabolas you may want to skip this discussion and go directly to the worked problems.
In Fig. 4 1 the velocity of the projectile is written in component form. The acceleration in the horizontal direction is zero and in the vertical direction is due to gravity. With the velocity components, and the acceleration in the direction of an axis, we can write the six equations describing acceleration, velocity, and position in the x and y directions.
These equations are based on the kinematic equations of motion for constant acceleration:
The six equations are:
The equations for x and y can be looked upon as parametric equations in time. Parametric equations such as x = f(t) and y = f (t) are equations that can be combined to produce y = f (x) or x = f (y). To find the position of the particle in x–y, or y as a function of x, solve one equation for t and substitute into the other. In this case solve x=… for t, as this is the simplest choice.
Substitute into y = … to obtai
This is of the form y = ax2 + bx = x( ax+b), which is a parabola that opens down and intercepts the y axis (makes y = 0) at x = b/a.
The range, or value of xwhen y = 0, can be determined from the factored form of this equation
which tells us that y = 0 at x = 0 and
or using the trigonometric identity 2sinθcosθ=sin2θ
The maximum range occurs for an angle of 45°, corresponding to sin 2è= 1.
The main point of this discussion is that the motion is a parabola, and the properties of parabolas can be used in solving problems in projectile motion. That the maximum range occurs at 45° is not surprising, and is generally not of interest in problems.
The expression for maximum range is only of passing interest, since the range is one of the easier things to calculate in any problem. Do not consume precious memory space memorizing formulas for the range or time of flight. If you work the problems by first writing down the six equations describing the motion, then the time of flight, range, and many other things are easily calculated.
In order to set up a problem in projectile motion, first orient one axis of a right angle (x–y) coordinate system in the direction of constant acceleration. Remember to place the origin of the coordinate system and the positive direction for x and y for (your) convenience in solving the problems. Then write equations for acceleration, velocity, and position for each direction. Along with the symmetry of the motion, these equations can be used to find the characteristics (position, velocity, and acceleration) of the projectile at any point in space or time. The procedure is illustrated with a simple problem.
4 1 A soccer player kicks a ball at an initial velocity of 18m/s at an angle of 36° to the horizontal. Find the time of flight, range, maximum height, and velocity components at t = 0, mid range, and at impact.
Solution: The acceleration is down so set up the coordinate system with x horizontal (along the ground ) and y vertical, and place v0 on the graph. Write the velocity in component form, and calculate vx0 and vy0.
Now, and this and this is the key to getting the problem right, write down the six equations governing the motion starting with the accelerations (the accelerations are the easiest to write).
Now look at the motion, which is parabolic in x–y, keeping in mind the properties of parabolas.
Fig.4 3
The ball is on the ground at t = 0 and t = ô, the time of flight. To find these times, set y = 0 and obtain (without units)
which gives t = 0 and t = 10.6/4.9 = 2.16s, the time of flight.
The range is the value of x at 2.16s:
The maximum height, and vy = 0, occur at 1.08s (one half the time of flight). Therefore the maximum height is y at t = 1.08s
The procedure for doing the problem is to write the initial velocity in component form, write the six equations for acceleration, velocity, and position, and then perform the mathematical operations answering questions about the problem.
4 2 For the situation of problem 4 1 suppose the field is covered with fog down to 3.0m above the ground. What are the times for the ball's entry into and exit out of the fog?
Solution: The times are found from the equation for y as a function of time with y set equal to 3.0m.
As an exercise find the x positions for these times.
<><><><><><><><><><><><>
4 3 An airplane traveling at 100m/s drops a bomb from a height of 1500m. Find the time of flight, distance traveled, and the velocity components as the bomb strikes the ground.
Solution: Start by placing the origin of the coordinate system at the point where the bomb is released. And take the direction the bomb falls due to gravity as positive x and the horizontal position as y. This is different from the conventional orientation, but it is convenient in this problem because the six equations all come out positive!
Now write down the six equations governing the motion.
With these six equations we can answer all the questions in the problem. We need only to “translate” the word questions into algebra questions.
a) The time for the bomb to reach the earth means: Find the time when x = 1500m?
b) How far does the bomb travel horizontally means: Find the value of y when t = 17 s?
c) Find the velocity components at impact means: Find vx and vy at t = 17s?
d) Where is the airplane when the bomb strikes the earth means: What is y and t = 17 s?
Remember that the plane and the bomb have the same velocity in the horizontal direction.
<><><><><><><><><><><><>
4 4 A baseball is hit at a 45° angle and a height of 0.90m. The ball travels a total distance of 120m. What is the initial velocity of the ball? What is the height of the ball above a 3.0m fence 100m from where the ball is hit?
Solution: This problem is unique in that it requests the initial velocity, a number usually given in the problem. Also note that the angle is 45°, the angle for maximum range. The other interesting feature of the problem is the question concerning the height at some specific point down range. Set up the problem in the conventional way assigning v0 to the initial velocity.
The next question is how to handle the ball being hit at 0.90m above the ground. Since v0 is specified at the point where the ball is hit, and this is where we start counting time, then the origin for the coordinate system should be put here. We just need to keep in mind that this origin is 0.90m above the ground level.
Now write the six equations.
The first question reduces to finding vo for the 120m hit. Algebraically this means that when y = 0.9m, x = 120m, so write the two equations (for x and y) with these conditions
Note that so write
This is the time of flight, so put this time into the equation for x.
The next part of the problem asks for the height above the fence at 100m. Again we need to find the time for x to be 100m down range and substitute this value of t into the y equation
This is the time for the ball to go 100m. The height of the ball at this time is
Remember that this is 15.6m above the zero of the coordinate system which is 0.90m above the ground. So the ball is 16.5m above the ground at this point and for a 3.0m high fence is 13.5m above the fence.
<><><><><><><><><><><><>
4–5 A physicist turned motorcycle stunt rider will jump a 20m wide row of cars. The launch ramp is 30° and 9.0m high. The land ramp is also 30° and is 6.0m high. Find the minimum speed for the launch.
Solution:
Fig. 4–7
First write down the six equations of motion.
The minimum v0 is dictated by the condition that the rider be at x = 20m and y = 3.0m. So put these conditions into the equations for x and y.
At this point we can solve for v0 by substituting
from the first equation into the second equation.
This is the minimum velocity to make the jump.
As a follow on to this problem calculate the velocity to just hit the end of the ramp. This velocity gives an upper limit to the jump velocity.
<><><><><><><><><><><><>
Go back through the problems and notice the common approach:
1) orient a coordinate system,
2) write the six equations of motion, and
3) translate the word questions into algebra.
In these problems we have not always used each of the six equations to answer the question. Few problems require the detailed description of the motion available in the six equations. If, however, each problem is described by these six equations you will always have all the information to answer any possible question about the motion.
Labels: How To Solve Physics Problems