Basic Principles
Thermodynamics involves the storage, transformation, and transfer of energy. Energy is stored as internal energy (due to temperature), kinetic energy (due to motion), potential energy (due to elevation), and chemical energy (due to chemical composition); it is transformed from one of these forms to another; and it is transferred across a boundary as either heat or work. We will present equations that relate the transformations and transfers of energy to properties such as temperature, pressure, and density. The properties of materials thus become very important. Many equations will be based on experimental observations that have been presented as mathematical statements, or laws: primarily the first and second laws of thermodynamics.
The mechanical engineer’s objective in studying thermodynamics is most often the analysis of a rather complicated device, such as an air conditioner, an engine, or a power plant. As the fluid flows through such a device, it is assumed to be a continuum in which there are measurable quantities such as pressure, temperature, and velocity. This book, then, will be restricted to macroscopic or engineering thermo- dynamics. If the behavior of individual molecules is important, statistical thermo- dynamics must be consulted.
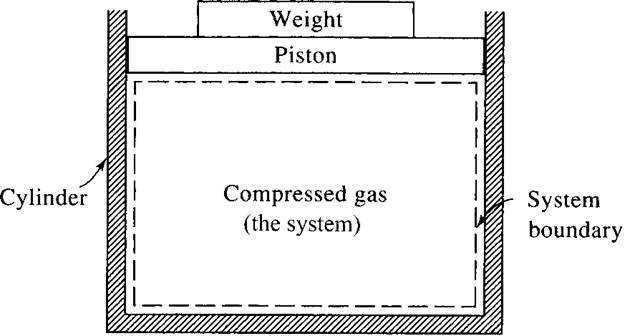
A thermodynamic system is a fixed quantity of matter upon which attention is focused. The system surface is one like that surrounding the gas in the cylinder of Fig. 1.1; it may also be an imagined boundary like the deforming boundary of a certain amount of water as it flows through a pump. In Fig. 1.1 the system is the compressed gas, the working fluid, and the dashed line shows the system boundary.
All matter and space external to a system is its surroundings. Thermodynamics is concerned with the interactions of a system and its surroundings, or one system interacting with another. A system interacts with its surroundings by transferring energy across its boundary. No material crosses the boundary of a system. If the system does not exchange energy with the surroundings, it is an isolated system.
An analysis can often be simplified if attention is focused on a particular volume in space into which, and/or from which, a substance flows. Such a volume is a control volume. A pump and a deflating balloon are examples of control volumes. The surface that completely surrounds the control volume is called a control surface. An example is sketched in Fig. 1.2.
Figure 1.1 A system.
In a particular problem we must decide whether a system is to be considered or whether a control volume is more useful. If there is mass flux across a boundary, then a control volume is usually selected; otherwise, a system is identified. First, systems will be considered followed by the analysis of control volumes.
In engineering thermodynamics we postulate that the material in our system or control volume is a continuum; that is, it is continuously distributed throughout the region of interest. Such a postulate allows us to describe a system or control volume using only a few measurable properties.
Consider the definition of density given by
where Δ m is the mass contained in the volume ΔV, shown in Fig. 1.3. Physically, ΔV cannot be allowed to shrink to zero since, if ΔV became extremely small, Δ m would vary discontinuously, depending on the number of molecules in ΔV.
There are, however, situations where the continuum assumption is not valid; for
example, the re-entry of satellites. At an elevation of 100 km the mean free path, the average distance a molecule travels before it collides with another molecule, is about 30 mm; the macroscopic approach with its continuum assumption is already questionable. At 150 km the mean free path exceeds 3 m, which is comparable to the dimensions of the satellite! Under these conditions, statistical methods based on molecular activity must be used.
1.3 Properties and State of a System
The matter in a system may exist in several phases: a solid, a liquid, or a gas. A phase is a quantity of matter that has the same chemical composition throughout; that is, it is homogeneous. It is all solid, all liquid, or all gas. Phase boundaries separate the phases in what, when taken as a whole, is called a mixture. Gases can be mixed in any ratio to form a single phase. Two liquids that are miscible form a mixture when mixed; but liquids that are not miscible, such as water and oil, form two phases.
A pure substance is uniform in chemical composition. It may exist in more than one phase, such as ice, liquid water, and vapor, in which each phase would have the same composition. A uniform mixture of gases is a pure substance as long as it does not react chemically (as in combustion) or liquefy in which case the composition would change.
A property is any quantity that serves to describe a system. The state of a system is its condition as described by giving values to its properties at a particular instant. The common properties are pressure, temperature, volume, velocity, and position; others must occasionally be considered. Shape is important when surface effects are significant.
The essential feature of a property is that it has a unique value when a system is in a particular state, and this value does not depend on the previous states that the system passed through; that is, it is not a path function. Since a property is not dependent on the path, any change depends only on the initial and final states of the system. Using the symbol f to represent a property, the mathematical statement is
This requires that df be an exact differential; f2 – f1 represents the change in the property as the system changes from state 1 to state 2. There are several quantities that we will encounter, such as work, that are path functions for which an exact differential does not exist.
A relatively small number of independent properties suffice to fix all other properties and thus the state of the system. If the system is composed of a single phase, free from magnetic, electrical, and surface effects, the state is fixed when any two properties are fixed; this simple system receives most attention in engineering thermodynamics.
Thermodynamic properties are divided into two general types, intensive and extensive. An intensive property is one that does not depend on the mass of the system. Temperature, pressure, density, and velocity are examples since they are the same for the entire system, or for parts of the system. If we bring two systems together, intensive properties are not summed.
An extensive property is one that does depend on the mass of the system; mass, volume, momentum, and kinetic energy are examples. If two systems are brought together the extensive property of the new system is the sum of the extensive properties of the original two systems.
If we divide an extensive property by the mass, a specific property results. The
specific volume is thus defined to be
We will generally use an uppercase letter to represent an extensive property (exception: m for mass) and a lowercase letter to denote the associated intensive property.
When the temperature of a system is referred to, it is assumed that all points of the system have the same, or approximately the same, temperature. When the proper- ties are constant from point to point and when there is no tendency for change with time, a condition of thermodynamic equilibrium exists. If the temperature, for example, is suddenly increased at some part of the system boundary, spontaneous redistribution is assumed to occur until all parts of the system are at the same increased temperature.
If a system would undergo a large change in its properties when subjected to some small disturbance, it is said to be in metastable equilibrium. A mixture of gasoline and air, and a bowling ball on top of a pyramid are examples.
When a system changes from one equilibrium state to another, the path of successive states through which the system passes is called a process. If, in the passing from one state to the next, the deviation from equilibrium is small, and thus negligible, a quasiequilibrium process occurs; in this case, each state in the process can be idealized as an equilibrium state. Quasiequilibrium processes can approximate many processes, such as the compression and expansion of gases in an internal combustion engine, with acceptable accuracy. If a system undergoes a quasiequilibrium process (such as the compression of air in a cylinder of an engine) it may be sketched on appropriate coordinates by using a solid line, as shown between states 1 and 2 in Fig. 1.4a. If the system, however, goes from one equilibrium state to another through a series of nonequilibrium states (as in combustion) a nonequilibrium process occurs. In Fig. 1.4b the dashed curve represents a nonequilibrium process between (V1, P1) and (V , P ); properties are not uniform throughout the system and thus the state of the system is not known at each state between the two end states.
Whether a particular process may be considered quasiequilibrium or nonequilibrium depends on how the process is carried out. Let us add the weight W to the piston of Fig. 1.5 and explain how W can be added in a nonequilibrium manner or in an equilibrium manner. If the weight is added suddenly as one large weight, as in Fig. 1.5a, a nonequilibrium process will occur in the gas. If we divide the weight into a large number of small weights and add them one at a time, as in Fig. 1.5b, a quasiequilibrium process will occur.
Note that the surroundings play no part in the notion of equilibrium. It is possible that the surroundings do work on the system via friction; for quasiequilibrium it is only required that the properties of the system be uniform at any instant during a process.
When a system in a given initial state experiences a series of quasiequilibrium pro- cesses and returns to the initial state, the system undergoes a cycle. At the end of the cycle the properties of the system have the same values they had at the beginning.
Figure 1.5 (a) Equilibrium and (b) nonequilibrium additions of weight.
The prefix iso- is attached to the name of any property that remains unchanged in a process. An isothermal process is one in which the temperature is held constant; in an isobaric process, the pressure remains constant; an isometric process is a constant-volume process. Note the isobaric and the isometric legs in Fig. 1.6 (the lines between states 4 and 1 and between 2 and 3, respectively).
While the student is undoubtedly comfortable using SI units, much of the data gathered and available for use in the United States is in English units. Table 1.1 lists units and conversions for many thermodynamic quantities. Observe the use of V for both volume and velocity. Appendix A presents the conversions for numerous additional quantities.
When expressing a quantity in SI units, certain letter prefixes shown in Table 1.2 may be used to represent multiplication by a power of 10. So, rather than writing 30 000 W (commas are not used in the SI system) or 30 × 103 W, we may simply write 30 kW.
The units of various quantities are interrelated via the physical laws obeyed by the quantities. It follows that, no matter the system used, all units may be expressed as algebraic combinations of a selected set of base units. There are seven base units in the SI system: m, kg, s, K, mol (mole), A (ampere), cd (candela). The last one is rarely encountered in engineering thermodynamics. Note that N (newton) is not listed as a base unit. It is related to the other units by Newton’s second law,
F = ma (1.4)
If we measure F in newtons, m in kg, and a in m/s2, we see that N = kg . m/s2. So, the newton is expressed in terms of the base units.
Table 1.1 Conversion Factors
| Quantity | Symbol | SI Units | English Units | To Convert from English to SI Units Multiply by |
| Length | L | m | ft | 0.3048 |
| Mass | m | kg | lbm | 0.4536 |
| Time | t | s | sec | 1 |
| Area | A | m2 | ft2 | 0.09290 |
| Volume | V | m3 | ft3 | 0.02832 |
| Velocity | V | m/s | ft/sec | 0.3048 |
| Acceleration | a | m/s2 | ft/sec2 | 0.3048 |
| Angular velocity | w | rad/s | rad/sec | 1 |
| Force, Weight | F, W | N | lbf | 4.448 |
| Density | r | kg/m3 | lbm/ft3 | 16.02 |
| Specific weight | g | N/m3 | lbf/ft3 | 157.1 |
| Pressure | P | kPa | psi | 6.895 |
| Work, Energy | W, E, U | J | ft · lbf | 1.356 |
| Heat transfer | Q | J | Btu | 1055 |
| Power | . W | W | ft · lbf/sec | 1.356 |
| W | hp | 746 | ||
| Heat flux | . Q | J/s | Btu/sec | 1055 |
| Mass flux | . m | kg/s | lbm/sec | 0.4536 |
| Flow rate | . V | m3/s | ft3/sec | 0.02832 |
| Specific heat | C | kJ/kg ·K | Btu/lbm · R | 4.187 |
| Specific enthalpy | h | kJ/kg | Btu/lbm | 2.326 |
| Specific entropy | s | kJ/kg ·K | Btu/lbm · R | 4.187 |
| Specific volume | v | m3/kg | ft3/lbm | 0.06242 |
Weight is the force of gravity; by Newton’s second law,
W = mg (1.5)
Since mass remains constant, the variation of W is due to the change in the acceleration of gravity g (from about 9.77 m/s2 on the highest mountain to 9.83 m/s2 in the deepest ocean trench, only about a 0.3% variation from 9.80 m/s2). We will use the standard sea-level value of 9.81 m/s2 (32.2 ft/sec2), unless otherwise stated.
Table 1.2 Prefixes for SI Units
| Multiplication Factor | Prefix | Symbol |
| 1012 | tera | T |
| 109 | giga | G |
| 106 | mega | M |
| 103 | kilo | k |
| 10–2 | centi* | c |
| 10–3 | mili | m |
| 10–6 | micro | m |
| 10–9 | nano | n |
| 10–12 | pico | p |
*Discouraged except in cm, cm2, or cm3.
EXAMPLE 1.1
Express the energy unit J (joule) in terms of the base units.
Solution
The units are related by recalling that energy is force times distance:
We used Newton’s second law to relate newtons to the base units.
EXAMPLE 1.2
Express the kinetic energy mV 2/2 in acceptable terms if m = 10 kg and V = 5 m/s.
Solution
Labels: Thermodynamics