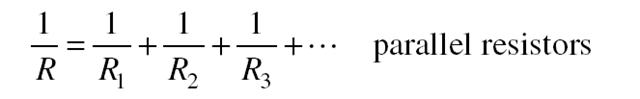
Direct-Current Circuits: Resistors in Series , Resistors in Parallel , EMF and Internal Resistance and Kirchhoff ’s Rules

Direct-Current Circuits

In This Chapter:

✔ Resistors in Series

✔ Resistors in Parallel

✔ EMF and Internal Resistance

✔ Kirchhoff ’s Rules

Resistors in Series

The equivalent resistance of a set of resistors depends on the way in which they are connected as well as on their values. If the resistors are joined in series, that is, consecutively (Figure 13-1), the equivalent resistance R of the combination is the sum of the individual resistances:

R = R1 + R2 + R3 + L+……     series resistors

Resistors in Parallel

In a parallel set of resistors, the corresponding terminals of the resistors are connected (Figure 13-2). The reciprocal 1/R of the equivalent resistance of the combination is the sum of the reciprocals of the individual resistances:

If only two resistors are connected in parallel,

Solution. Figure 13-3(b) shows how the original circuit is decomposed into its series and parallel parts, each of which is treated in turn. The equivalent resistance of R1 and R2 is

This equivalent resistance is in series with R3, and so

Figure 13-1

Figure 13-2

Figure 13-3

Finally R", is in parallel with R4; hence the equivalent resistance of the entire circuit is

EMF and Internal Resistance

The work done per coulomb on the charge passing through a battery, generator, or other source of electric energy is called the electromotive force, or emf, of the source. The emf is equal to the potential difference across the terminals of the source when no current flows. When a current I flows, this potential difference is less than the emf because of the internal resistance of the source. If the internal resistance is r, then a potential drop of Ir occurs within the source. The terminal voltage V across a source of emf Ve whose internal resistance is r when it provides a current of I is therefore

V = Ve − Ir

Terminal voltage =emf − potential drop due to internal resistance

When a battery or generator of emf Ve is connected to an external resistance R, the total resistance in the circuit is R + r, and the current that flows is

Kirchhoff ’s Rules

The current that flows in each branch of a complex circuit can be found by applying Kirchhoff ’s rules to the circuit. The first rule applies to junctions of three or more wires (Figure 13-4) and is a consequence of conservation of charge. The second rule applies to loops, which are closed conducting paths in the circuit, and is a consequence of conservation of energy. The rules are:

1. The sum of the currents that flow into a junction is equal to the sum of the currents that flow out of the junction.

2. The sum of the emfs around a loop is equal to the sum of the IR

potential drops around the loop.

Figure 13-4

The procedure for applying Kirchhoff ’s rules is as follows:

1. Choose a direction for the current in each branch of the circuit, as in Figure 13-4. (A branch is a section of a circuit between two junctions.) If the choice is correct, the current will turn out to be positive. If not, the current will turn out to be negative, which means that the actual current is in the opposite direction. The current is the same in all the resistors and emf sources in a giv- en branch. Of course, the currents will usually be different in the different branches.

2. Apply the first rule to the currents at the various junctions. This gives as many equations as the number of junctions. However, one of these equations is always a combination of the others and so gives no new information. (If there are only two junction equations, they will be the same.) Thus, the number of usable junction equations is equal to one less than the number of junc- tions.

3. Apply the second rule to the emfs and IR drops in the loops. In going around a loop (which can be done either clockwise or counterclockwise), an emf is considered positive if the negative terminal of its source is met first. If the positive terminal is met first, the emf is considered negative. An IR drop is considered positive if the current in the resistor R is in the same direction as the path being followed. If the current direction is opposite to the path, the IR drop is considered negative.

In the case of the circuit shown in Figure 13-4, Kirchhoff ’s first rule, applied to either junction a or junction b, yields

I₁ = I₂ + I₃

The second rule applied to loop 1, shown in Figure 13-5(a), and pro- ceeding counterclockwise, yields

V_e,1 = I₁R₁ + I₂ R₂

The rule applied to loop 2, shown in Figure 13-5(b), and again proceed- ing counterclockwise, yields

−V_e,2 = − I₂ R₂ + I₃ R₃

There is also a third loop, namely, the outside one shown in Figure 13-5(c), which must similarly obey Kirchhoff ’s second rule. For the sake of variety, we now proceed clockwise and obtain

−V_e,1 + V_e,2 = − I₃ R₃ − I₁R₁

Figure 13-5

Labels: Electricity and Magnetism