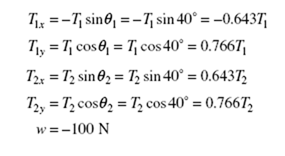
In This Chapter:
✔ Translational Equilibrium
✔ Rotational Equilibrium
✔ Center of Gravity
✔ Finding a Center of Gravity
Translational Equilibrium
A body is in translational equilibrium when no net force acts on it. Such a body is not accelerated, and it remains either at rest or in motion at constant velocity along a straight line, whichever its initial state was.
A body in translational equilibrium may have forces acting on it, but they must be such that their vector sum is zero. Thus the condition for the translational equilibrium of a body may be written
∑F = 0
where the symbol ∑ (Greek capital letter sigma) means “sum of ” and F refers to the various forces that act on the body.
The procedure for working out a problem that involves translational equilibrium has three steps:
1. Draw a diagram of the forces that act on the body. This is called a free-body diagram.
2. Choose a set of coordinate axes and resolve the various forces into their components along these axes.
3. Set the sum of the force components along each axis equal to zero so that
Sum of x force components = ∑Fx = 0
Sum of y force components = ∑Fy = 0
Sum of z force components = ∑Fz = 0
In this way, the vector equation ∑F = 0 is replaced by three scalar equations. Then solve the resulting equations for the unknown quantities.
A proper choice of directions for the axes often simplifies the calculations. When all the forces lie in a plane, for instance, the coordinate sys- tem can be chosen so that the x and y axes lie in the plane; then the two equations ∑Fx = 0 and ∑Fy = 0 are enough to express the condition for
translational equilibrium.
Solved Problem 8.1 A 100-N box is suspended from two ropes that each make an angle of 40° with the vertical. Find the tension in each rope.
Solution. The forces that act on the box are shown in the free-body dia- gram of Figure 8-1(a). They are
T1 = tension in left-hand rope
T2 = tension in right-hand rope
w = weight of box, which acts downward
Since the forces all lie in a plane, we need only x and y axes. In Figure 8-1(b), the forces are resolved into their x and y components, whose magnitudes are as follows:
Figure 8-1
Because T1x and w are, respectively, in the −x and −y directions, both have negative magnitudes.
Now we are ready for step 3. First we add the x components of the forces and set the sum equal to zero. This yields
Evidently, the tensions in the two ropes are equal. Next we do the same for the y components:
The tension in each rope is 65 N.
When the lines of action of the forces that act on a body in translational equilibrium intersect at a common point, they have no tendency to turn the body. Such forces are said to be concurrent. When the lines of action do not intersect, the forces are nonconcurrent and exert a net torque that acts to turn the body even though the resultant of the forces is zero (Fig- ure 8-2).
Figure 8-2
A body is in rotational equilibrium when no net torque acts on it. Such a body remains in its initial rotational state, either not spinning at all or spinning at a constant rate. The condition for the rotational equilibrium of a body may therefore be written
∑π= 0
where ∑π refers to the sum of the torques acting on the body about any point.
A torque that tends to cause a counterclockwise rotation when it is viewed from a given direction is considered positive; a torque that tends to cause a clockwise rotation is considered negative (Figure 8-3).
To investigate the rotational equilibrium of a body, any convenient point may be used as the pivot point for calculating torques; if the sum of the torques on a body in translational equilibrium is zero about some point, it is zero about any other point.
Center of Gravity
The center of gravity of a body is that point at which the body’s entire weight can be regarded as being concentrated. A body can be suspended in any orientation from its center of gravity without tending to rotate.
Solved Problem 8.2 (a) Under what circumstances is it necessary to consider torques in analyzing an equilibrium situation? (b) About what point should torques be calculated when this is necessary?
Solution. (a) Torques must be considered when the various forces that act on the body are nonconcurrent, that is, when their lines of action do not intersect at a common point. (b) Torques may be calculated about any point whatever for the purpose of determining the equilibrium of the body. Hence it makes sense to use a point that minimizes the labor involved, which usually is the point through which pass the maximum number of lines of action of the various forces; this is because a force whose line of action passes through a point exerts no torque about that point.
Finding a Center of Gravity
The center of gravity (CG) of an object of regular form and uniform composition is located at its geo- metric center. In the case of a complex object, the way to find its center of gravity is to consider it as a sys- tem of separate particles and then find the balance
point of the system. An example is the massless rod of Figure 8-4, which has three particles m1, m2, and m3 attached to it.
Figure 8-4
The CG of the system is at a distance X from the end of the rod such that the torque exerted by a single particle of mass M = m1 + m2 + m3 at X equals the sum of the torques exerted by the particles at their locations x1, x2, and x3. Thus,
This formula can be extended to any number of particles. If the complex object involves two or three dimensions rather than just one, the same procedure is applied along two or three coordinate axes to find X and Y or X, Y, and Z, which are the coordinates of the center of gravity.
Labels: Classical mechanics