
Ampere's law describes the magnetic field produced by a current-carrying wire. Two statements give a complete description of the magnetic field around a wire. The strength of the field is given by
where μo = 4π×10-7 Wb/A.m is the (magnetic) permeability. The direction of the field is (a vector) tangent to a circle about the current-carrying wire normal to the plane of the current. With the thumb of the right hand in the direction of the current the fingers naturally curl in the direction of the B fields tangent to concentric circles. The drawing on the left side of Fig. 35-1 is a view of a current coming out of the paper showing the field as a vector tangent to the circle and the drop off of the magnetic field with radius. The diagram on the right side is a three dimensional view of the magnetic field around a current-carrying wire.
Fig. 35-1
Ampere's law is written in the form of an integral
where i is the current contained within the path of the integral. This integral sign with a circle means that the integral is to be performed over a closed path. In this case the path is a circle in a plane normal to the current (see Fig. 35-1). The circular path is centered about the wire where the magnetic field is a constant. Over this circular path the magnetic field vector and dl, the vector representing an element of length of the circle are parallel so the sum of (integral of) their dot product, B. dl, is the constant B times the circumference of the circle or B(2πr). Remember that the dot product is the product of the projection of one vector onto another.
35-1 Calculate the magnetic field 7.0m below a power line carrying 12000A of current.
This is comparable to the earth's magnetic field. Assuming the power line is parallel to the surface of the earth then the magnetic field produced by this power line is also parallel to the surface of the earth.
<><><><><><><><><><><><>
35-2 Two long parallel wires separated by 0.60m carry antiparallel currents (the currents are physically parallel but in opposite directions) of 7.0 A each. What is the resulting field along the line between the wires and 0.40m from the lower wire?
Fig. 35-2
Solution: At the specified position the magnetic field due to wire 1 is
and directed as shown (right thumb in direction of current with fingers curled). The magnetic field due to wire 2 is 
The Force on Current Carrying Wires
Parallel wires carrying currents I1 and I2 produce a force on one other. Take the currents as parallel as shown in Fig. 35-3. The current in wire 1 produces a magnetic field at wire 2 of magnitude B1 = μoII/2πd. This field is directed down as shown and produces a force on wire 2 of magnitude F2=B1I2l. These forces are usually written in terms of force per unit length and this is most convenient in this problem. The force per unit length on wire 2 produced by the magnetic field associated with I1 is
Fig. 35-3
This is the experimental setup that is used to define the ampere. A current produces a magnetic field that produces a force on another current. Using Ampere's law and this setup current can be related directly to mechanical force.
<><><><><><><><><><><><>
35-3 Consider two wires coming out of the page carrying equal, and oppositely directed, currents as shown in Fig. 35-4. The wires are suspended from a common point with 0.40m long cords. The wires have a mass per unit length of 30 × 10-3 kg/m. Calculate the current to produce an angle of 6°.
Solution: This is a force-balance problem. The horizontal component of the tension (force) in the cord must equal the force due to the currents. Look at 1.0m of the wire. The mass of 1.0m of wire is 30 × 10-3 kg, and the force due to gravity mg = 0.29N. This must equal the vertical component of the tension in the cord. From the geometry,
Fig. 35-4
In Fig. 35-4 the separation of the wires is 2s where s is defined in the figure through sin6° = s/0.40m or s = 0.40m.sin6°. The electric force produced by the current in one wire producing a magnetic field that acts on the current in the other wire is
and this force must equal the mechanical force, or tension, in the cord so
<><><><><><><><><><><><>
35-4 Calculate the magnetic field 10cm perpendicular to the bisector of the line connecting two wires 2.0cm apart and carrying antiparallel currents of 100 A each as shown in Fig. 35-5.
Fig. 35-5
Solution: The magnitude of the magnetic field from each wire is μoI / 2πd. Because of the geometry the vertical components of B1 and B2 add to zero. The horizontal components add to a vector pointing toward the centerline
of the wires with magnitude B = 2B1sin θ. The dimension .
The magnitude of the resultant field is
Concentric Currents. In the statement of Ampere's law,
the i is the current contained within the path of the integral. This is illustrated in the following problem. Take a cylindrical conducting wire of radius 4a and total current I out of the plane of the page. The current is uniformly distributed over the cross-sectional area of the wire.
Fig. 35-6
First calculate the magnetic field at r = 6a using B = μoI/2πr: B = μoI/12πa.
Now calculate the magnetic field within the wire at a radius of 3a.
The I in this case is the fractional part of I contained within the 3a radius or
Another variation of this problem is concentric conductors with equal and opposite currents as shown in Fig. 35-7. Remember, the magnetic field over a circular path (Ampere's law) is related to the net current within the path.
The inner conductor is solid and has radius a. The outer conductor is hollow, having an inner radius b and an outer radius c. The currents are numerically equal but in opposite directions. Look at the magnetic field over several regions.
Fig. 35-7
Average Field Outside a Wire
Another application of Ampere's law involves the calculus concept of average value of a function.
35-5 Calculate the average value of the magnetic field from 0.50 to 0.10m radially out from a long wire carrying 100 A.
Solution: The magnetic field falls off radially according to B = μ 0I/2Πr. The average value of the function over this interval is the integral of the function (the area under the curve of B vs r) divided by the radial distance. See the Introduction, Mathematical Background, for the definition of the average value of a function.
Fig. 35-8
The Solenoid
A popular device that is based on the application of Ampere's law is the solenoid, a tightly wound coil producing a nearly uniform magnetic field along the axis of the coil. The coil is shown in Fig. 35-9.
Fig. 35-9
For tightly wound coils the windings take on the form of a sheet of current, and a cross section looks as shown in the middle drawing of the figure. The magnetic field around each coil of wire is such that the magnetic field is concentrated and nearly uniform inside the coil.
The integral around the path a → b → c → d → a is conveniently done in four parts. 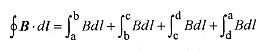
where N is the number of turns per length, so IoNL is the total current within the path.
35-6 Calculate the magnetic field inside a solenoid of 300 turns per centimeter carrying a current of 0.050A.
A toroid is a solenoid wrapped so as to form a circle. A section through a toroid is shown in Fig. 35-10.
Fig. 35-10
The application of Ampere's law is very straight forward. The path for the integral is along the center line of the toroid where the magnetic field is constant, so
where n is the total number of turns in the toroid. But n/2πr is the turns per unit length. Call this N, as before, so the field in a toroid is
35-7 Calculate the magnetic field in a toroid of 600 turns, current of 0.76A and center line radius 0.50m.
Labels: How To Solve Physics Problems