
Kirchhoff's laws applied to circuits containing multiple branches, voltage sources, and resistors allow calculation of currents in each branch of the circuit. Start with a very simple circuit consisting of a battery and resistor. The battery polarity is taken as indicated with positive charge
Fig. 31-1 leaving the positive plate. The current is as indicated by the arrow. An amount of charge or current over time starting at the negative plate of the battery is viewed as gaining energy in passing through the battery and losing this same amount of energy in the resistor. The equation for this circuit is shown in Fig. 31-1.
Kirchhoff Voltage Loop Equations.
The V - IR equation for this simple circuit illustrates the first Kirchhoff law: The algebraic sum of the changes in potential (energy) encountered in a complete traverse of a path is zero. This is analogous to a conservation of energy statement.
The only difficulty in applying Kirchhoff's laws is keeping the algebraic signs correct. When confused, go back to this simple diagram of a battery and resistor and the current flowing (in the external circuit) from the positive side of the battery through the resistor to the negative side of the battery. Write the V - IR = 0 statement establishing that when a battery is traversed in a positive direction, there is a gain in energy giving V a plus sign; and when a resistor is traversed in the direction of the current arrow, there is a loss in energy giving IR a negative sign. Every Kirchhoff law problem you do should have this little circuit drawn in a corner of the paper to remind you of the algebraic signs and their importance.
Think of a “piece of charge” traversing the circuit gaining energy as it passes through the battery and losing energy as it passes through the resistor. In this simple circuit the direction of the current is clear. In multiple branch circuits it is not possible to “guess” the correct directions for the currents. Make the best educated guess that you can and let the mathematics tell you whether the currents are positive or negative.
Fig. 31-2
Consider the three branch circuit of Fig. 31-2. Make your best estimate of the current direction for each resistor and draw and label the current arrows. It is not necessary to have the direction correct, it is only necessary to be consistent in applying the sign convention. Now make two loops around this circuit, one around the left and one around the right as indicated by the closed loops. Remember, when traversing a battery from minus to positive write +V and when traversing the resistor in the direction of the current arrow write -IR. Around the first loop
In traversing this loop start at the low, or negative, side of the 6V battery and proceed around the loop: 6 is positive
4I1 is negative because the resistor is traversed in the direction of the current arrow.
3I2 is positive because the resistor is traversed in the direction opposite to the current arrow.
7 is negative because the battery is traversed from plus to minus.
Writing the equations this way illustrates very clearly that they cannot be solved. In mathematical language they are two equations in three unknowns. The third equation necessary to solve for the three currents comes from the next Kirchhoff law.
Kirchhoff Current Junction Equations
The second Kirchhoff law deals with the currents: the sum of the currents to any junction must add to zero. This law is often forgotten. It is, however, easily remembered via a whimsical law called the “fat wire law.” The fat wire law is very simple. The sum of the currents to any junction must equal zero, otherwise the wire will get fat. Applying this second Kirchhoff law to the junction just above the 3Ω resistor
Now we have three independent equations in three unknowns.
NOTE: For convenience in the discussion, individual equations in a set of equations will be designated by letter symbols. The number of significant figures used in the calculations will be kept to a minimum so as not to obscure the mathematical procedure with numbers. Likewise, units will not be used. Several techniques for solving multiple equations in multiple unknowns will be presented. It is not necessary to know all these techniques. Pick a technique that you feel comfortable with and learn it well.
At this point you may be asking why we did not take another loop to obtain a third equation. Taking another loop in the circuit will only serve to generate another equation which is a linear combination of the first two loop equations. Take a loop around the outside of the circuit and write:
This equation is just the difference of the first two loop equations and is not a linearly independent third equation. Therefore it cannot be used to solve for the three currents. As an exercise take a figure eight path around the circuit and prove that this statement is also a linear combination of the first two loop equations.
Solving by Adding and Subtracting
Now to the solution of these three equations. The most popular and direct approach is to add and subtract equations to produce two equations in two unknowns and then further add and subtract to solve for one current and work backwards to find all the currents.
1 4I1+4I2+4I3=0
add (b) -4I1+3I2 =1
to obtain (α) 7I2- 4I3=1
Combine equation (α) with 2/3 of equation (c) and write (α) and (β)
Place I2 = 1/3 into (c).
3(1/3)+6I3=3 or I3 = 1/3
Now place I2 = 1/3 and I3 = 1/3 into (a). I1+(1/3)-(1/3)=0 or I1=0 Check these current values in each of the original equations to verify that they are correct.
Solving by Determinants
Another method of solving these equations is with determinants. Using determinants to solve three equations in three unknowns is explained in the Introduction, Mathematical Background. Your calculator may have an algorithm for solving simultaneous equations using determinants (sometimes called Cramer's rule), so this may be your method of choice.
Going back to the equations marked (a), (b), (c) set up the master determinant and expand along the first column. Equation (c) is divided by 3 to reduce the numbers.
The determinant for I1 is expanded along the top row
The determinant for I2 is expanded about the top row The value for
As an exercise set up the determinant for I3, expand along the top row, and verify the value of I3 obtained previously.
Solving by Augmented Matrix
A third method of solving three equations in three unknowns is with an augmented matrix. Many calculators that have internal programs for solving simultaneous equations require data to be input in a manner similar to the augmented matrix form. The manipulations of the augmented matrix are similar to adding and subtracting equations to find a solution. Before applying this method to the equations for this problem look at a general set of three equations in three unknowns.
If the first equation were multiplied by -(k/a) and added to the third equation these three equations would read
What this accomplishes is to make the coefficient of x zero in the third equation. Now multiply the first equation by -k/e and add to the second equation making the coefficient of x zero in the second equation. After this, the second equation can be multiplied by a constant and added to the third equation with the constant chosen so as to make the coefficient of y in the third equation zero. Once this is accomplished the solutions are easily written down. The procedure is better illustrated with a specific case, the previous problem. These equations already have some coefficients equal to zero making the process easier. This is usually the case with Kirchhoff law analysis
Multiply the first equation by 4 and add to the second equation generating a new second equation.
This makes the coefficient of I1 equal to zero in the second and third equation producing two equations in two unknowns. Now multiply the second equation by -1/7 and add to the third equation generating a new third equation.
Now solve directly with I3=1/3. Substituting this into the second equation I2=1/3. Putting these two values into the first equation obtains I1=0.
The augmented matrix method uses the coefficients from the equations. The adding and subtracting of equations to generate other equations is done by multiplying and adding different rows of the matrix just as if they were equations. As we go through the process imagine that the operations are being performed on equations. Working with the coefficients arranged in an orderly array is easier. Working the matrix so as to produce zeros starting in the lower left hand corner and then moving diagonally across the matrix is easier than working the equations. Start with
There is already a zero in the lower left corner so we need to create a zero in the -4 position. Multiply the first row by 4 and add to the second row generating a new second row. This is equivalent to multiplying the first equation by 4 and adding it to the second equation generating a new second equation, which is a linear combination of the first two. This is exactly what is done in solving simultaneous equations by adding and subtracting.
Now multiply the third row by -7 and add to the second row generating a new third row.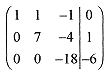
Now go back to the equations where 18I3 = 6 or I3=1/3.
Put I3=1/3 into 7I2-4I3=1 to obtain I2=1/3.
Put I2=1/3 and I3=1/3 to obtain I1=0.
These methods of solving multiple equations in multiple unknowns require considerable number manipulation with the attendant chance for error. The augmented matrix method has the least number manipulation while adding and subtracting may be more familiar to you. All of the techniques work. Pick the one that fits you, and the set of equations you are solving, best and proceed carefully.
Applications
The procedure for solving Kirchhoffs laws problems is the following:
1. Draw the battery and resistor circuit in the corner of your paper to remind you of the sign convention.
2. Place current arrows next to each resistor and label them.
3. Pick a junction and write the current statement.
4. Draw loops and write the loop equations.
5. Solve for the currents and check them in the original equations.
31-1 Solve for the current in each of the resistors in the circuit shown in Fig. 31-3.
Fig. 31-3
Solution: Follow the procedure for Kirchhoff problems. This is a subject that is conceptually easy but because of the large number of manipulations often hard to actually do. Work this problem as you are following along in the book.
Draw the circuit and begin. Draw the single battery and single resistor with current arrow and V - IR=0 equation.
Place and label the current arrows.
Write the statement of the “fat wire law” for the top center of the circuit. Write a loop statement for the left side of the circuit.
Write a loop statement for the right side of the circuit.
Now write these three equations in a convenient form for solution.
As an exercise solve these equations and verify that the solutions are I1 = 17/47 = 0.36, I2=24/47 = 0.51, and I3=7/47=0.15. Check these answers in the original equations.
31-2 Consider a more complicated problem as shown in Fig. 31-4 and calculate the currents in the resistors.
Fig. 31-4
Solution: Draw the battery and resistor circuit and V - IR equation to remind you of the algebraic sign convention.
Note the current arrows. Remember that if one of the currents comes out negative it means only that the current is opposite to the direction of your arrow.
Apply the “fat wire law” to the line across the top of the three resistors.
The loop around the top branch of the circuit is 6-8I1=0.
A loop around the lower left branch is 10-10I4-5I3-3=0.
A loop around the lower right branch is 3+5I3+6I2-6=0.
Rewrite the equations in convenient form for solving.
Immediately I1=3/4=0.75. Work the problem and verify that the other currents are I2=-0.20, I3=0.84, and I4=0.28.
31-3 Calculate the currents in the resistors of the circuit shown in Fig. 31-5.
Fig. 31-5
Solution: Draw the battery and resistor circuit and V - IR equation to remind you of the algebraic sign convention. Apply the “fat wire law” to the line across the top of the circuit. The loop around the left branch is 4 - 6I1 - 3I2 + 2 - 4I2 = 0.
The middle loop is 4I2 - 2 + 3I2 - 8I3 = 0.
The loop around the right branch is -3 + 5I4 + 8I3 = 0.
Rewriting the equations in convenient form for solving
Work the problem and verify that the currents are I1=0.41, I2=0.51, I3=0.19, and I4=0.29.
Hint: First solve for I3 using determinants, then the rest of the currents by algebra.
Labels: How To Solve Physics Problems