
The subject of mirrors and lenses is difficult to treat briefly first because for a thorough discussion there needs to be considerable attention to sign convention and second because different instructors and authors approach the subject with slight, but very significant differences that impact the working of problems.
The only way to become proficient in working with lenses and mirrors is to place the sign conventions appropriate to your course on a card in front of you and do problems drawing the rays and working the calculations. Be sure that you know the sign conventions and practice doing sample problems before taking any tests on mirrors or lenses. Signs will be your major (perhaps only) source of error. Sample sign conventions for mirrors and lenses are given below.
Sign Conventions for Mirrors
o is positive if object is in front of the mirror
o is negative if object is in back of the mirror
i is positive if the image is in front of the mirror
i is negative if the image is in back of the mirror
f is positive if the center of curvature is in front of the mirror
f is negative if the center of curvature is in back of the mirror
Sign Conventions for Lenses
o is positive if the object is in front of the lens
o is negative if the object is in back of the lens
i is positive if the image is in back of the lens
i is negative if the image is in front of the lens
f is positive for a converging lens
f is negative for a diverging lens
Mirrors.
An object placed in front of a plane mirror appears to an observer to be behind the mirror.
Fig. 45-1
Because of the law of reflection, divergent rays intercepted by the observer on reflection from the mirror appear to come from behind the mirror. The object distance, p, is numerically equal to the image distance, q. The image is called a virtual image because the light does not physically come from the image. A real image is one where the light comes from or passes through the image.
45-1 A light source is 4.0cm in front of a plane mirror. Where does an observer looking into the mirror see the image and is it real or virtual?
Solution: The image is 4.0cm behind the mirror. It is a virtual image because light does not pass through this image point.
A concave (converging) spherical mirror as shown in Fig. 45-2 can be analyzed by rays.
Fig 45-2
An object of height h placed at o, the object distance from the concave mirror, will produce a smaller image, h' at i, the image distance, according to the formula
where R is the radius of curvature and f(= R/2) is the focal length. The magnification is 
Draw a ray from the top of the object through the center of curvature (C in Fig. 45-2). Next draw a ray to the point where the principal axis (the horizontal line through C) intersects the mirror reflecting this ray back to intersect the one drawn previously. The intersection of these rays defines the top of the object. Drawing these rays requires experience. Set up several situations and draw the ray diagrams to become familiar with the procedure.
45-2 For a spherical concave mirror of 12cm radius of curvature describe the image of a 2.0cm height object placed 20cm on the center line of the mirror according to Fig. 45-2.
Solution: The image is inverted. The ray diagrams show this. Using the radius of curvature and the object distance find the image distance from
The height of the image is from
or h'=-0.86cm.
The image is 8.6cm from the mirror, inverted (minus sign) and real (rays pass through image).
<><><><><><><><><><><><>
When the object is at infinity (very far away) the mirror equation reduces to 1/i = 2/R, and we can say that the rays from infinity are focused at R/2. This defines the focal length as f = R/2.
A convex (diverging) spherical mirror is illustrated in Fig. 45-3.
Fig. 45-3
Objects placed in front of a convex mirror appear to come from behind the mirror, and they are smaller. First draw a ray from the top of the object parallel to the principal axis and reflect it from the mirror. This ray appears to come from the focus (behind the mirror). Next draw a ray so as to produce a reflected ray parallel to the principal axis of the mirror. The extension of this ray intersects the extension of the first one locating the top of the image.
The equations for concave mirrors also work for convex mirrors if a sign convention is adopted. Lengths where the light moves (to the left of the mirrors in Figs. 45-2 and 45-3) are positive, and lengths on the other side of the mirror (to the right of the mirror in Fig. 45-3) are negative. Lengths are measured (positive and negative) from the intersection of the principal axis and the mirror. These positive and negative regions are often referred to as the front and the back sides of the mirrors.
45-3 For a spherical convex mirror of 14cm radius of curvature, describe the image of a 2.5cm object placed 30cm out on the principal axis of the mirror.
Solution: Here is where we get into the signs. The focus and the image are on one side of the mirror and the object is on the other side. Therefore we take the focus as negative and expect the image distance to be negative. The image distance comes from equation 45-1 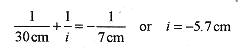
The height of the image is from
The minus sign for the image distance indicates that the image is behind the mirror, or on the same side as all the other minus signs. The plus sign for the magnification indicates that the image is erect (not inverted). The image is virtual.
Lenses
There are two types of thin lenses, converging and diverging, as shown in Fig. 45-4. 
The converging lens converges parallel rays to a point called the focus while a diverging lens refracts rays to make them appear as to come from a focus. The sign conventions become more involved for lenses than for mirrors. Rather than set out a sign convention, we will handle the signs in the context of each problem. The relationship between image distance, object distance and focal length is the same as for mirrors (equation 45-1).
45-4 A converging lens of focal length 8.0cm forms an image of an object placed 20cm in front of the lens. Describe the image.
Fig. 45-5
Solution: Draw a ray from the top of the object parallel to the axis then through the focus. Next draw a ray from the top of the object through the center of the lens to intersect the first ray. This locates the top of the object. Use equation 45-1 to find the image distance.
The magnification is (-) image distance over object distance or The image is located 13cm on the side of the lens opposite the object with magnification 0.67. It is inverted (minus sign) and real (rays pass through image).
45-5 A diverging lens has a 14cm focal length. Describe the image of a 4.0cm object placed 40cm from the lens.
Fig. 45-6
Solution: Draw a ray from the top of the object to the lens parallel to the principal axis and refract it back to the focus. Next draw a line from the top of the object through the center of the lens. The intersection of these rays locates the top of the object. The image distance is from equation 45-1.
The negative sign for the focal length is because this is a diverging lens. The image distance is negative because it is on the same side of the lens as the object (opposite to the converging lens). The magnification is 10/40 = 0.25.
The image is 0.25×4.0cm=1.0cm high, erect, virtual, and appears to come from a point 10cm from the lens on the same side as the object.
Go back over the problems in this chapter paying particular attention to the signs. As an exercise change the numbers in these problems and work them through until the sign conventions are clear in your mind. As you do more problems the logic of the sign convention listed on the first page of this chapter will become clear.
Labels: How To Solve Physics Problems