How To Solve Physics Problems Special Relativity problems and solutions

Special Relativity

 The special theory of relativity is based on two postulates.

1. The laws of physics are the same in all inertial reference frames. Inertial frames are reference (coordinate) frames moving at constant velocity with respect to one another; that is, they are not accelerating.

2. The speed of light is the same in all inertial frames. These two postulates lead to very interesting and highly significant conclusions concerning simultaneity and how we measure the fundamental quantities of length, mass, and time. These discussions, though very interesting, are inappropriate for a problems book, so we will go directly to the consequences of special relativity as it impacts our understanding of physics.

The concepts and calculations of special relativity require a change in how we view the world. Many of the things we study in special relativity may go against our intuition, but remember, intuition is often wrong and even if it were correct we have no experience to base our intuition on when dealing with particles approaching the speed of light where relativistic effects are observable. How many of Galileo's colleagues intuitively “knew” that when he dropped those two different sized balls from the Tower at Pisa the heavier one would reach the ground first? Success in understanding Special Relativity requires first that you rid your mind of intuitive knowledge based on what could be called “low velocity experience.” As you study Special Relativity you will encounter situations where you will be challenged to look at the postulates and change your view of the world.

Time Dilation.

Time intervals are different in different (moving) inertial frames. Place a light source, mirror, and detector in a moving vehicle as shown in Fig. 47-1. An observer in the moving vehicle measures the time for a light pulse to move from the source to the mirror and back to the detector as the distance traveled divided by the velocity of light, so Δt0 = 2d/c. The zero subscript indicates that this time is measured by an observer in the same frame where the event is taking place. This is also called the proper time.

 Fig 47-1

 An observer in another inertial frame observes the vehicle moving at a velocity v (see Fig. 47-2) and over the time interval of the event observes that the detector has traveled a distance vΔt.

Fig. 47-2

 The total distance the light has traveled is The time interval is Remember, c is the same to all observers regardless of inertial frame. The two times can be related with d = cΔto/2 so that The external observer of an event taking place in a moving reference frame, the one who measures Δt, always sees an event as taking longer than the stationary observer, the one who measures Δto, in the frame moving with the event.

 47-1 You are in a railroad car moving at constant velocity of zero with respect to the surface of the earth. What do you measure as the time it takes for a coin to drop 1.0m to the floor of the railroad car? What does an observer in another railroad car traveling at a constant 25m/s measure for this time?

Solution: You apply and observe The moving observer measures a time given by equation 47-1. For small v/c the best way to make this calculation is to use a binomial expansion of the radical (see, the Introduction, Mathematical Background). The first, and largest, relativistic correction term is This means that the correction is Δt = Δto(1+3.5 × 10-15)s. Time measurement this precise is beyond the capability of the cesium clocks. This is an unobservable effect.

<><><><><><><><><><><><>

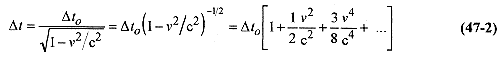
 47-2 For the situation of the previous problem take the moving observer from the train to a 2500m/s jet plane and then to a rocket ship traveling at 0.90c. (It is common, and very convenient in relativistic calculations, to express velocity as a fraction or decimal times c.)

Solution: Again using the binomial expansion and looking at the first term 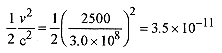This small a time difference is observable but it is a difficult experiment.

For the rocket ship traveling at 0.90c, use equation 47-1 directly.

The observer in the rocket ship measures the time for the falling coin as 1.0s, over twice what the stationary observer sees. These two problems illustrate how relativistic effects are observable only as relative velocities approach c.

 47-3 A “strange particle” is observed to move at 0.96c and have a lifetime of 2.0 × 10-8 s. What is the lifetime of the particle in its own reference frame?

 Solution: In equation 47-1 Δto is the (proper) time an observer traveling with the “strange particle” would measure so find

Length Contraction

The time dilation leads to a length contraction with velocity. Consider a vehicle moving at velocity v between two stars with one observer in the vehicle and another at a fixed (with respect to the stars) point. The external observer measures the (proper) distance between the stars as Lo, observes the velocity of the vehicle as v, and writes the time interval as Δt = Lo/v. The time interval Δt is not a proper time because measurement of Δt would required synchronized clocks at both stars. The observer in the vehicle sees the stars moving at t and measures a (proper) time interval Δto. This observer determines the distance between the stars as L = vΔto. Write these two equations as a fraction

and with

The length measured by a moving observer is contracted by a factor equal to

 47-4 In a soaring space ship (a vehicle capable of both space flight and conventional aircraft flight) you return from a space journey to find a new landing runway. Passing over this runway at 0.92c you measure its length as 1960m. What is its length at your landing speed of 200 m/s?

 Solution: At 200 m/s there is no observable relativistic effect. Use equation 47-3 to find the length of the runway at your landing speed.

47-5 How fast must a meter stick be traveling relative to your reference frame for you to observe a 2% contraction?

 Solution: Use equation 47-3 with L = 0.98Lo

Relativistic Momentum

At “low velocities” a force applied to a particle produces an acceleration according to the familiar F = d/dt (mv) = m(dv/dt). As the velocity of the particle approaches c, the momentum becomes velocity dependent with the force statement taking on the form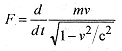 The most convenient interpretation is to associate the with the mass and say that the effective mass of a moving particle is where mo is the rest mass, measured with the mass not moving in the inertial frame where the measurements are made.

 47-6 What is the effective mass of an electron moving at 0.80c?

 Solution:

<><><><><><><><><><><><>

 47-7 Intergalactic space travelers need to know the relative velocities and masses of their space ships. Each ship, therefore, has a 1.0m long bar painted on the side of the ship alongside their rest mass. As you pass by a ship you measure this 1.0m bar as 0.93m. What is your relative velocity? You also observe their rest mass printed as 365,000kg. What is their mass relative to you? What does an observer in the other ship measure for your 1.0m bar?

 Solution: The length you observe is where Lo is the 1.0m, the length an observer at rest with respect to the vehicle would measure, and L is the length you measure so

The relativistic mass you observe is Observers in the other space ship measure your bar as 0.93m and relative speed as 0.37c.

<><><><><><><><><><><><>

As an exercise find the effective mass of an electron at 0.999c and at 0.99999c. As the velocity approaches c, the effective mass approaches infinity implying the necessity of an infinite force to reach c. This shows the theoretical impossibility of material objects traveling at c or beyond. 

Labels: How To Solve Physics Problems