Because we take another view of rotational motion in the beginning of this chapter, you may find it helpful to first review the discussion of rotational motion in the previous chapter.
Consider the rotation of a solid about some point in a plane. The rotation is counterclockwise in conformity with trigonometry. The angle is again defined as arc length over radius, the standard definition appropriate to radian measure θ= s / r.
Fig. 12 1
The average angular speed is defined as
with the instantaneous angular speed defined by
Similarly, the average angular acceleration is defined as
with the instantaneous acceleration defined as
The relationships between the point and the angle all start with s=rθ; then with successive derivatives comes
Remember that the radial, or center directed, acceleration is arad=v2/r = rw2.
A force has to be associated with the angular acceleration. Force, however, does not lend itself well to motion of a particle constrained to move in a circle, because most forces are not tangent to a circle. Torque works much better. Torque is defined in a rather unusual manner. Unusual, that is, until its utility is seen through experience in rotational dynamics.
Torque is the vector product of r, the vector from the axis of rotation to the rotating point, and F, the force applied at that point.
You may want to review the definitions of the cross product in the Introduction, Mathematical Background, before continuing. Most problems in torque can be done with the geometric interpretation of the cross product. Torque, r x F, is the product of r and the component of F perpendicular to r or \r\\F\ sin θ as shown on the left in Fig. 12 2.
Fig. 12 2
The torque vector is perpendicular to the plane of r and F and follows the right hand rule of rotating r into F. In this case the torque is out of the paper.
12 1 Calculate the torque on a 2.5kg mass constrained to rotate in a 1.6m radius circle with a 250N force applied at a (constant) angle of 35‹ between r and F.
Solution: The problem is depicted in Fig. 12 2. The definition of r x F. gives the direction of the torque as out of the paper. Application of the crossing of r into F is similar to generating a righthanded coordinate system by rotating x into y with the right hand with the thumb giving the direction of z. The magnitude of the torque is
Torque is r cross force, and similarly, angular momentum is r cross momentum or
Angular momentum is a vector in a direction perpendicular to the plane of r and p and magnitude equal to the product of r and the component of p perpendicular to r.
12 2 For the situation of problem 12 1 add that the linear velocity is 2.8m / s and find the angular momentum.
Solution: The linear momentum is mv = 2.5kg(2.8m/s)=7.0kg.m/s. The linear velocity is the tangential velocity, which is always at right angles to the radius; so the direction of the angular momentum vector is out of the paper, and the magnitude of the cross product is simplified because the sine of 90‹ is one.
<><><><><><><><><><><><>
With these definitions for torque and momentum, several relationships can be derived. Start with
Torque is the time derivative of angular momentum as force is the time derivative of linear momentum. Now, by analog, several things follow.
The total angular momentum of a system is the sum of the angular momentum of the individual pieces. Internal torques are equal and opposite, so only external torques change the angular momentum of the system. The statement
If the derivative of the total angular momentum is zero, the condition for no external torques, then the angular momentum is a constant.
Now look to the kinetic energy associated with rotating particles. Each particle, or piece, of a rotating mass has a linear speed v = rw, and the KE for each piece is a sum
This sum of the mr2's for the collection of pieces is called the rotational inertia, I, so that the KE can be written compactly as
The rotational inertia, I, is easy to calculate for individual particles and has been calculated for many shapes. Tabulations are found in most physics books and some mathematical tables.
12 3 Calculate the rotational inertia for one 2.0kg mass at the end of a 3.0m rod of negligible mass and then the rotational inertia of a dumbbell consisting of two 2.0kg masses on the ends of a 6.0m long rod of negligible mass pivoted about the center of the rod.
Solution: For the one mass, the sum of the mr2's is just 2.0kg(9.0m2)=18kg.m2.
For the dumbbell, there are two masses, and the rotational inertia would be 36kg.m2.
Notice that if the dumbbell were rotated about one mass then the rotational inertia would be 2.0kg(36m2 = 72kg.m2. This is of course neglecting the extent of the mass close around the rotating axis.
<><><><><><><><><><><><>
The total momentum of a rotating mass (point) is mvr. If the mass is rotating, then v is perpendicular to r leading to a simple statement of angular momentum.
Angular momentum is L = mvr = mr2 w = IW.
By definition
The power is
Angular momentum, as a property of the motion, is conserved and is a powerful tool in solving certain problems in rotational motion. First, calculate a torque using the vector form for position and force and the determinant for the cross product. See the Introduction, Mathematical Background for a review of this definition of cross products.
Most problems do not require as extensive a calculation as this equation would indicate. For a position and force vector in the x y plane the torque reduces to a single z component.
12 4 Calculate the angular momentum of a 3.0kg mass at 3.0m in the x direction and 2.0m in the y direction and with velocity components of 20m/s in the x direction and
30m / s in the y direction?
Fig. 12 3
Solution: Write r and p in vector form: r=(3.0i 2.0j)m p=(60i 90j)kg.m/s The angular momentum is
The angular momentum vector is 150kg.m2 / s pointed into the paper.
Second Solution: Now redo the problem with angle and magnitude. The angle between r and p is 22.6‹. Figure 12 3 shows the trigonometric relations. Note that the angle between r and p is negative. The fact that the angle is negative can be easily missed. Rather than rely on the sign of the angle, the better way to determine the direction of the angular momentum vector is to use the right hand rule and cross r into p with the thumb giving the direction of L. The magnitude of L is
Now to a few problems with rotating hoops and cylinders using rotational dynamics, conservation of energy, and conservation of angular momentum.
12 5 A hoop of mass 1.0kg and radius 0.25m is rotating in a horizontal plane with angular momentum 4.0kg.m2 / s. A lump of clay of mass 0.20kg is placed (gently) on the hoop. What happens to the angular velocity of the hoop?
Solution: The moment of inertia for a hoop (from the table in your text) is I = mr2.
The angular momentum, L, is Iw,, so the initial angular velocity can be calculated from L = Iwi
Since the lump of clay is placed (gently) on the hoop (The hoop is rotating in the horizontal plane, and the clay is placed on the hoop vertically.), placing the clay only adds mass to the hoop. This additional mass adds
(another) moment of inertia mr2, so with the angular momentum the same (no external torque has acted to change it)
<><><><><><><><><><><><>
12 6 An amusement park game consists of a paddle wheel arrangement where you shoot at the paddles with a pellet gun, thereby turning the wheel. The paddle wheel is set in motion with an initial angular momentum of 200kg.m2 / s and angular frequency of 4.0rad / s. You shoot eight 40g pellets at a speed of 200m/s at the paddles. The pellets hit the paddles at 0.80m radius, stick, and impart all their momentum to the wheel. Find the new angular momentum and the new angular frequency.
Solution: First calculate the initial moment of inertia of the paddle wheel from L = Iw.
Fig. 12 4
Now calculate the w after the wheel has absorbed the (momentum in the) eight pellets. The angular momentum of each pellet is the linear momentum times the 0.80m radius.
For eight pellets the (absorbed) angular momentum is Lall pellets = 51.2 kg.m2/ 2
The new angular momentum is the original plus this, or 251.2 kg.m2 / s.
The I also has increased because of the additional mass at the 0.80m radius. This (additional)/ is
The equation for calculating the new angular velocity
<><><><><><><><><><><><>
12 7 Now consider a 10kg solid cylindrical drum with radius 1.0m rotating about its cylindrical axis under the influence of a force produced by a 30kg mass attached to a cord wound around the drum. What is the torque, moment of inertia, and angular acceleration?
Fig 12 5
Solution: The moment of inertia for a solid drum rotating about its axis is mr2 / 2.
The torque on the drum is the tension in the cable times the radius of the drum. This tension is much like the tension encountered in the problems of multiple blocks sliding on tables as found in Chapter 5, Force. The system accelerates clockwise, so the unbalanced force on M makes it accelerate according to
The torque on the drum makes it angularly accelerate according to rF =lα
The acceleration of M is the same as the tangential acceleration, a=rĄ so
12 8 When the 30kg mass in problem 12 7 has fallen (starting from rest) through 4.0m, what is the linear velocity, angular velocity of the drum, and the time for this to occur?
Solution: This part of the problem is approached from an energy point of view. The 30kg mass falls through a distance of 4.0m. The work performed by gravity Goesinto translational
KE of the 30kg mass and rotational KE of the cylinder. The main difficulty in problems like this is remembering that some of the work performed results in rotational KE and some in translational KE.
Putting in the numbers
Fromv = rω angular velocity is
The time for this system to reach this velocity is from ω=ωo+τ1. <><><><><><><><><><><><>
12 9 A solid sphere is constrained to rotate about a vertical axis passing through the center of the sphere. A cord is wrapped around what would be the equator, passes over a pulley of negligible mass, and is attached to a mass that is allowed to fall under the influence of gravity. Write a conservation of energy statement for the system.
Fig. 12 6
Solution: If the mass falls a distance h, then the energy gained by the system is Mgh. This energy Goesinto translational kinetic energy of the mass and rotational kinetic energy of the sphere. A conservation of energy statement is
The velocity of a point on the string and the velocity of the mass are the same and are related to the angular velocity through v = rω, so the energy statement can be written in terms ofv. Additionally, the formula for I=2mr2/5 can be substituted so
Note that the energy statement could have been written in terms of ω rather than v.
12 10 For problem 12 9 take the mass of the sphere as m=2.0kg,r=0.30m, the hanging mass as M= 0.80 kg, and the height the mass falls through as h=1.5m. Find the velocity of the hanging mass, and the angular momentum of the sphere.
Solution: The velocity of the mass, the rope, and a point on the equator of the sphere (all the same velocity) is
from the energy statement
The angular velocity of the sphere is
The angular momentum of the sphere is
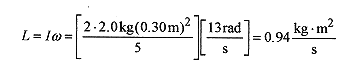
As an added exercise give the pulley in this problem a mass and a radius and go through the problem again. Remember that I and ω will be different for the pulley.
Labels: How To Solve Physics Problems