
The wave nature of light is used to explain the several diffraction and interference phenomena discussed in this chapter.
Double Slit Diffraction
Figure 46-1 shows the setup for the classic Young's double slit experiment first performed around 1800.
Fig. 46-1
Monochromatic light passes through a sufficiently narrow slit to produce a coherent source for the double slits. The coherent (in phase) light spreads out from each of the slits creating an interference pattern on the screen. The geometry for the interference is shown in Fig. 46-1. Destructive interference occurs when the path length differs by one-half wavelength and constructive interference occurs when the path length is an integral number of wavelengths. From the figure we can write the criteria for constructive interference as The distance from the central maxima (opposite the center of the two slits) to the first bright fringe on the screen is related to the angle via tan θ = ym/R. For small angles, which is the case with the Young's experiment, sinθ ≈ tanθ = θ, so equation 46-1 can be rewritten as
Historically this experiment was used to measure the wavelength of light.
46-1 A Young's experiment is set up with slit separation 2.0 × 10-4 m, screen distance 0.80m, and distance from central maxima to second bright fringe 3.9 × 10-3 m. What is the wavelength of the source?
<><><><><><><><><><><><>
46-2 In a different Young's experiment with 488nm light the second dark fringe is 1.2 × 10-3 m away from the center of the central bright fringe. The screen is 1.2m from the slits. What is the separation of the slits?
Solution: This second dark fringe corresponds to 3/2 of a wavelength in path difference. One wavelength path difference is 2/3 of the 1.2 × 10-3 m or 8.0 × 10-4 m. This number now fits with equation 46-2 (one wavelength path difference), and solving for d
Single Slit Diffraction
The intensity distribution pattern for single slit diffraction is similar to the pattern for double slit diffraction. The geometry and analysis, however, are quite different. Coherent light incident on a narrow slit (100 to 1000 wavelengths wide) produces a fringe pattern as shown in Fig. 46-2.
Fig. 46-2
In the analysis of single slit, or Fraunhofer, diffraction we will use the dark fringes. The slit of width a is viewed as a region where interference occurs between light at the top of the slit and the middle of the slit. The particular situation for the first dark fringe obtains for corresponding pairs of source points separated by a/2 across the width of the slit. The criterion for dark fringes is
Again sinθ is approximately the same as tanθ, which is approximately the same as θ. So rewrite equation 46-3 with this approximation as
where m corresponds to the number of the dark fringes away from the central maxima.
46-3 Monochromatic light is incident on a 4.0 × 10-4 m wide slit producing a Fraunhofer diffraction pattern on a screen 1.5m away. The distance from the central maxima to the second dark fringe is 3.4 × 10-3 m. What is the wavelength of the light?
Solution: Reworking equation 46-4 yields
<><><><><><><><><><><><>
46-4 Light from a He-Ne laser of 633nm is incident on a 2.0 × 10-4 m wide slit. What is the width of the central maxima (the distance between the dark fringes on either side of the central maxima) on a screen 2.0m away.
Solution: Rearranging equation 46-4, the distance to the first dark fringe is The width of the central maxima is two times this value or 1.3 × 10-2 m.
The Diffraction Grating
A diffraction grating consists of multiple slits as shown in Fig. 46-3. When light is incident on this arrangement constructive interference occurs when the path difference between adjacent slits is mλ. Increasing the number of slits produces two effects: the intensity of each interference maximum increases, and the width of each interference maximum decreases. This makes the grating a very convenient tool for the study of the various component wavelengths (spectra) of gases.
Fig. 46-3
46-5 A grating with 2000 lines per cm is illuminated with a hydrogen gas discharge tube. Two of the hydrogen lines are at 410 and 434 nm. What is the first order spacing of these lines on a screen 1.0 m from the grating. The experimental arrangement is shown in Fig. 46-4.
Fig. 46-4
Solution: The phrase “first order” refers to the first maxima.
First find the spacing 1.0 × 10-2 m/2000 lines = 5.0 × 10-6 m.
For the 410 nm line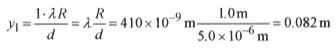
The lines are separated by 5 mm on the screen.
Labels: How To Solve Physics Problems