How To Solve Physics Problems Oscillating L-C Circuits problems and solutions

Oscillating L-C Circuits

 In the next two chapters we will look at L-C and R-L-C circuits from two different points of view. Our view in this chapter is concerned with the transient response of the circuit, that is how the circuit responds to an initially charged capacitor. In the next chapter we will look at how the circuit behaves when it is driven by a sinusoidal voltage source.

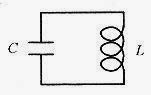
 L-C Circuits Charge a capacitor and place it in series with an inductor as shown in Fig. 40-1.

Fig.40-1

When the charged capacitor is connected to the inductor, the maximum possible voltage is applied across the inductor. This maximum voltage results in the maximum rate of increase in current in the circuit, vL = L(di/dt). As time goes on, the voltage drops, the rate of change in current drops, but the current increases. Maximum current and zero voltage across the capacitor are coincident. The current continues in the same direction until the capacitor is fully charged in the opposite (from original) direction. In the absence of energy-consuming resistance the voltage (across the capacitor) and current (in the circuit) continue to vary sinusoidally 90° out of phase.

This circuit behaves analogous to the mechanical mass-spring system with the capacitor playing the role of the spring and the inductor playing the role of the mass. Voltage is analogous to the compression of the spring. Energy stored in the spring is equal to kx2/2, and energy stored in the capacitor is equal to CV2/2. Current is analogous to the velocity of the mass. Energy stored in the velocity of the mass is equal to mv2/2, and energy stored in the inductor is equal to Li2/2. Zero spring displacement is coincident with maximum velocity of the mass, as zero voltage is coincident with maximum current.

The Kirchhoff loop statement for this circuit is This equation can be rewritten with q the only time dependent variable as This equation has the same form as the one for the simple harmonic oscillator. (See Chapter 15, Simple Harmonic Motion.) It is solved by asking the question, “What function differentiated twice produces a negative constant times itself?” A sine or cosine function is the obvious answer, so “guess” q = qo cosωt with and putting this into the Kirchhoff equation , we see immediately that the frequency is The circuit oscillates between maximum electric field in the capacitor and zero current in the circuit, and maximum current in the circuit and zero charge (and field) in the capacitor.

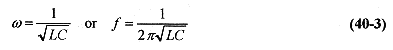
 40-1 An L-C circuit consists of a 50mH inductor and a 40 μF capacitor. What is the frequency of oscillation of this circuit? If the maximum charge on the capacitor is 100 μC, what is the maximum voltage on the components?

 Solution: The frequency The maximum voltage on either component is the same as the maximum voltage on the capacitor, which comes from the basic definition of capacitance In an ideal circuit with no resistance, there is no way for energy to enter or leave the system, and the total energy must be passed back and forth between capacitor and inductor. Energy is stored in the electric field of the capacitor and the magnetic field of the inductor. The maximum energy in each component is equal, so

40-2 For the circuit described in problem 40-1, what is the maximum energy and the maximum current in the circuit?

Solution: Maximum energy is

The maximum current is from ,so

 R-L-C Circuits

The introduction of series resistance produces the circuit of Fig. 40-2.

Fig. 40-2

If the capacitor is initially charged (before it is placed in the circuit), oscillation will occur. The total energy in the circuit, however, will not remain constant but decrease at the rate of i2R, the power dissipated in the resistor as heat.

A Kirchhoff-type voltage equation for the circuit can be written Again, rewriting with q The introduction of the iR term makes the equation much more difficult to solve. It is, however, identical in form to the equation for the damped harmonic oscillator found in Chapter 15, Simple Harmonic Motion. The addition of the iR term produces an exponential envelope to the oscillations. The specific solution is where This exponential envelope of a sinusoidal oscillation is what we would expect from this circuit; oscillations that decrease exponentially. While this equation hasn't been derived, it can be justified by taking the appropriate derivatives and substituting back into equation 40-6.

 40-3 An R-L-C circuit consists of a 10Ω resistor, 200mH inductor, and a 10μF capacitor. The capacitor is initially charged to 10μC. What is the maximum possible voltage on the capacitor (as dictated by the exponential envelope) at 0.10s?

Solution: The voltage on the capacitor is proportional to the charge. The value of the exponential function at any time is determined by taking the cosine function as 1. Using equation 40-6 the charge is

The notation for e has been switched to exp for convenience.

The voltage at this time is

Labels: How To Solve Physics Problems