Motion: Velocity , Acceleration , Distance, Velocity, and Acceleration , Acceleration of Gravity , Falling Bodies and Projectile Motion

Motion

In This Chapter:
✔ Velocity
✔ Acceleration
✔ Distance, Velocity, and Acceleration
✔ Acceleration of Gravity
✔ Falling Bodies
✔ Projectile Motion
Velocity
The velocity of a body is a vector quantity that describes both how fast it is moving and the direction in which it is headed.
In the case of a body traveling in a straight line, its velocity is simply the rate at which it covers distance. The average velocity ¯v of such a body when it covers the distance s in the time t is
The average velocity of a body during the time t does not completely describe its motion, however, because during the time t, it may sometimes have gone faster than ¯v and sometimes slower. The velocity of a body at any given moment is called its instantaneous velocity and is given by
Here, Ds is the distance the body has gone in the very short time interval Dt at the specified moment. (D is the capital Greek letter delta.) Instanta- neous velocity is what a car’s speedometer indicates.
When the instantaneous velocity of a body does not change, it is moving at constant velocity. For the case of constant velocity, the basic formula is
Solved Problem 2.1 The velocity of sound in air at sea level is about 343 m/s. If a person hears a clap of thunder 3.00 s after seeing a lightning flash, how far away was the lightning?
Solution. The velocity of light is so great compared with the velocity of sound that the time needed for the light of the flash to reach the person can be neglected. Hence

Acceleration

A body whose velocity is changing is accelerated. A body is accelerated when its velocity is increasing, de- creasing, or changing its direction.
The acceleration of a body is the rate at which its velocity is changing. If a body moving in a straight line has a velocity of v0 at the start of a certain time interval
t and of v at the end, its acceleration is

A positive acceleration means an increase in velocity; a negative acceleration (sometimes called deceleration) means a decrease in velocity. Only constant accelerations are considered here.
The defining formula for acceleration can be rewritten to give the final velocity v of an accelerated body:
We can also solve for the time t in terms of v0, v, and a:

Velocity has the dimensions of distance/time. Acceleration has the dimensions of velocity/time or distance/time2. A typical acceleration unit is the meter/second2 (meter per second squared). Sometimes two different time units are convenient; for instance, the acceleration of a car that goes from rest to 90 km/h in 10 s might be expressed as a = 9 (km/h)/s.
Solved Problem 2.2 A car starts from rest and reaches a final velocity of 40 m/s in 10 s. (a) What is its acceleration? (b) If its acceleration remains the same, what will its velocity be 5 s later?
Solution. (a) Here v₀ = 0. Hence

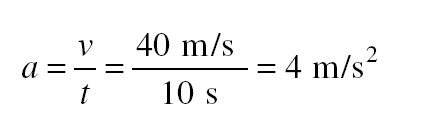
(b) Now v0 = 40 m/s, soDistance, Velocity, and Acceleration
Let us consider a body whose velocity is v0 when it starts to be accelerated at a constant rate. After time t, the final velocity of the body will be
How far does the body go during the time interval t? The average velocity v¯ of the body is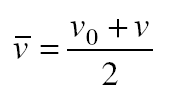


and so
Since v = v0 + at, another way to specify the distance covered during t is
If the body is accelerated from rest, v0 = 0 and
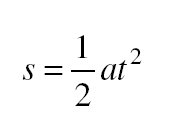
Another useful formula gives the final velocity of a body in terms of its initial velocity, its acceleration, and the distance it has traveled during the acceleration:
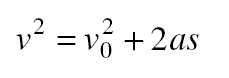
This can be solved for the distance s to give
In the case of a body that starts from rest, v_o = 0 and
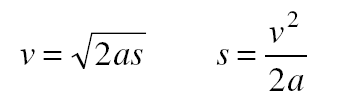
Table 2.1 summarizes the formulas for motion under constant acceleration.
Acceleration of Gravity
All bodies in free fall near the earth’s surface have the same downward acceleration of
A body falling from rest in a vacuum thus has a velocity of 32 ft/s at the end of the first second, 64 ft/s at the end of the next second, and so forth. The farther the body falls, the faster it moves.
You Need to Know

A body in free fall has the same downward acceleration whether it starts from rest or has an initial velocity in some direction.

The presence of air affects the motion of falling bodies partly through buoyancy and partly through air resistance. Thus two different objects falling in air from the same height will not, in general, reach the ground at exactly the same time. Because air resistance
increases with velocity, eventually a falling body reaches a terminal velocity that depends on its mass, size, and shape, and it cannot fall any faster than that.
Falling Bodies
When buoyancy and air resistance can be neglected, a falling body has the constant acceleration g and the formulas for uniformly accelerated motion apply. Thus a body dropped from rest has the velocity
after time t, and it has fallen through a vertical distance ofFrom the latter formula, we see that
and so the velocity of the body is related to the distance it has fallen by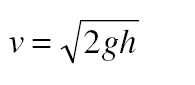To reach a certain height h, a body thrown upward must have the same initial velocity as the final velocity of a body falling from that height, namely, v = 2gh .
Solved Problem 2.3 What velocity must a ball have when thrown up- ward if it is to reach a height of 15 m?
Solution. The upward velocity the ball must have is the same as the downward velocity the ball would have if dropped from that height. Henc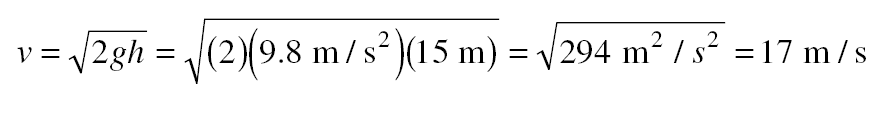Projectile Motion
The formulas for straight-line motion can be used to analyze the hori- zontal and vertical aspects of a projectile’s flight separately because these are independent of each other. If air resistance is neglected, the horizon- tal velocity component vx remains constant during the flight. The effect of gravity on the vertical component vy is to provide a downward accel- eration. If vy is initially upward, vy first decreases to 0 and then increases in the downward direction.
The range of a projectile launched at an angle q above the horizon- tal with initial velocity v0 isThe time of flight iIf θ₁is an angle other than 45° that corresponds to a range R, then a second angle θ₂ for the same range is given by
as shown in Figure 2−1.
Solved Problem 2.4 A football is thrown with a velocity of 10 m/s at an angle of 30° above the horizontal. (a) How far away should its intended receiver be? (b) What will the time of flight be?
Solution.