Power and Refrigeration Gas Cycles: The Brayton Cycle , The Regenerative Brayton Cycle and The Gas Refrigeration Cycle
7.5 The Brayton Cycle
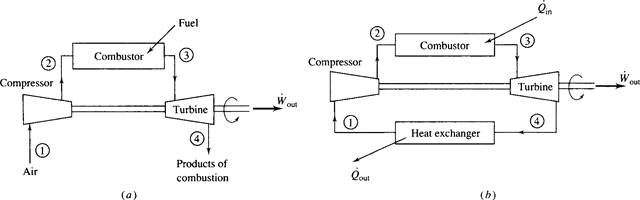
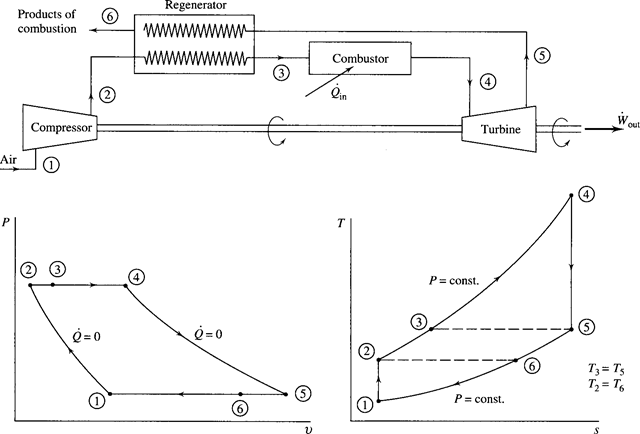
The gas turbine is another mechanical system that produces power. It may operate on an open cycle when used as a truck engine, or on a closed cycle when used in a power plant. In open cycle operation, air enters the compressor, passes through a constant-pressure
combustion chamber, then through a turbine, and finally exits as products of combustion to the atmosphere, as shown in Fig. 7.4a. In closed cycle operation the combustion chamber is replaced with a heat exchanger in which energy enters the cycle from some exterior source; an additional heat exchanger transfers heat from the cycle so that the air is returned to its initial state, as shown in Fig. 7.4b.
The ideal cycle used to model the gas turbine is the Brayton cycle. It utilizes isentropic compression and expansion, as indicated in Fig. 7.5. The efficiency of such a cycle is given by
Figure 7.4 The Brayton cycle components. (a) Open cycle. (b) Closed cycle.
Figure 7.5 The Brayton cycle.
Using the isentropic relations
This expression for thermal efficiency was obtained using constant specific heats. For more accurate calculations the gas tables from App. E should be used.
In an actual gas turbine the compressor and the turbine are not isentropic; some losses do occur. These losses, usually in the neighborhood of 15 percent, significantly reduce the efficiency of the gas-turbine engine.
Another important feature of the gas turbine that seriously limits thermal efficiency is the high work requirement of the compressor, measured by the back work ratio,
BWR = W&comp / W&turb. The compressor may require up to 80 percent of the turbine’s
output (a back work ratio of 0.8), leaving only 20 percent for net work output. This
relatively high limit is experienced when the efficiencies of the compressor and tur- bine are too low. Solved problems illustrate this point.
EXAMPLE 7.5
Air enters the compressor of a gas turbine at 100 kPa and 25°C. For a pressure ratio of 5 and a maximum temperature of 850°C, determine the back work ratio (BWR) and the thermal efficiency for this Brayton cycle. Assume constant specific heat.
Solution
To find the back work ratio we observe that
EXAMPLE 7.6
Assume the compressor and the gas turbine in Example 7.5 each have an efficiency of 75 percent. Determine the back work ratio (BWR) and the thermal efficiency for the Brayton cycle, assuming constant specific heats.
Solution
We can calculate the desired quantities if we determine wcomp, wturb, and qin. The compressor work is
where ws,comp is the isentropic work and T2′ is the temperature of state 2′ assuming n isentropic process where state 2 is the actual state. We then have, using T= T2 rom Example 7.5,
Likewise, there results
It is obvious why the Brayton cycle cannot operate efficiently with relatively low efficiencies of the compressor and turbine. Efficiencies had to be raised into the 90’s before the Brayton cycle became a cycle that could effectively be used to produce power.
7.6 The Regenerative Brayton Cycle
The heat transfer from the simple gas-turbine cycle of the previous section is simply lost to the surroundings—either directly, with the products of combustion—or from a heat exchanger. Some of this exit energy can be utilized since the temperature of the flow exiting the turbine is greater than the temperature of the flow entering the compressor. A counterflow heat exchanger, a regenerator, is used to transfer some of this energy to the air leaving the compressor, as shown in Fig. 7.6. For an ideal regenerator the exit temperature Twould equal the entering temperature T ; and, similarly, Twould equal T . Since less energy is rejected from the cycle, the thermal efficiency is expected to increase. It is given by
Using the first law, expressions for q and wturb are found to be
Figure 7.6 The regenerative Brayton cycle. Hence, for the ideal regenerator in which T
= T5 and q = wturb , the thermal efficiency can be written as
Using the appropriate isentropic relation, after some algebra, this can be written in the form
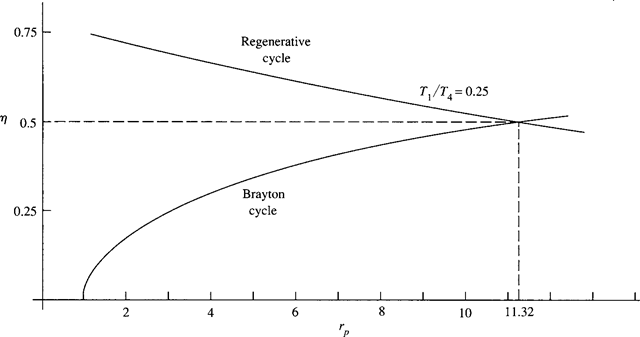
Note that this expression for thermal efficiency is quite different from that for the Brayton cycle. For a given pressure ratio, the efficiency increases as the ratio of minimum to maximum temperature decreases. But, perhaps more surprisingly, as the pressure ratio increases the efficiency decreases, an effect opposite to that of the Brayton cycle. Hence it is not surprising that for a given regenerative cycle temperature ratio, there is a particular pressure ratio for which the efficiency of the Brayton cycle will equal the efficiency of the regenerative cycle. This is shown for a temperature ratio of 0.25 in Fig. 7.7.
Figure 7.7 Efficiencies of the Brayton and regenerative cycles.
In practice the temperature of the air leaving the regenerator at state 3 must be less than the temperature of the air entering at state 5. Also, T > T . The effective- ness, or efficiency, of a regenerator is measured by
if we assume an ideal gas with constant specific heats. For the ideal regenerator T3 = T5
and hreg = 1. Regenerator efficiencies exceeding 80 percent are common.
EXAMPLE 7.7
Add an ideal regenerator to the gas-turbine cycle of Example 7.5 and calculate the thermal efficiency and the back work ratio, assuming constant specific heats.
Solution
The thermal efficiency is found using Eq. (7.24):
This represents a 57 percent increase in efficiency, a rather large effect. Note that, for the information given, the back work ratio does not change; hence,
BWR = wcomp/wturb = 0.420.
7.7 The Combined Cycle
The Brayton cycle efficiency is quite low primarily because a substantial amount of the energy input is exhausted to the surroundings. This exhausted energy is usually at a relatively high temperature and thus it can be used effectively to produce power. One possible application is the combined Brayton Rankine cycle in which the high- temperature exhaust gases exiting the gas turbine are used to supply energy to the boiler of the Rankine cycle, as illustrated in Fig. 7.8. Note that the temperature T9 of the Brayton cycle gases exiting the boiler is less than the temperature T of the
Figure 7.8 The combined Brayton-Rankine cycle.
Rankine cycle steam exiting the boiler; this is possible in the counterflow heat exchanger, the boiler.
To relate the air mass flow rate m& a of the Brayton cycle to the steam mass flow rate m& s of the Rankine cycle, we use an energy balance in the boiler; it gives (see Fig. 7.8),
assuming no additional energy addition in the boiler, which would be possible with an oil burner, for example. The cycle efficiency would be found by considering the
purchased energy as Q&in , the energy input in the combustor. The output is the sum
of the net output W> from the gas turbine and the output W&ST from the steam turbine. The combined cycle efficiency is thus given by
An example will illustrate the increase in efficiency of such a combined cycle.
EXAMPLE 7.8
A simple steam power plant operates between pressures of 10 kPa and 4 MPa with a maximum temperature of 400°C. The power output from the steam tur- bine is 100 MW. A gas turbine provides the energy to the boiler; it accepts air at 100 kPa and 25°C, and has a pressure ratio of 5 and a maximum temperature of 850°C. The exhaust gases exit the boiler at 350 K. Determine the thermal efficiency of the combined Brayton-Rankine cycle. Refer to Fig. 7.8.
Solution
If we neglect the work of the pump, the enthalpy remains unchanged across the pump. Hence, h2 = h1 = 192 kJ/kg. At 400°C and 4 MPa we have h3 = 3214 kJ/kg and s3 = 6.769 kJ/kg · K. State 4 is located by noting that s4 = s3 so that the quality is
Note that this efficiency is 59 percent higher than the Rankine cycle (see Example 6.2) and 53 percent higher than the Brayton cycle (see Example 7.5). Using steam reheaters, steam regenerators, gas intercoolers, and gas reheaters could increase cycle efficiency even more.
7.8 The Gas Refrigeration Cycle
If the flow of the gas is reversed in the Brayton cycle of Fig. 7.5, the gas undergoes an isentropic expansion process as it flows through the turbine, resulting in a substantial reduction in temperature, as shown in Fig. 7.9. The gas with low turbine exit temperature can be used to refrigerate a space to temperature T by extracting heat at rate Q&in from the refrigerated space.
Figure 7.9 illustrates a closed refrigeration cycle. (An open cycle system is
used in aircraft; air is extracted from the atmosphere at state 2 and inserted into the passenger compartment at state 1. This provides both fresh air and cooling.) An additional heat exchanger may be used, like the regenerator of the Brayton power cycle, to provide an even lower turbine exit temperature, as illustrated in Example 7.10. The gas does not enter the expansion process (the turbine) at state 5; rather, it passes through an internal heat exchanger (it does not exchange heat with the surroundings). This allows the temperature of the gas entering the
Figure 7.9 The gas refrigeration cycle.
turbine to be much lower than that of Fig. 7.9. The temperature T after the expansion is so low that gas liquefaction is possible. It should be noted, how- ever, that the coefficient of performance is actually reduced by the inclusion of an internal heat exchanger.
A reminder: when the purpose of a thermodynamic cycle is to cool or heat a space, we do not define a cycle’s efficiency; rather, we define its coefficient of performance:
EXAMPLE 7.9
Air enters the compressor of a simple gas refrigeration cycle at −10°C and
100 kPa. For a compression ratio of 10 and a turbine inlet temperature of 30°C,
calculate the minimum cycle temperature and the coefficient of performance using the ideal-gas equations of this section.
Solution
Assuming isentropic compression and expansion processes we find
The COP is now calculated as follows:
This coefficient of performance is quite low when compared with that of a vapor refrigeration cycle. Thus, gas refrigeration cycles are used only for special applications.
EXAMPLE 7.10
Use the given information for the compressor of the refrigeration cycle of Example 7.9 but add an ideal internal heat exchanger, a regenerator, as illustrated
below, so that the air temperature entering the turbine is −40°C. Calculate the
minimum cycle temperature and the coefficient of performance.
Solution
Assuming isentropic compression we again have
Quiz No. 1
(Assume constant specific heats)
1. Which of the following statements is not true of the diesel cycle?
(A) The expansion process is an isentropic process.
(B) The combustion process is a constant-volume process.
(C) The exhaust process is a constant-volume process.
(D) The compression process is an adiabatic process.
2. An engine with a bore and a stroke of 0.2 m × 0.2 m has a clearance of
5 percent. Determine the compression ratio.
(A) 23
(B) 21
(C) 19
(D) 17
3. A Carnot piston engine operates with air between 20 and 600°C with a low pressure of 100 kPa. If it is to deliver 800 kJ/kg of work, calculate MEP. (See Figs. 5.5 and 5.6.)
(A) 484 kPa
(B) 374 kPa
(C) 299 kPa
(D) 243 kPa
4. The heat rejected in the Otto cycle of Fig. 7.2 is
(A) Cp (T4 − T1 )
(B) Cp (T3 − T4 )
(C) Cv (T4 − T1 )
(D) Cv (T3 − T4 )
5. The maximum allowable pressure in an Otto cycle is 8 MPa. Conditions at the beginning of the air compression are 85 kPa and 22°C. Calculate the required heat addition if the compression ratio is 8.
(A) 2000 kJ/kg
(B) 2400 kJ/kg
(C) 2800 kJ/kg
(D) 3200 kJ/kg
6. The MEP for the Otto cycle of Prob. 5 is nearest
(A) 900 kPa
(B) 1100 kPa
(C) 1300 kPa
(D) 1500 kPa
7. A diesel cycle operates on air which enters the compression process at 85 kPa and 30°C. If the compression ratio is 16 and the maximum temperature is 2000°C, the cutoff ratio is nearest
(A) 2.47
(B) 2.29
(C) 2.04
(D) 1.98
8. If the power output of the diesel cycle of Prob. 7 is 500 hp, the mass flow rate of air is nearest
(A) 0.532 kg/s
(B) 0.467 kg/s
(C) 0.431 kg/s
(D) 0.386 kg/s
9. Air enters the compressor of a gas turbine at 85 kPa and 0°C. If the pressure ratio is 6 and the maximum temperature is 1000°C, using the ideal-gas equations, the thermal efficiency is nearest
(A) 52%
(B) 48%
(C) 44%
(D) 40%
10. Using the ideal-gas law, the back work ratio for the Brayton cycle of Prob.
9 is nearest
| (A) | 0.305 |
| (B) | 0.329 |
| (C) | 0.358 |
| (D) | 0.394 |
11. For the ideal-gas turbine with regenerator shown below, W& out is nearest
(A) 950 kW
(B) 900 kW
(C) 850 kW
(D) 800 kW
12. The back work ratio for the cycle of Prob. 11 is nearest
| (A) | 0.432 |
| (B) | 0.418 |
| (C) | 0.393 |
| (D) | 0.341 |
13. Air enters the compressor of an ideal-gas refrigeration cycle at 10°C and 80 kPa. If the maximum and minimum temperatures are 250 and −50°C,
the compressor work is nearest
(A) 170 kJ/kg
(B) 190 kJ/kg
(C) 220 kJ/kg
(D) 240 kJ/kg
14. The pressure ratio across the compressor in the cycle of Prob. 13 is nearest
(A) 7.6
(B) 8.2
(C) 8.6
(D) 8.9
15. The COP for the refrigeration cycle of Prob. 13 is nearest (A) 1.04
(B) 1.18
(C) 1.22
(D) 1.49
Quiz No. 2
(Assume constant specific heats)
1. The exhaust process in the Otto and diesel cycles is replaced with a constant-volume process for what primary reason?
(A) To simulate the zero work of the actual exhaust process.
(B) To simulate the zero heat transfer of the actual process.
(C) To restore the air to its original state.
(D) To ensure that the first law is satisfied.
2. An air-standard cycle operates in a piston-cylinder arrangement with the following four processes: 1 → 2: isentropic compression from 100 kPa and 15°C to 2 MPa; 2 → 3: constant-pressure heat addition to 1200°C; 3 → 4: isentropic expansion; and 4 → 1: constant-volume heat rejection. Calculate
the heat addition.
(A) 433 kJ/kg
(B) 487 kJ/kg
(C) 506 kJ/kg
(D) 522 kJ/kg
3. A Carnot piston engine operates on air between high and low pressures of 3 MPa and 100 kPa with a low temperature of 20°C. For a compression ratio of 15, calculate the thermal efficiency. (See Figs. 5.5 and 5.6.)
(A) 40%
(B) 50%
(C) 60%
(D) 70%
4. A spark-ignition engine operates on an Otto cycle with a compression ratio of 9 and temperature limits of 30 and 1000°C. If the power output is 500 kW, the thermal efficiency is nearest
(A) 50%
(B) 54%
(C) 58%
(D) 64%
5. The mass flow rate of air required for the Otto cycle of Prob. 4 is nearest
(A) 1.6 kg/s
(B) 1.8 kg/s
(C) 2.2 kg/s
(D) 2.0 kg/s
6. A diesel engine is designed to operate with a compression ratio of 16 and air entering the compression stroke at 110 kPa and 20°C. If the energy added during combustion is 1800 kJ/kg, calculate the cutoff ratio.
(A) 3.2
(B) 3.0
(C) 2.8
(D) 2.6
7. The MEP of the diesel cycle of Prob. 6 is nearest
(A) 1430 kPa
(B) 1290 kPa
(C) 1120 kPa
(D) 1080 kPa
8. Air enters the compressor of a Brayton cycle at 80 kPa and 30°C and compresses it to 500 kPa. If 1800 kJ/kg of energy is added in the combustor, calculate the compressor work requirement.
(A) 304 kJ/kg
(B) 286 kJ/kg
(C) 232 kJ/kg
(D) 208 kJ/kg
9. The new output of the turbine of Prob. 8 is nearest
(A) 874 kJ/kg
(B) 826 kJ/kg
(C) 776 kJ/kg
(D) 734 kJ/kg
10. The BWR of the Brayton cycle of Prob. 8 is nearest (A) 0.22
(B) 0.24
(C) 0.26
(D) 0.28
11. A regenerator is installed in the gas turbine of Prob. 8. Determine the cycle efficiency if its effectiveness is 100 percent.
(A) 88%
(B) 85%
(C) 82%
(D) 79%
12. The engines on a commercial jet aircraft operate on which of the basic cycles?
(A) Otto
(B) Diesel
(C) Carnot
(D) Brayton
13. Air flows at the rate of 2.0 kg/s through the compressor of an ideal-gas refrigeration cycle where the pressure increases to 500 kPa from 100 kPa.
The maximum and minimum cycle temperatures are 300 and −20°C,
respectively. Calculate the power needed to drive the compressor fluid
using the ideal-gas equations.
(A) 198 kW
(B) 145 kW
(C) 126 kW
(D) 108 kW
14. The COP of the refrigeration cycle of Prob. 13 is nearest (A) 2.73
(B) 2.43
(C) 1.96
(D) 1.73
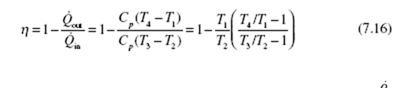



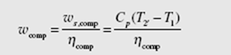


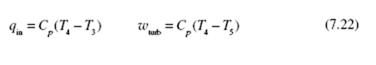



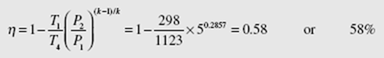
![image_thumb[1] image_thumb[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEixlnx_qsRkdkaLeZHSWwmMXVexkMxY8ADS-LAKWyHcSqnscBakQUtklDM_rbhGOWywaSKrcZIx1LyUbGllNOs-YvkJfa68G0qwBMKxsI-m_Tw2hRYfHXH9cveY3nFZJUGhMmdu8DhNsfz9/?imgmax=800)
![image_thumb[3] image_thumb[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgP57OL1koNrAF6CdXJfHPThn_J-_F806uMIvDFdhbgjpzLrcbesVeqVNBuov6Ze7g3Y65N-bMS4hBtkPqvZ4FIMqod87EvI3gi2E8_z2pwbtm-293GcPoQtQYo2XSatY5cE974tV4pKHFq/?imgmax=800)
![image_thumb[4] image_thumb[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhflEpswy-4PtAiwIO9RWESNKTxqP8fQjOgqIYjMIRqlmo0la6eu2-OulpFBzH7V3TOZnWeYZDoBj_aMKwzX_sBxLtt22s2DUxvF5W5378d2cw9FYzI14zKL2SGRO-oDs7fa4YY7xvSBLHz/?imgmax=800)
![image_thumb[5] image_thumb[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh8NIvv6eqG43cncQvCQSdvF5ajUItwAh25fec1EbySyAshg8Ooum4JSWBfLb_YbFACM_YQus9Kyyps6qn8gp6OccyDWJNl2ZVLySDReMrA6q2yaI44ubQnAVJYC3_qK9446tMFauPdhmJs/?imgmax=800)
![image_thumb[6] image_thumb[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgJDg3Ds-UN5WS6p268r33I_7EEzNoRnLi_4IdacLaCJ3tu7jAsxVUn3MOn4xqkYMYiOINnxpKx_0C778AnCAHFaRy3t40HuySGsDfb70u86L4KjVT7EF6U0Y83K1Vs5dnSu5uErsP2aq6M/?imgmax=800)
![image_thumb[8] image_thumb[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi0uNJ-Pd37jqmIBdwmc9ZclvLhn3pxEInBxaZfaT4HZTvyUngyZJ4JuRNDiXrhOV3B_SHGOlW3Q6GSW8ihSOmCUHjMxTOIcYlca5vlPZkMbYl7FDltLFjRdCpeVKRx3C8IDAeeimM-FTs9/?imgmax=800)
![image_thumb[9] image_thumb[9]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiDuZF0zUHg9OJNsi1r9qKy1-A7Im6oipJdlBKc0cF4FfOnjrqPUd443mkLF2DTlHp08qKipfikjeHbYs4aYEGtay2gC2pfdRuFeFpfq-6lXq2-QyoC26feTlm89frH-Oui2C-VfuMG-ERG/?imgmax=800)
![image_thumb[10] image_thumb[10]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgR68nH3N6Yi654IxFqC5THTgEXl-zEq7OZpVpqlPukXnFvn3n-pP-VnFkYR_PeFiBkHS5HTsshqUzYEQeSosYJeH9VANtjYhTFZHP-3Snlqnfu2S66tlWl8xNnLWTFnaHSyDXsi_ZcOGqe/?imgmax=800)
![image_thumb[11] image_thumb[11]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjk8cQDQ94zHTYr4Hwm1qXs8Njs9c1sp5caaO2LeR-fELKP-Ixj8XrDofpg8UW9DJz8BaxTXqP-AxoGf9GFyXsX6C6xJoCt__K5k4rcYpYQbbxtOjnW7J-RZXn0Cv19qyktjOt7W6ITMw1-/?imgmax=800)
![image_thumb[12] image_thumb[12]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgj3x7hNXxgYKw2aiUDiepWiKEA5pzCCXIcE9bCLbWzr7leJaNTg0Tnh_SlVd72vE6ba1qUxE9wzplHALkNojdPd2zYl77ccKINdg_8xjy4NOqgrdarMVBFr_OQLSNW8DzBjpsGOtz2ZLi1/?imgmax=800)
![image_thumb[13] image_thumb[13]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiUGYQwf-9EUTEhzxnWFy2Bg3Lh5gfevNKwDzqOS9a5B0q7j3ng0kudJGi1ffcNjHvTsE49gLTETt0hgo0EBSxcICia0gBGyQtizUMnEXaFKInRB8S9t-ZX2F0RJ6R26JIR-HMNqHYs00mw/?imgmax=800)


