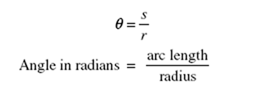
In This Chapter:
✔ Angular Measure
✔ Angular Velocity
✔ Angular Acceleration
✔ Moment of Inertia
✔ Torque
✔ Rotational Energy and Work
✔ Angular Momentum
Angular Measure
In everyday life, angles are measured in degrees, where 360º equals a full turn. A more suitable unit for technical purposes is the radian (rad). If a circle is drawn whose center is at the vertex of a particular angle (Fig-ure 7-1), the angle q (Greek letter theta) in radians is equal to the ratio between the arc s cut by the angle and the radius r of the circle:
Figure 7-1
Because the circumference of a circle of radius r is 2pr, there are 2p rad in a complete revolution (rev). Hence
1 rev = 360° = 2π rad
and so,
1° = 0.01745 rad 1 rad = 57.30°
The angular velocity of a body describes how fast it is turning about an axis. If a body turns through the angle q in the time t, its angular veloci- ty w (Greek letter omega) is
Angular velocity is usually expressed in radians per second (rad/s), revolutions per second (rev/s or rps), and revolutions per minute (rev/min or rpm), where
1 rev/s = 2π rad/s = 6.28 rad/s
1 rev/min =(2π /60) rad/s = 0.105 rad/s
The linear velocity v of a particle that moves in a circle of radius r with the uniform angular velocity w is given by
v = ωr
Linear velocity = (angular velocity)(radius of circle)
This formula is valid only when w is expressed in radian measure.
A rotating body whose angular velocity changes from ω0 to ωf in the time interval t has the angular acceleration a (Greek letter alpha) of
A positive value of a means that the angular velocity is increasing; a negative value means that it is decreasing. Only constant angular accelerations are considered here.
The formulas relating the angular displacement, velocity, and acceleration of a rotating body under constant angular acceleration are analogous to the formulas relating linear displacement, velocity, and acceleration. If a body has the initial angular velocity w0, its angular velocity ωf
after a time t during which its angular acceleration is a will be
ωf = ωo + at
and, in this time, it will have turned through an angular displacement of
θ= ωot + (1/2)at 2
A relationship that does not involve the time t directly is sometimes useful:
ωf2 = ωo2 + 2aθ
Solved Problem 7.1 A phonograph turntable initially rotating at 3.5 rad/s makes three complete turns before coming to a stop. (a) What is its angular acceleration? (b) How much time does it take to come to a stop?
Solution.
(a) The angle in radians that corresponds to 3 rev is
Moment of Inertia
The rotational analog of mass is a quantity called moment of inertia. The greater the moment of inertia of a body, the greater its resistance to a change in its angular velocity.
Let us imagine a rigid body divided into a great many small particles whose masses are m1, m2, m3, … and whose distances from the axis of rotation are respectively r1, r2, r3, … (Figure 7-2).
The moment of inertia of this body is given by
I = m1r1 2+ m2r2 2+ m3r3 2+ L = Σmr2
where the symbol S (Greek capital letter sigma) means “sum of ” as be- fore. The farther a particle is from the axis of rotation, the more it con- tributes to the moment of inertia. The units of I are kg · m2 and slug · ft2. Some examples of moments of inertia of bodies of mass M are shown in Figure 7-3.
Torque
The torque t (Greek letter tau) exerted by a force on a body is a measure of its effectiveness in turning the body about a certain pivot point. The moment arm of a force F about a pivot point O is the perpendicular distance L between the line of action of the force and
O (Figure 7-4). The torque τ exerted by the force about O has the magnitude
Figure 7-4 Four directions along which a force F can be applied to a wrench. In (a) the moment arm L is longest, hence the torque t = FL is a maximum. In (d ) the line of action of F passes through the pivot O, so L = 0 and t = 0.
The torque exerted by a force is also known as the moment of the force. A force whose line of action passes through O produces no torque about O because its moment arm is zero.
Torque plays the same role in rotational motion that force plays in linear motion. A net force F acting on a body of mass m causes it to un- dergo the linear acceleration a in accordance with Newton’s second law of motion F = ma. Similarly, a net torque t acting on a body of moment of inertia I causes it to undergo the angular acceleration a (in rad/s2) in accordance with the formula
t = Ia
Torque= (moment of inertia) (angular acceleration)
Rotational Energy and Work
The kinetic energy of a body of moment of inertia I whose angular ve- locity is w (in rad/s) is
KE =( 1/2 )Iω2
Kinetic energy =( 1/2 )(moment of inertia) (angular velocity)2
The work done by a constant torque τ that acts on a body while it experiences the angular displacement θ rad is
W = πω
Work= (torque) (angular displacement)
The rate at which work is being done when a torque τ acts on a body that rotates at the constant angular velocity w (rad/s) is
P = πω
Power= (torque) (angular velocity)
Angular Momentum
The equivalent of linear momentum in rotational motion is angular momentum. The angular momentum L of a rotating body has the magnitude
L = Iω
Angular momentum = (moment of inertia) (angular velocity)
The greater the angular momentum of a spinning object, such as a top, the greater its tendency to spin.
Like linear momentum, angular momentum is a vector quantity with direction as well as magnitude. The direction of the angular momentum of a rotating body is given by the right-hand rule (Figure 7-5):
Figure 7-5
When the fingers of the right hand are curled in the direction of rotation, the thumb points in the direction of L.
According to the principle of conservation of angular momentum, the total angular momentum of a system of bodies remains constant in the absence of a net torque regardless of what happens within the system. Be- cause angular momentum is a vector quantity, its conservation implies that the direction of the axis of rotation tends to remain unchanged.
Table 7.1 compares linear and angular quantities.
Labels: Classical mechanics