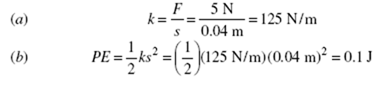
In This Chapter:
✔ Restoring Force
✔ Elastic Potential Energy
✔ Simple Harmonic Motion
✔ Period and Frequency
✔ Displacement, Velocity, and Acceleration
✔ Pendulums
Restoring Force
When an elastic object such as a spring is stretched or compressed, a restoring force appears that tries to re- turn the object to its normal length. It is this restoring force that must be overcome by the applied force in order to deform the object. From Hooke’s law, the restoring force Fr is proportional to the displacement s provided the elastic limit is not exceeded. Hence
Restoring force= − (force constant) (displacement)
The minus sign is required because the restoring force acts in the opposite direction to the displacement. The greater the value of the force con- stant k, the greater the restoring force for a given displacement and the greater the applied force F = ks needed to produce the displacement.
Because work must be done by an applied force to stretch or compress an object, the object has elastic potential energy, where
PE = 1/2 ks2
When a deformed elastic object is released, its elastic potential energy turns into kinetic energy or into work done on something else.
Solved Problem 9.1 A force of 5 N compresses a spring by 4 cm. (a) Find the force constant of the spring. (b) Find the elastic potential energy of the compressed spring.
Solution.
Simple Harmonic Motion
In periodic motion, a body repeats a certain motion indefinitely, always returning to its starting point after a constant time interval and then starting a new cycle. Simple harmonic motion is periodic motion that occurs when the restoring force on a body displaced from an equilibrium position is proportional to the displacement and in the opposite direction. A mass m attached to a spring executes simple harmonic motion when the spring is pulled out and released. The spring’s PE becomes KE as the
mass begins to move, and the KE of the mass becomes PE again as its momentum causes the spring to overshoot the equilibrium position and become compressed (Figure 9-1).
The amplitude A of a body undergoing simple harmonic motion is the maximum value of its displacement on either side of the equilibrium position.
The period T of a body undergoing simple harmonic motion is the time needed for one complete cycle; T is independent of the amplitude A. If the acceleration of the body is a when its displacement is s,
In the case of a body of mass m attached to a spring of force constant k, Fr = −ks = ma, and so −s/a = m/k. Hence
The frequency f of a body undergoing simple harmonic motion is the number of cycles per second it executes, so that
The unit of frequency is the hertz (Hz), where 1 Hz = 1 cycle/s.
If t = 0 when a body undergoing simple harmonic motion is in its equilibrium position of s = 0 and is moving in the direction of increasing s, then at any time t thereafter its displacement is
s = A sin 2pft Often, this formula is written
where w = 2pf is the angular frequency of the motion in radians per second. Figure 9-2 is a graph of s versus t.
The velocity of the body at time t is
When v is positive, the body is moving in the direction of increasing s; when v is negative, it is moving in the direction of decreasing s. In terms of the displacement s, the magnitude of the velocity is
The acceleration of the body at time t is
In terms of the displacement s, the acceleration is
a = 4p2f 2s
A simple pendulum has its entire mass concentrated at the end of the string, as in Figure 9-3(a), and it undergoes simple harmonic motion pro-
Figure 9-3
vided that the arc through which it travels is only a few degrees. The period of a simple pendulum of length L is
The physical pendulum of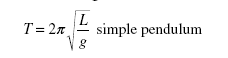 
A torsion pendulum consists of an object suspended by a wire or thin rod, as in Figure 9-3(c), which undergoes rotational simple harmonic oscillations. From Hooke’s law, the torque t needed to twist the object through an angle q is
provided the elastic limit is not exceeded, where K is a constant that de- pends on the material and dimensions of the wire. If I is the moment of inertia of the object about its point of suspension, the period of the oscillation is
Solved Problem 9.2 A lamp is suspended from a high ceiling with a cord 12 ft long. Find its period of oscillation.
Solution.
Labels: Classical mechanics
![Simple Harmonic Motion]_Page_070_Image_0001](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjmboSeT9vdgGZPlhj6JH0HpBF1JgpCAO4l6BFkNG4l-LB0YvM7q9ZMHFDY7b-x0hbWBf-ASEilh2LJMYmxLx-1gkbylT0cZlw4TCFZ6HUAmg4AOYAalYNIPVXcJsuWvu20jQKgQKzfLpJQ/s1600-h/Simple%252520Harmonic%252520Motion%25255D_Page_070_Image_0001%25255B2%25255D.jpg "Simple Harmonic Motion]_Page_070_Image_0001")
![Simple Harmonic Motion]_Page_070_Image_0002](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEisQ9Y7sPeV23rRswUCgiKtNpJUCldLoJe76HpGSSSlZsO6mqFNLio8B2IguhRQWHBbJ5seq3Zg54PtL8VEb_EC15uI2oMBzG0Zt8H2xUnbaDdxTIQDxKuO9AL0SHzKL0oGX6Kzu5k2MeAc/s1600-h/Simple%252520Harmonic%252520Motion%25255D_Page_070_Image_0002%25255B2%25255D.jpg "Simple Harmonic Motion]_Page_070_Image_0002")
