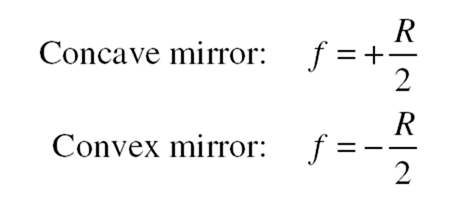
In This Chapter:
✔ Focal Length
✔ Ray Tracing
✔ Mirror Equation
✔ Magnification
Focal Length
Figure 18-1 shows how a concave mirror converges a parallel beam of light to a real focal point F, and Figure 18-2 shows how a convex mirror diverges a parallel beam of light so that the reflected rays appear to come from a virtual focal point F behind the mirror. In either case, if the radius of curvature of the mirror is R, the focal length f is R/2. For a concave mirror, f is positive, and for a convex mirror, f is negative. Thus
The axis of a mirror of either kind is the straight line that passes through
C and F.
Figure 18-1
Figure 18-2
Ray Tracing
The position and size of the image formed by a spherical mirror of an ob- ject in front of it can be found by constructing a scale drawing by tracing two different light rays from each point of interest in the object to where they (or their extensions, in the case of a virtual image) intersect after be- ing reflected by the mirror. Three rays especially useful for this purpose are shown in Figure 18-3; any two are sufficient:
Figure 18-3
1. A ray that leaves the object parallel to the axis of the mirror. Af- ter reflection, this ray passes through the focal point of a con- cave mirror or seems to come from the focal point of a convex mirror.
2. A ray that passes through the focal point of a concave mirror or is directed toward the focal point of a convex mirror. After re- flection, this ray travels parallel to the axis of the mirror.
3. A ray that leaves the object along a radius of the mirror. After reflection, this ray returns along the same radius.
When an object is a distance p from a mirror of focal length f, the image is located a distance q from the mirror, where
This equation holds for both concave and convex mirrors (see Figure 18-4). The mirror equation is readily solved for p, q, or f :
A positive value of p or q denotes a real object or image, and a negative value denotes a virtual object or image. A real object is in front of a mirror; a virtual object appears to be located behind the mirror and must itself be an image produced by another mirror or lens. A real image is formed by light rays that actually pass through the image, so a real image will appear on the screen placed at the position of the image. But a virtual image can be seen only by the eye since the light rays that appear to come from the image actually do not pass through it.
Remember
Figure 18.4
The linear magnification m of any optical system is the ratio between the size (height or width or other transverse linear dimensions) of the image and the size of the object. In the case of a mirror,
A positive magnification signifies an erect image, as in Figure 18-4(b); a negative one signifies an inverted image, as in Figure 18-4(a). Table 18.1 is a summary of the sign conventions used in connection with spherical mirrors.
Table 18.1
Labels: Optics