Work transferred by a rotating shaft (Fig. 3.6) is a common occurrence in mechanical systems. The work results from the shearing forces due to the shearing stress τ, which varies linearly with the radius over the cross-sectional area. The differential shearing force due to the shearing stress is
dF = τ dA = τ (2π rdr) (3.6)
The linear velocity with which this force moves is rω. Hence, the rate of doing work (force times velocity) is
where R is the radius of the shaft. The torque T is found from the shearing stresses by integrating over the area:
Figure 3.6 Work due to a rotating shaft transmitting a torque.
Combining this with Eq. (3.7) above, we have
W· = Tω (3.9)
To find the work transferred in a given time Δt, we simply multiply Eq. (3.9) by the number of seconds:
W = TωΔt (3.10)
The angular velocity must be expressed in rad/s. If it is expressed in rev/min (rpm), we must multiply by 2π /60.
The work necessary to stretch a linear spring (Fig. 3.7) with spring constant K from a length x1 to x2 can be found by using the relation for the force:
F = Kx (3.11)
where x is the distance the spring is stretched from the unstretched position. Note that the force is dependent on the variable x. Hence, we must integrate the force over the distance the spring is stretched; this results in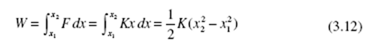
W = Vi Δt (3.13)
The power would be the rate of doing work, or
W = Vi (3.14)
Figure 3.7 Work needed to stretch a spring.
Figure 3.8 Work due to a current flowing through a resistor.
EXAMPLE 3.5
The drive shaft in an automobile delivers 100 N · m of torque as it rotates at 3000 rpm. Calculate the horsepower transmitted.
Solution .
The power is found by using W = Tw. This requires w to be expressed in rad/s:
EXAMPLE 3.6
The air in a 10-cm-diameter cylinder shown is heated until the spring is com- pressed 50 mm. Find the work done by the air on the frictionless piston. The spring is initially unstretched, as shown.
Solution
The pressure in the cylinder is initially found from a force balance as shown on the free-body diagram:
To raise the piston a distance of 50 mm, without the spring, the pressure would be constant and the work required would be force times distance:
W = PA × d = 162 500 × (π × 0.052 ) × 0.05 = 63.81 J
Using Eq. (3.12), the work required to compress the spring is calculated to be
The total work is then found by summing the above two values:
Wtotal = 63.81 + 12.5 = 76.31 J
In the preceding sections we considered several work modes. Transfer of energy that we cannot account for by any of the work modes is called heat transfer. We can define heat transfer as energy transferred across the boundary of a system due to a difference in temperature between the system and the surroundings of the system. A process in which there is zero heat transfer is called an adiabatic process. Such a process is approximated experimentally by sufficiently insulating the system so that the heat transfer is negligible. An insulated system in thermodynamics will always be assumed to have zero heat transfer.
Consider a system composed of a hot block and a cold block of equal mass. The hot block contains more energy than the cold block due to its higher temperature. When the blocks are brought into contact with each other, energy flows from the hot block to the cold one by means of heat transfer until the blocks attain thermal equilibrium, with both blocks arriving at the same temperature. Once in thermal equilibrium, there are no longer any temperature differences, therefore, there is no longer any heat transfer. Energy in the hot block has simply been transferred to the cold block, so that if the system is insulated, the cold block gains the amount of energy lost by the hot block.
It should be noted that the energy contained in a system might be transferred to the surroundings either by work done by the system or by heat transferred from the system. In either case, heat and work are qualitatively equivalent and are expressed in units of energy. An equivalent reduction in energy is accomplished if 100 J of heat is transferred from a system or if 100 J of work is performed by a system. In Fig. 3.9 the burner illustrates heat being added to the system and the rotating shaft
Figure 3.9 Energy added to a system.
illustrates work being done on the system. In either case, energy is being added to the system.
Although heat and work are similar in that they both represent energy crossing a boundary, they differ in that, unlike work, convention prescribes that heat transferred to a system is considered positive. Thus, positive heat transfer adds energy to a system, whereas positive work subtracts energy from a system.
Because a system does not contain heat, heat is not a property. Thus, its differential is inexact and is written as d Q, where Q is the heat transfer. For a particular process between state 1 and state 2 the heat transfer could be written as Q 1-2 but it will generally be denoted simply as Q. It is sometimes convenient to refer to the heat transfer per unit mass, or q, defined as
Often we are interested in the rate of heat transfer, or in the heat flux, denoted by Q& with units of J/s = W.
There are three heat transfer modes: conduction, convection, and radiation. In general, each of these three heat transfer modes refers to a separate rate of energy crossing a specific plane, or surface. Often, engineering applications involving heat transfer must consider all three modes in an analysis. In each case, we can write relationships between the rate of heat transfer and temperature. A course in heat transfer is dedicated to calculating the heat transfer in various situations. In thermodynamics, it is given in a problem or it is found from applying the energy equation.
EXAMPLE 3.7
A paddle wheel adds work to a rigid container by rotations caused by dropping a 50-kg weight a distance of 2 m from a pulley. How much heat must be transferred to result in an equivalent effect?
For this non-quasiequilibrium process the work is given by
W = mg × d = 50 × 9.8 × 2 = 980 J
The heat Q that must be transferred equals the work, 980 J.
1. Which work mode is a nonequilibrium work mode?
(A) Compressing a spring
(B) Transmitting torque with a rotating shaft
(C) Energizing an electrical resistor
(D) Compressing gas in a cylinder
2. Ten kilograms of saturated steam at 800 kPa are heated at constant pressure
to 400°C. The work required is nearest
(A) 1150 kJ
(B) 960 kJ
(C) 660 kJ
(D) 115 kJ
3. A stop is located 20 mm above the piston at the position shown. If the mass of the frictionless piston is 64 kg, what work must the air do on the piston so that the pressure in the cylinder increases to 500 kPa?
(A) 22 J
(B) 28 J
(C) 41 J
(D) 53 J
4. Which of the following statements about work for a quasiequilibrium process is incorrect?
(A) The differential of work is inexact
(B) Work is the area under a P-T diagram
(C) Work is a path function
(D) Work is always zero for a constant volume process
Questions 5–8
The frictionless piston shown has a mass of 16 kg. Heat is added until
the temperature reaches 400°C. The initial quality is 20 percent. Assume Patm = 100 kPa.
5. The total mass of the water is nearest
(A) 0.018 kg
(B) 0.012 kg
(C) 0.0014 kg
(D) 0.0010 kg
6. The quality when the piston hits the stops is nearest
(A) 32%
(B) 38%
(C) 44%
(D) 49%
7. The final pressure is nearest
(A) 450 kPa
(B) 560 kPa
(C) 610 kPa
(D) 690 kPa
8. The work done on the piston is nearest
(A) 21 kJ
(B) 28 kJ
(C) 36 kJ
(D) 42 kJ
9. Air is compressed in a cylinder such that the volume changes from
1.2 to 0.02 m3. The initial pressure is 200 kPa. If the pressure is constant, the work is nearest
(A) −36 kJ
(B) −40 kJ
(C) −46 kJ
(D) −52 kJ
10. Estimate the work necessary to compress the air in a cylinder from a pressure of 100 kPa to that of 2000 kPa. The initial volume is 1000 cm3. An isothermal process is to be assumed.
(A) 0.51 kJ
(B) 0.42 kJ
(C) 0.30 kJ
(D) 0.26 kJ
11. Estimate the work done by a gas during an unknown equilibrium process. The pressure and volume are measured as follows:
| P | 200 | 250 | 300 | 350 | 400 | 450 | 500 | kPa |
| V | 800 | 650 | 550 | 475 | 415 | 365 | 360 | cm3 |
(A) 350 J
(B) 260 J
(C) 220 J
(D) 130 J
12. The force needed to compress a nonlinear spring is given by F = 10x2
N, where x is the distance the spring is compressed, measured in meters. Calculate the work needed to compress the spring from 0.2 to 0.8 m.
(A) 0.54 J
(B) 0.72 J
(C) 0.84 J
(D) 0.96 J
13. A paddle wheel and an electric heater supply energy to a system. If the torque is 20 N . m, the rotational speed is 400 rpm, the voltage is 20 V, and the amperage is 10 A, the work rate is nearest
(Α) −820 W
(B) −920 W
(C) −1040 W
(D) −2340 W
14. A gasoline engine drives a small generator that is to supply sufficient
electrical energy for a motor home. What is the minimum horsepower engine that would be necessary if a maximum of 200 A is anticipated from the 12-V system?
(A) 2.4 hp
(B) 2.6 hp
(C) 3.0 hp
(D) 3.2 hp
1. Which of the following does not transfer work to or from a system?
(A) A moving piston
(B) The expanding membrane of a balloon
(C) An electrical resistance heater
(D) A membrane that bursts
2. Ten kilograms of air at 800 kPa are heated at constant pressure from 170 to
400°C. The work required is nearest
(A) 1150 kJ
(B) 960 kJ
(C) 660 kJ
(D) 115 kJ
3.Ten kilograms of saturated liquid water expands until T2 = 200°C while the
pressure remains constant at 400 kPa. Find W 1-2
(A) 2130 kJ
(B) 1960 kJ
(C) 1660 kJ
(D) 1115 kJ
4. A mass of 0.025 kg of steam at a quality of 10 percent and a pressure of 200 kPa is heated in a rigid container until the temperature reaches 300°C.
The pressure at state 2 is nearest
(A) 8.6 MPa
(B) 2.8 MPa
(C) 1.8 MPa
(D) 0.4 MPa
Questions 5–8
The frictionless piston shown in equilibrium has a mass of 64 kg. Energy is added until the temperature reaches 220°C. Assume Patm = 100 kPa.
5. The initial quality is nearest (A) 12.2%
(B) 8.3%
(C) 7.8%
(D) 6.2%
6. The quality when the piston just hits the stops is nearest
(A) 73%
(B) 92%
(C) 96%
(D) 99%
7. The final quality (or pressure if superheat) is nearest
(A) 1.48 MPa
(B) 1.52 MPa
(C) 1.58 MPa
(D) 1.62 MPa
8. The work done on the piston is nearest
(A) 75 J
(B) 96 J
(C) 66 J
(D) 11 J
9. Air is compressed in a cylinder such that the volume changes from 0.2 to 1.2 m3. The pressure at the beginning of the process is 200 kPa. If the
temperature is constant at 50°C, the work is nearest
(A) −133 kJ
(B) −126 kJ
(C) −114 kJ
(D) −92 kJ
10. Air is expanded in a piston-cylinder arrangement at a constant pressure of 200 kPa from a volume of 0.1 m3 to a volume of 0.3 m3. Then the
temperature is held constant during an expansion of 0.5 m3. Determine the
total work done by the air.
(A) 98.6 kJ
(B) 88.2 kJ
(C) 70.6 kJ
(D) 64.2 kJ
11. Air undergoes a three-process cycle. Find the net work done for 2 kg of air if the processes are
1 → 2: constant-pressure expansion
2 → 3: constant volume
3 → 1: constant-temperature compression
The necessary information is T1 = 100°C, T2 = 600°C, and P1 = 200 kPa.
(A) 105 kJ
(B) 96 kJ
(C) 66 kJ
(D) 11.5 kJ
12. A 200-mm-diameter piston is lowered by increasing the pressure from 100 to 800 kPa such that the P-V relationship is PV 2 = const.
| 1 |
If V
= 0.1 m3, the work done on the system is nearest
(A) −18.3 kJ
(B) −24.2 kJ
(C) −31.6 kJ
(D) −42.9 kJ
13. A 120-V electric resistance heater draws 10 A. It operates for 10 min in a rigid volume. Calculate the work done on the air in the volume.
(A) 720 000 kJ
(B) 720 kJ
(C) 12 000 J
(D) 12 kJ
14. An electrical voltage of 110 V is applied across a resistor providing a current of 12 A through the resistor. The work done during a period of 10 min is nearest
(A) 792 000 kJ
(B) 792 kJ
(C) 792 MJ
(D) 792 mJ
Labels: Thermodynamics