Combustion: Combustion Equations ,Enthalpy of Formation, Enthalpy of Combustion, and the First Law and Adiabatic Flame Temperature

Combustion

Several of the devices we have considered in our study of thermodynamics have involved heat transfer from an external source. Most often, the source of the energy supplied by the heat transfer comes from a combustion process, such as in an internal combustion engine or in a power plant. In this chapter, we will consider the process of the combustion of one of the substances included in Table B.6. We will balance the combustion equation, present complete and incomplete combustion, apply the first law with an energy balance, and calculate the temperature of the products of combustion.

9.1 Combustion Equations

Combustion involves the burning of a fuel with oxygen or a substance containing oxygen such as air. A chemical-reaction equation relates the components before and after the chemical process takes place. Let us begin our study of this particular variety of chemical-reaction equations by considering the combustion of propane in a pure oxygen environment. The chemical reaction is represented by

Note that the number of moles of the elements on the left-hand side may not equal the number of moles on the right-hand side. However, the number of atoms of an element must remain the same before, after, and during a chemical reaction; this demands that the mass of each element be conserved during combustion.

In writing the equation, we have demonstrated some knowledge of the products of the reaction. Unless otherwise stated we will assume complete combustion: the

products of the combustion of a hydrocarbon fuel will include H₂O and CO₂ but no CO, OH, C, or H₂ . Incomplete combustion results in products that contain H , CO, C, and/or OH.

For a simple chemical reaction, such as that of Eq. (9.1), we can immediately write down a balanced chemical equation. For more complex reactions the following systematic steps prove useful:

1. Set the number of moles of fuel equal to 1.

2.Balance CO₂ with number of C from the fuel.

3.Balance H₂O with H from the fuel.

4.Balance O₂ from CO₂ and H₂O.

For the combustion of propane in Eq. (9.1), we assumed that the process occurred in a pure oxygen environment. Actually, such a combustion process would normally occur in air. For our purposes we assume that air consists of 21% O₂,and  79% N by volume (we ignore the 1% argon) so that for each mole of O in a reaction we will have

Thus, assuming that N with will not undergo a chemical reaction, Eq. (9.1) is replaced with

The minimum amount of air that supplies sufficient O for complete combustion of the fuel is called theoretical air or stoichiometric air. When complete combustion is achieved with theoretical air, the products contain no CO or O . In practice, it is found that if complete combustion is to occur, air must be supplied in an amount greater than theoretical air. This is due to the chemical kinetics and molecular activity of the reactants and products. Thus, we often speak in terms of percent theoretical air or percent excess air, where they are related by

% theoretical air = 100% + % excess air    (9.4)

Slightly insufficient air results in CO being formed; some hydrocarbons may result from larger deficiencies.

The parameter that relates the amount of air used in a combustion process is the air-fuel ratio (AF), which is the ratio of the mass of air to the mass of fuel. The reciprocal is the fuel-air ratio (FA). Thus

where we have used the molecular weight of air as 29 kg/kmol (close enoughto 28.97) and that of propane as 44 kg/kmol. If, for the combustion of propane,

AF > 15.69, a lean mixture occurs; if AF < 15.69, a rich mixture results.

The combustion of hydrocarbon fuels involves H O in the products of combustion. The calculation of the dew point of the products is often of interest; it is the saturation temperature at the partial pressure of the water vapor. If the temperature drops below the dew point, the water vapor begins to condense. The condensate usually contains corrosive elements, and thus it is often important to ensure that the temperature of the products does not fall below the dew point. This is especially necessary in the chimney of a house; the corrosive elements can eat through the building materials and cause substantial damage. For that reason mid- efficiency furnaces (80% or so) require chimney inserts that are able to resist the corrosive elements.

When analyzing a mixture of gases, either a gravimetric analysis based on mass (or weight) or a volumetric analysis based on moles (or volume) may be used. If the analysis is presented on a dry basis, the water vapor is not included. An Orsat analyzer and a gas chromatograph are two of the devices used to measure the products of combustion.

EXAMPLE 9.1

Butane is burned with dry air at an air-fuel ratio of 20. Calculate the percent excess air, the volume percentage of CO2 in the products, and the dew-point temperature of the products.

Solution

The reaction equation for theoretical air is (see Table B.3 for the composition of butane)

where we have assumed an atmospheric pressure of 100 kPa. Using Table C.2 we find the dew-point temperature to be T_dp= 49°C.

EXAMPLE 9.2

Butane is burned with 90% theoretical air. Calculate the volume percentage of CO in the products and the air-fuel ratio. Assume no hydrocarbons in the products.

Solution

For incomplete combustion we add CO to the products of combustion. Using the reaction equation from Example 9.1,

EXAMPLE 9.3

Butane is burned with dry air, and volumetric analysis of the products on a dry basis (the water vapor is not measured) gives 11.0% CO , 1.0% CO, 3.5% O , and 84.6% N . Determine the percent theoretical air.

Solution

The problem is solved assuming that there are 100 moles of dry products. The chemical equation is

Dividing through the chemical equation by the value of a so that we have 1 mol of fuel, provides

EXAMPLE 9.4

Volumetric analysis of the products of combustion of an unknown hydrocarbon, measured on a dry basis, gives 10.4% CO , 1.2% CO, 2.8% O , and 85.6% N . Determine the composition of the hydrocarbon and the percent excess air.

Solution

The chemical equation for 100 mol dry products is

The chemical formula for the fuel is C_11.6 H_37.9. This could represent a mixture of hydrocarbons, but it is not any species listed in App. B, since the ratio of hydrogen atoms to carbon atoms is 37.9/11.6 = 3.27 = 13/4, i.e., C₄H₁₃.

To find the percent theoretical air we must have the chemical equation using 100% theoretical air. It would be

9.2 Enthalpy of Formation, Enthalpy of Combustion, and the First Law

When a chemical reaction occurs, there may be considerable change in the chemical composition of a system. The problem this creates is that for a control volume the mixture that exits is different from the mixture that enters. Since different zeros are used for enthalpy, it is necessary to establish a standard reference state, chosen as 25°C (77°F) and 1 atm and denoted by the superscript “ o ”, for example, ho. Consider the combustion of H with O , resulting in H₂O:

where the symbol (l) after a chemical compound implies the liquid phase; the symbol (g) would imply the gaseous phase. If no symbol is given, a gas is implied. If and O enter a combustion chamber at 25°C (77°F) and 1 atm and H O(l) leaves the chamber at 25°C (77°F) and 1 atm, then the measured heat transfer will be −285 830 kJ for each kmol of H2O(l) formed. The negative sign on the heat transfer means energy has left the control volume, as shown schematically in Fig. 9.1. The first law applied to a combustion process in a control volume with no shaft work or changes in kinetic and potential energy is

Q = H_P − H_R              (9.8)

where H is the enthalpy of the products of combustion that leave the combustion chamber and H is the enthalpy of the reactants that enter. If the reactants are stable elements, as in our example in Fig. 9.1, and the process is at constant temperature and constant pressure, then the enthalpy change is called the enthalpy of formation, denoted by h_f . The enthalpies of formation of numerous compounds are listed in Table B.5. Note that some compounds have a positive h_f , indicating that they

Figure 9.1 The control volume used during combustion of hydrogen and oxygen.

require energy to form (an endothermic reaction); others have a negative h_f , indicating that they give off energy when they are formed (an exothermic reaction).

The enthalpy of formation is the enthalpy change when a compound is formed. The enthalpy change when a compound undergoes complete combustion at constant temperature and pressure is called the enthalpy of combustion. For example, the enthalpy

of formation of H is zero, and the enthalpy of combustion of H is 285 830 kJ/kmol. Values are listed for several compounds in Table B.6. If the products contain liquid water, the enthalpy of combustion is the higher heating value (HHV); if the products contain water vapor, the enthalpy of combustion is the lower heating value. The difference between the higher heating value and the lower heating value is the heat of vaporization h at standard conditions.If the reactants and products consist of several components, the first law, allow- ing for shaft work but neglecting kinetic and potential energy changes, is

where N represents the number of moles of substance i. The work is often zero, but not in, for example, a combustion turbine.

If combustion occurs in a rigid chamber, like a bomb calorimeter, so that no work results, the first law is.

where we have used enthalpy (u = h – P_v ) since the hi values are tabulated. Since the volume of any liquid or solid is negligible compared to the volume of the gases, we write Eq. (9.10) as

If N_prod= N_react then Q for the rigid volume is equal to Q for the control volume for the isothermal process.

We employ one of the following methods to find (h − h ^o ) :

• For a solid or liquid: Use h − h o = Cp ΔT .

• For gases:

1. Assume an ideal gas with constant specific heat so that h − h = Cp ΔT .

2. Assume an ideal gas and use tabulated values for h.

Which method to use for gases is left to the judgment of the engineer. In our examples, we’ll usually use method 2 for gases with Tables E.1 to E.6 since temperature changes for combustion processes are often quite large and method 1 introduces substantial error.

EXAMPLE 9.5

Calculate the enthalpy of combustion of gaseous propane and of liquid propane assuming the reactants and products to be at 25°C and 1 atm. Assume liquid water in the products exiting the steady-flow combustion chamber.

Solution

Assuming theoretical air (the use of excess air would not influence the result since the process is isothermal), the chemical equation is

This is the enthalpy of combustion; it is stated with the negative sign. The sign is dropped for the HHV; for gaseous propane it is 2220 MJ for each kmol of fuel. For liquid propane we find

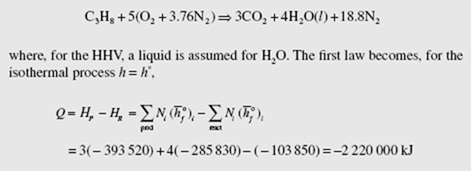
Q = 3( − 393 520) + 4( − 285 830) − ( − 103 850 − 15 060) = − 2 205 000 kJ

This is slightly less than the HHV for gaseous propane, because some energy is

needed to vaporize the liquid fuel.

EXAMPLE 9.6

Calculate the heat transfer required if propane and air enter a steady-flow combustion chamber at 25°C and 1 atm and the products leave at 600 K and 1 atm. Use theoretical air and one mole of fuel.

Solution

The combustion equation is written using H O in the vapor form due to the high

exit temperature:

where we have used method 2 listed for gases. This heat transfer is less than the

enthalpy of combustion of propane, as it should be, since some energy is needed to heat the products to 600 K.

EXAMPLE 9.7

Liquid octane at 25°C fuels a jet engine. Air at 600 K enters the insulated combustion chamber and the products leave at 1000 K. The pressure is assumed constant at 1 atm. Estimate the exit velocity using theoretical air.

Solution

The equation is

For the reactants,

EXAMPLE 9.8

Liquid octane is burned with 300% excess air. The octane and air enter the steady-flow combustion chamber at 25°C and 1 atm and the products exit at 1000 K and 1 atm. Estimate the heat transfer for one mole of fuel.

Solution

The reaction with theoretical air is

EXAMPLE 9.9

A constant-volume bomb calorimeter is surrounded by water at 20°C. One mole of liquid propane is burned with pure oxygen in the calorimeter. Determine the heat transfer to be expected.

Solution

The complete combustion of propane follows:

The surrounding water sustains a constant-temperature process, so that Eq. (9.11) becomes

9.3 Adiabatic Flame Temperature

If we consider a combustion process that takes place adiabatically, with no work or changes in kinetic and potential energy, then the temperature of the products is referred to as the adiabatic flame temperature. The maximum adiabatic flame temperature that can be achieved occurs at theoretical air. This fact allows us to control the adiabatic flame temperature by the amount of excess air involved in the process: the greater the excess air, the lower the adiabatic flame temperature. If the blades in a turbine can withstand a certain maximum temperature, we can determine the excess air needed so that the maximum allowable blade temperature is not exceeded. We will find that an iterative (trial-and-error) procedure is needed to find the adiabatic flame temperature. A quick approximation to the adiabatic flame temperature is found by assuming the products to be completely N . An example will illustrate.

The adiabatic flame temperature is calculated assuming complete combustion, no heat transfer from the combustion chamber, and no dissociation of the products into other chemical species. Each of these effects tends to reduce the adiabatic flame temperature. Consequently, the adiabatic flame temperature that we will calculate represents the maximum possible flame temperature for the specified percentage of theoretical air.

If a significant amount of heat transfer does occur from the combustion chamber, we can account for it by including the following term in the energy equation:

EXAMPLE 9.10

Propane is burned with 250% theoretical air; both are at 25°C and 1 atm. Predict the adiabatic flame temperature in the steady-flow combustion chamber.

Solution

The combustion with theoretical air is

Since Q = 0 for an adiabatic process we demand that HR = HP. The enthalpy of the reactants, at 25°C, is H = −103 850 kJ.

The temperature of the products is unknown; and we cannot obtain the enthalpies of the components of the products from the tables without knowing the temperatures. This requires a trial-and-error solution. To obtain an initial guess, we assume the products to be composed entirely of nitrogen:

where we have noted that the products contain 61.5 mol of gas (at 25^oC, h = 8670 kJ/kmol from Table E.2). This gives h = 43 400 kJ/kmol, which suggests a temperature of about 1380 K (take T a little less than that predicted by the all-nitrogen assumption). Using this temperature we check using the actual products:

We use the above two results for 1380 and 1300 K and, assuming a linear relationship, predict that

EXAMPLE 9.11

Propane is burned with theoretical air; both are at 25°C and 1 atm in a steady- flow combustion chamber. Predict the adiabatic flame temperature.

Solution

The combustion with theoretical air is

For the adiabatic process the first law takes the form H_R = H_P. Hence, assuming the products to be composed entirely of nitrogen,

−103 850 = 3( − 393 520) + 4( − 241 820) + 25.8(h_P − 8670)

where the products contain 25.8 mol gas. This gives h = 87 900 kJ/kmol, which suggests a temperature of about 2600 K. With this temperature we find, using the actual products:

−103 850 = 3(−393 520 + 137 400 − 9360) + 4(−241 820 + 114 300 − 9900)

+ 18.8(86 600 − 8670) = 119 000

At 2400 K there results

−103 850 = 3(−393 520 + 125 200 − 9360) + 4(−241 820 + 103 500 − 9900)

+ 18.8(79 320 − 8670) = −97 700

A straight line extrapolation gives T_p = 2394 K.

Quiz No. 1

1. The fuel C₄ H₁₀ combines with stoichiometric air. Provide the correct values for x, y, z in the reaction C₄ H₁₀ + w(O₂ + 3.76N₂ ) → xCO₂ + yH₂O + zN₂.

(A) (4, 5, 24.44)

(B) (5, 6, 30.08)

(C) (4, 10, 24.44)

(D) (5, 10, 24.44)

2.Methane (CH₄ ) is burned with stoichiometric air and the products are cooled to 20°C assuming complete combustion at 100 kPa. Calculate the air-fuel ratio.

(A) 16.9

(B) 17.2

(C) 17.8

(D) 18.3

3. For the combustion of the methane of Prob. 2, what is the percentage of CO by weight in the products?

(A) 15.1%

(B) 17.2%

(C) 18.1%

(D) 18.5%

4. For the reaction of the methane of Prob. 2, the dew-point temperature of the products is nearest

(A) 48°C

(B) 54°C

(C) 57°C

(D) 59°C

5. Ethane (C H ) undergoes complete combustion at 95 kPa with 180% theoretical air. Find the air-fuel ratio.

(A) 23

(B) 25

(C) 27

(D) 29

6.For the combustion of the ethane of Prob. 5, what is the percentage of CO by weight in the products?

(A) 5.83%

(B) 6.35%

(C) 8.61%

(D) 11.7%

7.Calculate the mass flow rate of methane (CH ) required if the inlet air flow rate is 20 m3/min at 20°C and 100 kPa using stoichiometric air.

(A) 4.32 kg/min

(B) 2.87 kg/min

(C) 1.38 kg/min

(D) 1.09 kg/min

8. An air-fuel ratio of 25 is used in an engine that burns octane (C H ). Find

the percentage of excess air required. (A) 65.4%

(B) 69.4%

(C) 72.4%

(D) 76.4%

9. Carbon reacts with oxygen to form carbon dioxide in a steady-flow chamber. Calculate the energy involved. Assume the reactants and products are at 25°C and 1 atm.

(A) −399 300 kJ/kmol

(B) −393 500 kJ/kmol

(C) −389 300 kJ/kmol

(D) −375 200 kJ/kmol

10. Liquid propane (C H ) undergoes combustion with air; both are at 25°C and 1 atm. Calculate the heat transfer if the products from a steady-flow combustor are at 1000 K with 100% theoretical air.

(A) 1.44 × 106 kJ/kmol
(B) 1.65 × 106 kJ/kmol
(C) 1.79 × 106 kJ/kmol
(D) 1.93 × 106 kJ/kmol

Quiz No. 2

1. The fuel C₅ H₁₂ combines with stoichiometric air. Provide the correct values for x, y, z in the reaction C₅H₁₂ + w(O₂ + 3.76N₂ ) → xCO₂ + yH₂O + zN₂.

(A) (4, 5, 24.44)

(B) (5, 6, 30.08)

(C) (5, 12, 30.08)

(D) (4, 12, 30.08)

2. Ethane (C₂H₆) is burned with stoichiometric air and the products are cooled to 20°C assuming complete combustion at 100 kPa. Calculate the air-fuel ratio.

(A) 17.9

(B) 17.2

(C) 16.8

(D) 16.1

3.For the combustion of the ethane of Prob. 2, what is the percentage of CO by weight in the products?

(A) 15.1%

(B) 17.2%

(C) 18.1%

(D) 18.5%

4. For the reaction of the ethane of Prob. 2, the dew-point temperature of the products is nearest

(A) 48°C

(B) 54°C

(C) 56°C

(C) 59°C

5. Propane (C H ) undergoes complete combustion at 95 kPa with 180% theoretical air. The air-fuel ratio is nearest.

(A) 28.2

(B) 26.1

(C) 24.9

(D) 22.5

6. For the combustion of the propane of Prob. 5, what is the percentage of CO₂ by weight in the products?

(A) 5.83%

(B) 6.35%

(C) 6.69%

(C) 7.94%

7. Calculate the mass flow rate of propane (C H ) required if the inlet air flow rate is 20 m3/min at 20°C and 100 kPa using stoichiometric air.

(A) 2.70 kg/min

(B) 1.93 kg/min

(C) 1.79 kg/min

(D) 1.52 kg/min

8. Butane (C H ) is burned with 50% excess air. If 5% of the carbon in the fuel is converted to CO, calculate the air-fuel ratio.

(A) 23.2

(B) 25.8

(C) 27.1

(D) 29.9

9. Hydrogen reacts with oxygen to form water vapor in a steady-flow chamber. Calculate the energy involved. Assume the reactants and products are at 25°C and 1 atm.

(A) 376 700 kJ/kmol

(B) 483 600 kJ/kmol

(C) 523 900 kJ/kmol

(D) 587 800 kJ/kmol

10. Liquid propane (C3H8) undergoes complete combustion with air; both are at 25°C and 1 atm. Calculate the heat transfer if the products from a steady- flow combustor are at 1000 K and the percent theoretical air is 200%.

(A) 1.18 × 106 kJ/kmol
(B) 1.45 × 106 kJ/kmol
(C) 1.69 × 106 kJ/kmol
(D) 1.83 × 106 kJ/kmol

Labels: Thermodynamics