Compressible flows occur when the density changes are significant between two points on a streamline. Not all gas flows are compressible flows, only those that have significant density changes. Flow around automobiles, in hurricanes, around aircraft during landing and takeoff, and around buildings are a few examples of incompressible flows in which the density of the air does not change more than 3 percent between points of interest and are consequently treated as incompressible flows. There are, however, many examples of gas flows in which the density does change significantly; they include airflow around aircraft that fly faster than a Mach number [see Eq. (3.18)] of 0.3 (about 100 m/s), through compressors, jet engines, and tornados. Not considered in this chapter are compressible effects in liquid flows that give rise to water hammer and underwater compression waves from blasts.
Only compressible flow problems that can be solved using the integral equations will be considered in this chapter. The simplest of these is uniform flow in a conduit. Recall that the continuity equation, the momentum equation, and the energy equation (no work or heat transfer) are, respectively,
where the enthalpy h = u- + p/ρ is used. If the gas can be approximated as an ideal gas, then the energy equation takes either of the following two forms:
Recall that the temperatures and pressures must always be absolute quantities when using several of the above relations. It is always safe to use absolute temperature and pressure when solving problems involving a compressible flow.
9.2 Speed of Sound
A pressure wave with small amplitude is called a sound wave and it travels through a gas with the speed of sound, denoted by c. Consider the small-amplitude wave shown in Fig. 9.1 traveling through a conduit. In Fig. 9.2a it is moving so that a stationary observer sees an unsteady motion; in Fig. 9.2b the observer moves with the wave so that the wave is stationary and a steady flow is observed; Fig. 9.2c shows the control volume surrounding the wave. The wave is assumed to create a small differential change in the pressure p, the temperature T, the density r, and the velocity V in the gas. The continuity equation applied to the control volume provides
Combining the continuity and momentum equations results in
The lower-frequency (less than 18 000 Hz) sound waves travel isentropically so that p/r k = const which, when differentiated, gives
The Mach number, introduced in Chap. 3, is used for disturbances moving in a gas. It is
EXAMPLE 9.1
An electronic device is situated on the top of a hill and hears a supersonic projectile that produces Mach waves after the projectile is 500 m past the device’s position. If it is known that the projectile flies at 850 m/s, estimate how high it is above the device.
Solution
The Mach number is
where a standard temperature of 288 K has been assumed since the temperature was not given. The Mach angle relationship allows us to write
where h is the height above the device (refer to Fig. 9.2c). This equation can be solved for h to give
h = 218 m
9.3 Isentropic Nozzle Flow
There are numerous applications where a steady, uniform, isentropic flow is a good approximation to the flow in conduits. These include the flow through a jet engine, through the nozzle of a rocket, from a broken gas line, and past the blades of a turbine. To model such situations, consider the control volume in the changing area of the conduit of Fig. 9.3. The continuity equation between two sections an infinitesimal distance dx apart is
This simplifies to, neglecting higher-order terms,
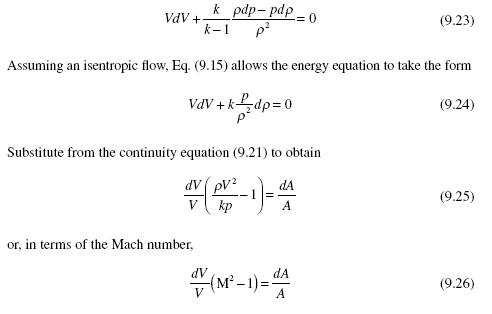
There are several observations that can be made from an analysis of Eq. (9.26). They are:
• For a subsonic flow in an expanding conduit (M < 1 and dA > 0), the flow is decelerating (dV < 0).
• For a subsonic flow in a converging conduit (M < 1 and dA < 0), the flow is accelerating (dV > 0).
• For a supersonic flow in an expanding conduit (M > 1 and dA > 0), the flow is accelerating (dV > 0).
• For a supersonic flow in a converging conduit (M > 1 and dA < 0), the flow is decelerating (dV < 0).
• At a throat where dA = 0, either M = 1 or dV = 0 (the flow could be accelerating through M = 1, or it may reach a velocity such that dV = 0).
Observe that a nozzle for a supersonic flow must increase in area in the flow direction, and a diffuser must decrease in area, opposite to a nozzle and diffuser for a subsonic flow. So, for a supersonic flow to develop from a reservoir where the velocity is zero, the subsonic flow must first accelerate through a converging area to a throat, followed by continued acceleration through an enlarging area.
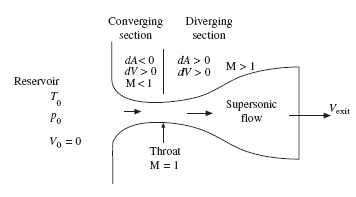
The nozzles on a rocket designed to place satellites in orbit are constructed using such converging-diverging geometry, as shown in Fig. 9.4.
The energy and continuity equations can take on particularly helpful forms for the steady, uniform, isentropic flow through the nozzle of Fig. 9.4. Apply the energy
equation (9.4) with nozzle to obtain
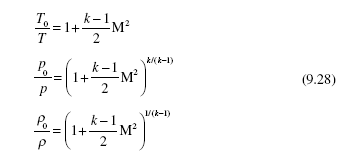
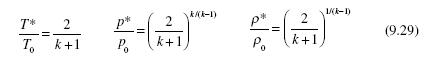
D.1. For air with k = 1.4, the equations above provide
This ratio is included in the isentropic flow Table D.1 for air. The table can be used in place of the above equations.
Now we will discuss some features of the above equations. Consider a converging nozzle connecting a reservoir with a receiver, as shown in Fig. 9.5. If the reservoir pressure is held constant and the receiver pressure reduced, the Mach number at the exit of the nozzle will increase until M = 1 is reached, indicated by the left curve in the figure. After M = 1 is reached at the nozzle exit for pr = 0.5283p0, the condition of choked flow occurs and the velocity throughout the nozzle cannot change with further decreases in p . This is due to the fact that pressure changes downstream of the exit cannot travel upstream to cause changes in the flow conditions.
The right curve of Fig. 9.5b represents the case when the reservoir pressure is increased and the receiver pressure is held constant. When M = 1, the condition of choked flow also occurs; but Eq. (9.33) indicates that the mass flux will continue to increase as p is increased. This is the case when a gas line ruptures.
It is interesting that the exit pressure p is able to be greater than the receiver pressure p . Nature allows this by providing the streamlines of a gas the ability to make a sudden change of direction at the exit and expand to a much greater area resulting in a reduction of the pressure from p to p . The case of a converging-diverging nozzle allows a supersonic flow to occur, providing the receiver pressure is sufficiently low. This is shown in Fig. 9.6 assuming a constant reservoir pressure with a decreasing receiver pressure. If the receiver pressure
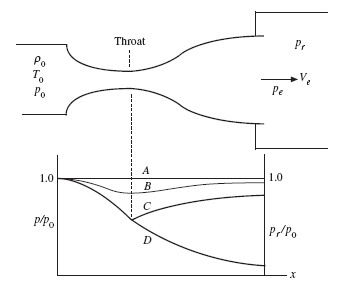
is equal to the reservoir pressure, no flow occurs, represented by curve A. If p is slightly less than p , the flow is subsonic throughout, with a minimum pressure at the throat, represented by curve B. As the pressure is reduced still further, a pressure is reached that results in M = 1 at the throat with subsonic flow throughout the remainder of the nozzle.
There is another receiver pressure substantially below that of curve C that also results in isentropic flow throughout the nozzle, represented by curve D; after the throat the flow is supersonic. Pressures in the receiver in between those of curve C and curve D result in non-isentropic flow (a shock wave occurs in the flow) and will be considered in the next section. If p is below that of curve D, the exit pressure p is greater than p . Once again, for receiver pressures below that of curve C, the mass flux remains constant since the conditions at the throat remain unchanged.
It may appear that the supersonic flow will tend to separate from the nozzle, but just the opposite is true. A supersonic flow can turn very sharp angles, as will be observed in Sec. 9.6, since nature provides expansion fans that do not exist in subsonic flows. To
avoid separation in subsonic nozzles, the expansion angle should not exceed 10°. For larger angles, vanes are used so that the angle between the vanes does not exceed 10°.
EXAMPLE 9.2
Air flows from a reservoir maintained at 300 kPa absolute and 20°C into a receiver
maintained at 200 kPa absolute by passing through a converging nozzle with an
exit diameter of 4 cm. Calculate the mass flux through the nozzle. Use (a) the equations and (b) the isentropic flow table.
Solution
(a) The receiver pressure that would give M = 1 at the nozzle exit is
For the units to be consistent, the pressure must be in Pa and R in J/kg · K.
(b) Now use Table D.1. For a pressure ratio of p/p0 = 200/300 = 0.6667, the Mach mnumber is found by interpolation to be
To find the mass flux the velocity must be known which requires the temperature
since 
Labels: Fluid mechanics
