 Figure 9.7 A stationary shock wave.
Figure 9.7 A stationary shock wave.9.1 Normal Shock Waves
Shock waves are large-amplitude waves that travel in a gas. They emanate from the wings of a supersonic aircraft, from a large explosion, from a jet engine, and ahead of the projectile in a gun barrel. They can be oblique waves or normal waves. First, we will consider the normal shock wave, as shown in Fig. 9.7. In this figure it is stationary so that a steady flow exists. If V1 were superimposed to the left, the shock

would be traveling in stagnant air with velocity V and the induced velocity behindthe shock wave would be (V1– V2). The shock wave is very thin, on the order of 10−4 mm, and in that short distance large pressure changes occur causing enormous energy dissipation. The continuity equation with A1= A2 is

Rather than solve the above three equations simultaneously, we write them in terms of the Mach numbers M and M , and put them in more convenient forms.
First, the momentum equation (9.37), using Eq. (9.35) and V 2 = M2 pk /ρ, can be written as
In like manner, the energy equation (9.36), with p = ρRT and V 2 = M2 kRT , can be written as




Return to the converging-diverging nozzle and focus attention on the flow below curve C of Fig. 9.6. If the receiver pressure decreases to p /p = a in Fig. 9.8, a normal r 0 shock wave would be positioned somewhere inside the nozzle as shown. If the receiver pressure decreased still further, there would be some ratio p /p = b that would posi- r 0 tion the shock wave at the exit plane of the nozzle. Pressure ratios c and d would result in oblique shock-wave patterns similar to those shown. Pressure ratio e is associated with isentropic flow throughout, and pressure ratio f would provide an exit pressure greater than the receiver pressure resulting in a billowing out, as shown, of the exiting flow, as seen on the rockets that propel satellites into space.
EXAMPLE 9.3
A normal shock wave travels at 600 m/s through stagnant 20°C air. Estimate the velocity induced behind the shock wave. (a) Use the equations and (b) use the normal shock-flow table D.2. Refer to Fig. 9.7.
Solution
Superimpose a velocity of 600 m/s so that the shock wave is stationary and V1 = 600 m/s, as displayed in Fig. 9.7. The upstream Mach number is
(a) Using the equations, the downstream Mach number and temperature are, respectively,
Air flows from a reservoir maintained at 20°C and 200 kPa absolute through a converging-diverging nozzle with a throat diameter of 6 cm and an exit diameter of 12 cm to a receiver. What receiver pressure is needed to locate a shock wave at a position where the diameter is 10 cm? Refer to Fig. 9.8.
Let’s use the isentropic-flow table D.1 and the normal shock-flow table D.2. At the throat for this supersonic flow M = 1. The Mach number just before the shock wave is interpolated from Table D.1 where A1 /A* = 10 /6 = 2.778 to be
since the stagnation pressure does not change in the isentropic flow before the shock wave so that p01 = 200 kPa. From just after the shock wave to the exit, isentropic flow again exists so that from Table D.1 at M = 0.5078

Using Table D.1 at this area ratio (make sure the subsonic part of the table is used), we find
using p0 e = p02 for the isentropic flow after the shock wave. The exit pressure is equal to the receiver pressure for this isentropic subsonic flow.
9.2 Oblique Shock Waves
Oblique shock waves form on the leading edge of a supersonic sharp-edged airfoil or in a corner, as shown in Fig. 9.9. A steady, uniform plane flow exists before and after the shock wave. The oblique shock waves also form on axisymmetric projectiles.
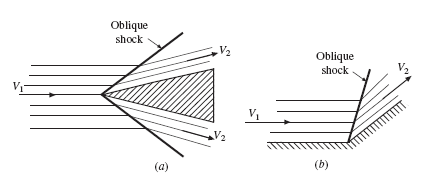
The oblique shock wave turns the flow so that V2 is parallel to the plane surface.
Another variable, the angle through which the flow turns, is introduced but the additional tangential momentum equation allows a solution. Consider the control volume of Fig. 9.10 surrounding the oblique shock wave. The velocity vector V1 is assumed to be in the x-direction and the oblique shock wave turns the flow through the wedge angle or deflection angle q so that V2 is parallel to the wall. The oblique shock wave makes an angle of b with V1. The components of the velocity vectors are shown normal and tangential to the oblique shock. The tangential components of the velocity vectors do not cause fluid to flow into or out of the control volume, so continuity providesThe pressure forces act normal to the control volume and produce no net force tan- gential to the oblique shock. This allows the tangential momentum equation to take the form


Observe that the tangential velocity components do not enter the three Eqs. (9.45), (9.48), and (9.49). They are the same three equations used to solve the normal shock- wave problem. So, the components V1n and V2n can be replaced with V1 and V2, respectively, of the normal shock-wave problem and a solution obtained. Table D.2 may also
To often simplify a solution, we relate the oblique shock angle b to the deflection angle q. This is done by using Eq. (9.45) to obtain
With this relationship the oblique shock angle b can be found for a given incoming Mach number and wedge angle q. A plot of Eq. (9.52) is useful to avoid a trial-and- error solution. It is included as Fig. 9.11. Three observations can be made by studying the figure.
Figure 9.11 Οblique shοck wave angle b related tο wedge angle q and Mach
For given Mach number M and wedge angle q there are two possible oblique shock angles b. The larger one is the “strong” oblique shock wave and the smaller one is the “weak” oblique shock wave.
• For a given wedge angle q there is a minimum Mach number for which there is only one oblique shock angle b.
• If the Mach number is less than the minimum for a particular q, but greater than one, the shock wave is detached as shown in Fig. 9.12. Also, for a given M1 there is a sufficiently large q that will result in a detached
shock wave.
The required pressure rise determines if a weak shock or a strong shock exists. The pressure rise is determined by flow conditions.
For a detached shock wave around a blunt body or a wedge, a normal shock wave exists on the stagnation streamline; the normal shock is followed by a strong oblique shock, then a weak oblique shock, and finally a Mach wave, as shown in Fig. 9.12. The shock wave is always detached on a blunt object.
Figure 9.12 Detached shock waves around (a) a plane, blunt object and (b) a wedge.
EXAMPLE 9.5
Air at 30°C flows around a wedge with an included angle of 60° (see Fig. 9.9a). An oblique shock emanates from the wedge at an angle of 50°. Determine the approach velocity of the air. Also find M and T .
Solution
![image_thumb[5] image_thumb[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEguFg-asB2-jhQ1X6TbV5xcfxl0mIlq2R4v92fVCZm62w_c0dyXDEhay57FUVqwz8xTH_rlV1GBqYUjPHifHJRYSOvQ-0stKfMYIkh2juvTdRZl9NNhRwuy9P6iqUl6XmE0-Bc0fdJzlPWM/?imgmax=800)
9.3 Expansion Waves
Supersonic flow exits a nozzle (the pressure ratio f in Fig. 9.8), and billows out into a large exhaust plume. Also, supersonic flow does not separate from the wall of a nozzle that expands quite rapidly, as shown in Fig. 9.8. How is this accomplished? Consider the possibility that a single finite wave, such as an oblique shock, is able to turn the flow around the convex corner, as shown in Fig. 9.13a. From the tangential momentum equation, the tangential component of velocity must remain the same on both sides of the finite wave. For this to be true, V2 > V1. As before, this increase in velocity as the fluid flows through a finite wave requires an increase in entropy, a violation of the second law of thermodynamics, making a finite wave an impossibility.
A second possibility is to allow an infinite fan of Mach waves, called an expansion fan, emanating from the corner, as shown in Fig. 9.13b. This is an ideal isentropic process so the second law is not violated; such a process may be approached in a real application. Let’s consider the single infinitesimal Mach wave displayed in Fig. 9.14, apply our fundamental laws, and then integrate around the corner. Since the tangential velocity components are equal, the velocity triangles yield
![image_thumb[7] image_thumb[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgyzK9R6L_5i3ifgN-DjV1HQ2Zlmml5aPHK5g4Ept434qlXuMNGZW4eeR9IIJfiW1oAO7qpRMflg-dCTDBkUaG3dqDylW7yKY4WQWgOZ8hNh4bDq7PHy5t-exkJBhQPkH3fKOBIU_-ema8S/?imgmax=800)
The solution to this relationship is presented for air in Table D.3 to avoid a trial-and- error solution for M given the angle q. If the pressure or temperature is desired, the isentropic flow table can be used. The Mach waves that allow the gas to turn the corner are sometimes referred to as expansion waves.
Observe from Table D.3 that the expansion fan that turns the gas through the angle q results in M = 1 before the fan to a supersonic flow after the fan. The gas
speeds up as it turns the corner and it does not separate. A slower moving subsonic flow would separate from the corner and would slow down. If M = ∞ is substituted into Eq. (9.60), θ = 130.5°, which is the maximum angle through which the flow could possibly turn. This shows that turning angles greater than 90° are possible, a rather surprising result.
EXAMPLE 9.6
Air at 150 kPa and 140°C flows at M = 2 and turns a convex corner of 30°. Estimate
the Mach number, pressure, temperature, and velocity after the corner.
Solution
Table D.3 assumes the air is initially at M = 1. So, assume the flow originates from M = 1 and turns a corner to M1 = 2 and then a second corner to M2, as shown. From Table D.3, an angle of 26.4° is required to accelerate the flow from M = 1 to M = 2. Add another 30° to 26.4° and at q = 56.4° we find that
M2 = 3.37
Using the isentropic flow table D.1, the entries from the reservoir to state 1 and also to state 2 can be used to find
Quiz No. 1
1. Two rocks are slammed together by a friend on one side of a lake. A listening device picks up the wave generated 0.45 s later. The distance across the lake is nearest
(A) 450 m
(B) 550 m
(C) 650 m
(D) 750 m
2. The Mach number for a projectile flying at 10 000 m at 200 m/s is (A) 0.62
(B) 0.67
(C) 0.69
(D) 0.74
3. A supersonic aircraft passes 200 m overhead on a day when the temperature is 26°C. Estimate how far the aircraft is from you when you hear its sound if its Mach number is 1.68.
(A) 245 m
(B) 275 m
(C) 315 m
(D) 335 m
4. A converging nozzle with exit area of 10 cm2 is attached to a reservoir maintained at 250 kPa absolute and 20°C. If the receiver pressure is maintained at 150 kPa absolute, the mass flux is nearest
(A) 0.584 kg/s
(B) 0.502 kg/s
(C) 0.428 kg/s
(D) 0.386 kg/s
5. Air flows through a converging-diverging nozzle attached from a reservoir maintained at 400 kPa absolute and 20°C to a receiver. If the throat and exit diameters are 10 and 24 cm, respectively, the receiver pressure that will just result in supersonic flow throughout is nearest
(A) 6.8 kPa
(B) 9.2 kPa
(C) 16.4 kPa
(D) 28.2 kPa
6. The temperature, pressure, and velocity before a normal shock wave in air are 18°C, 100 kPa absolute, and 600 m/s, respectively. The velocity after the shock wave is nearest
(A) 212 m/s
(B) 249 m/s
(C) 262 m/s
(D) 285 m/s
7. A large explosion occurs on the earth’s surface producing a shock wave that travels radially outward. At a particular location the Mach number of the wave is 2.0. Determine the induced velocity behind the shock wave if T1 = 15°C.
(A) 502 m/s
(B) 425 m/s
(C) 368 m/s
(D) 255 m/s
8. Air flows from a reservoir through a nozzle into a receiver. The reservoir is maintained at 400 kPa absolute and 20°C. The nozzle has a 10-cm-diameter throat and a 20-cm-diameter exit. The receiver pressure needed to locate a shock wave at the exit is nearest
(A) 150 kPa
(B) 140 kPa
(C) 130 kPa
(D) 120 kPa
(A) 164 kPa
(B) 181 kPa
(C) 192 kPa
(D) 204 kPa
10. An airflow with a Mach number of 2.4 turns a convex corner of 40°. If the temperature and pressure are 5°C and 60 kPa absolute, respectively, the Mach number after the corner is nearest
(A) 5
(B) 3
(C) 2
(D) 1
Quiz No. 2
1. An underwater animal generates a signal that travels through water until it hits an object and then echoes back to the animal 0.46 s later. How far is the animal from the object?
2. A bolt of lightning lights up the sky and 1.5 s later you hear the thunder.
How far did the lightning strike from your position?
3. A supersonic aircraft passes 200 m overhead on a day when the temperature is 26°C. Estimate how far the aircraft is from you when you hear its sound if its Mach number is 3.49.
4. A small-amplitude wave travels through the 15°C atmosphere creating a pressure rise of 5 Pa. Estimate the temperature rise across the wave and the induced velocity behind the wave.
5. A converging nozzle with exit area of 10 cm2 is attached to a reservoir maintained at 250 kPa absolute and 20°C. Calculate the mass flux if the receiver pressure is maintained at 100 kPa absolute.
6. Air flows from a converging-diverging nozzle from a reservoir maintained at 400 kPa absolute and 20°C through a 12-cm-diameter throat. At what diameter in the diverging section will M = 2?
7. The temperature and pressure before a normal shock wave in air are 20°C and 400 kPa absolute, respectively. The Mach number after the shock wave is 0.5. Calculate the pressure and velocity after the shock.
8. Air flows from a reservoir maintained at 400 kPa absolute and 20°C out a nozzle with a 10-cm-diameter throat and a 20-cm-diameter exit into a
receiver. Estimate the receiver pressure needed to locate a shock wave at a diameter of 16 cm.
9. A supersonic airflow changes direction 20° due to a sudden corner (see Fig. 9.9b). If T1 = 40°C, p1 = 60 kPa absolute, and V1 = 900 m/s, calculate p and V assuming a strong shock.
10. An airflow with M = 3.6 is desired by turning a 20°C-supersonic flow with a Mach number of 1.8 around a convex corner. If the upstream pressure is 40 kPa absolute, what angle should the corner possess? What is the velocity after the corner?
Labels: Fluid mechanics