 The velocity ratio would be found by equating the Reynolds numbers:
The velocity ratio would be found by equating the Reynolds numbers:6.1 Similitude
After the dimensionless parameters have been identified and a study on a model has been accomplished in a laboratory, similitude allows us to predict the behavior of a prototype from the measurements made on the model. The measurements on the model of a ship in a towing basin or on the model of an aircraft in a wind tunnel are used to predict the performance of the ship or the aircraft.
The application of similitude is based on three types of similarity. First, a model must look like the prototype, that is, the length ratio must be constant between corresponding points on the model and prototype. For example, if the ratio of the lengths of the model and prototype is l, then every other length ratio is also l. Hence, the area ratio would be l2 and the volume ratio l3. This is geometric similarity.
The second is dynamic similarity: all force ratios acting on corresponding mass elements in the model flow and the prototype flow are the same. This results by equating the appropriate dimensionless numbers of Eq. (6.17). If viscous effects are important, the Reynolds numbers are equated; if compressibility is significant, Mach numbers are equated; if gravity influences the flows, Froude numbers are equated; if an angular velocity influences the flow, the Strouhal numbers are equated; and, if surface tension affects the flow, the Weber numbers are equated. All of these numbers can be shown to be ratios of forces so equating the numbers in a particular flow is equivalent to equating the force ratios in that flow.
The third type of similarity is kinematic similarity: the velocity ratio is the same between corresponding points in the flow around the model and the prototype.
Assuming complete similarity between model and prototype, quantities of interest can now be predicted. For example, if a drag force is measured on flow around a model in which viscous effects play an important role, the ratio of the forces [see Eq. (6.18)] would be

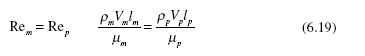
It would be

If the Froude number governed the study, we would have
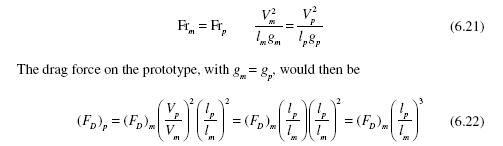
cannot satisfy both the Reynolds number and the Froude number in a study if the same fluid is used for the model study as exists in the prototype flow; the model study of a ship always uses water as the fluid. To account for the viscous drag, the results of the model study based on the Froude number are adapted using industrial modifiers not included in an introductory fluids course.
EXAMPLE 6.3
A clever design of the front of a ship is to be tested in a water basin. A drag of
12.2 N is measured on the 1:20 scale model when towed at a speed of 3.6 m/s. Determine the corresponding speed of the prototype ship and the drag to be expected.
Solution
The Froude number guides the model study of a ship since gravity effects (wave motions) are more significant than the viscous effects. Consequently,
To find the drag on the prototype, the drag ratio is equated to the gravity force ratio (the inertial force ratio could be used but not the viscous force ratio since viscous forces have been ignored):
where we used Pm = rp since salt water and fresh water have nearly the same density. The above results would be modified based on established factors to account for the viscous drag on the ship.
EXAMPLE 6.4
A large pump delivering 1.2 m3/s of water with a pressure rise of 400 kPa is needed for a particular hydroelectric power plant. A proposed design change is tested on a smaller 1:4 scale pump. Estimate the flow rate and pressure rise that
would be expected in the model study. If the power needed to operate the model pump is measured to be 8000 kW, what power would be expected to operate the prototype pump?
Solution
For this internal flow problem, Reynolds number would be equated:
This is an unexpected result. When using the Reynolds number to guide a model study, the power measured on the model exceeds the power needed to operate the prototype since the pressures are so much larger on the model. Note that in this example the Euler number would be used to provide the model pressure rise as
For this reason and the observation that the velocity is much larger on the model, model studies are not common for situations (e.g., flow around an automobile) in which the Reynolds number is the guiding parameter.
EXAMPLE 6.5
The pressure rise from free stream to a certain location on the surface of the model of a rocket is measured to be 22 kPa at an air speed of 1200 km/h. The
wind tunnel is maintained at 90 kPa absolute and 15°C. What would be the speed
and pressure rise on a rocket prototype at an elevation of 15 km?
Solution
The Mach number governs the model study. Thus,
Quiz No. 1
1. If the F-L-T system is used, the dimensions on density are:
(A) FT /L2
(B) FT 2/L2
(C) FT /L4
(D) FT 2/L4
2. Combine the angular velocity w, viscosity m, diameter d, and density r into a single dimensionless group, a p term.
(A) ωρb/μ
(B) ωρb4/μ
(C) ωρb2/μ
(D) ω 2 ρb/μ
3. What variable could not influence the velocity if it is proposed that the velocity depends on a diameter, a length, gravity, rotational speed, and viscosity?
(A) Gravity
(B) Rotational speed
(C) Viscosity
(D) Diameter
4. It is proposed that the velocity V issuing from a hole in the side of an open tank depends on the density r of the fluid, the distance H from the surface, and gravity g. What expression relates the variables?
5. Add viscosity to the variables in Prob. 4. Rework the problem.

7. A new design is proposed for an automobile. It is suggested that a 1:5 scale model study be done to access the proposed design for a speed of 90 km/h. What speed should be selected for the model study, based on the appropriate parameter?
(A) 500 km/h
(B) 450 km/h
(C) 325 km/h
(D) 270 km/h
8. A proposed pier design is studied in a water channel to simulate forces due to hurricanes. Using a 1:10 scale model, what velocity should be selected in the model study to simulate a water speed of 12 m/s?
(A) 3.79 m/s
(B) 4.28 m/s
(C) 5.91 m/s
(D) 6.70 m/s
9. The force on a weir is to be predicted by studying the flow of water over a 1:10 scale model. If 1.8 m3/s is expected over the weir, what flow rate should be used in the model study?
(A) 362 m3/s
(B) 489 m3/s
(C) 569 m3/s
(D) 674 m3/s
10. What force should be expected on the weir of Prob. 9 if 20 N is measured on the model?
(A) 15 kN
(B) 20 kN
(C) 25 kN
(D) 30 kN
Quiz No. 2
1. If the F-L-T system is used, what are the dimensions on viscosity?
2. Combine power W·, diameter d, velocity V, and pressure rise Δp into a single dimensionless group, a p term.
3. The speed V of a weight when it hits the floor is assumed to depend on gravity g, the height h from where it was dropped, and the density r of the weight. Use dimensional analysis and write a relationship between the variables.
4. An object falls freely in a viscous fluid. Relate the terminal velocity V to its width w, its length l, gravity g, and the fluid density r and viscosity m. Select w, r, and m as repeating variables.
5. The pressure drop Δ p over a horizontal section of pipe of diameter d depends on the average velocity V, the viscosity m, the fluid density r, the average height e of the surface roughness elements, and the length L of the pipe section. Write an expression that relates the pressure drop to the other variables. Select d, V, and r as repeating variables.
6. The drag force F on a sphere depends on the sphere’s diameter d and
velocity V, the fluid’s viscosity m and density r, and gravity g. Write an expression for the drag force.
7. A model of a golf ball is to be studied to determine the effects of the dimples. A sphere 10 times larger than an actual golf ball is used in the wind tunnel study. What speed should be selected for the model to simulate a prototype speed of 50 m/s?
8. A towing force of 15 N is measured on a 1:40 scale model of a ship in a water channel. What velocity should be used to simulate a prototype speed of 10 m/s? What would be the predicted force on the ship at that speed?
9. A 1:20 scale model of an aircraft is studied in a 20°C supersonic wind tunnel at sea level. If a lift of 200 N at a speed of 250 m/s is measured in the wind tunnel, what velocity and lift does that simulate for the prototype? Assume the prototype is at 4000 m.
Labels: Fluid mechanics