 Figure 8.1 The details of a flow around a blunt body.
Figure 8.1 The details of a flow around a blunt body.The subject of external flows involves both low Reynolds-number flows and high Reynolds-number flows. Low Reynolds-number flows are not of interest in most engineering applications and will not be considered; flow around spray droplets, river sediment, filaments, and red blood cells would be examples that are left to the specialists. High Reynolds-number flows, however, are of interest to many engineers and include flow around airfoils, vehicles, buildings, bridge cables, stadiums, turbine blades, and signs, to name a few.
It is quite difficult to solve for the flow field external to a body, even the simplest of bodies like a long cylinder or a sphere. We can, however, develop equations that allow us to estimate the growth of the thin viscous layer, the boundary layer, which grows on a flat plate or the rounded nose of a vehicle. Also, coefficients have been determined experimentally that allow the drag and the lift to be approximated with sufficient accuracy.
The flow around a blunt body involves a separated region, a region in which the flow separates from the body and forms a recirculating region downstream, as

shown in Fig. 8.1. A wake, a region influenced by viscosity, is also formed; it is a diffusive region that continues to grow (some distance downstream the velocity is less than the free-stream velocity V ). A laminar boundary layer exists near the front of the body followed by a turbulent boundary layer as shown in Fig. 8.1. An inviscid flow, often referred to as the free stream, exists on the front of the body and outside the boundary layer, separated region, and wake. The flow around a streamlined body has all the same components as that of Fig. 8.1 except it does not have a significant separated region, and the wake is much smaller.
The free-stream inviscid flow is usually irrotational although it could be a rotational flow with vorticity, e.g., the flow of air near the ground around a tree trunk or water near the ground around a post in a river; the water digs a depression in the sand in front of the post and the air digs a similar depression in snow in front of the tree, a rather interesting observation. The vorticity in the approaching air or water accounts for the observed phenomenon.
It should be noted that the boundary of the separated region is shown at an aver- age location. It is, however, highly unsteady and is able to slowly exchange mass with the free stream, even though the time-average streamlines remain outside the separated region. Also, the separated region is always located inside the wake.
Interest in the flow around a blunt object is focused on the drag, the force the flow exerts on the body in the direction of the flow.1 Lift is the force exerted normal
to the flow direction and is of interest on airfoils and streamlined bodies. The and lift F are specified in terms of the drag coefficient C and lift coefficient C , respectively, by

The force due to the lower pressure in the separated region dominates the drag force on a blunt body, the subject of Sec. 8.2. The viscous stress that acts on and parallel to each boundary element is negligible and thus little, if any, attention is paid to the boundary layer on the surface of a blunt body. The opposite is true for an airfoil, the subject of Sec. 8.3; the drag force is primarily due to the viscous stresses that act on the boundary elements. Consequently, there is considerable interest in the boundary layer that develops on a streamlined body.
The basics of boundary-layer theory will be presented in Sec. 8.5. But first, the inviscid flow outside the boundary layer (see Fig. 8.1) must be known. So, inviscid flow theory will be presented in Sec. 8.4. The boundary layer is so thin that it can be ignored when solving for the inviscid flow. The inviscid flow solution provides the lift, which is not significantly influenced by the viscous boundary layer, and it also provides the pressure distribution on the body’s surface as well as the velocity on that surface (since the inviscid solution ignores the effects of viscosity, the fluid does not stick to the boundary but slips by the boundary). Both the pressure and the velocity at the surface are needed in the boundary-layer solution.
8.2 Flow Around Blunt Bodies
The primary flow parameter that influences the drag around a blunt body is the Reynolds number. If there is no free surface, the drag coefficients for both smooth and rough spheres and long cylinders are presented in Fig. 8.2; the values for streamlined cylinders and spheres are also included.
Separation always occurs in the flow of a fluid around a blunt body if the Reynolds number is sufficiently high. However, at low Reynolds numbers (it is
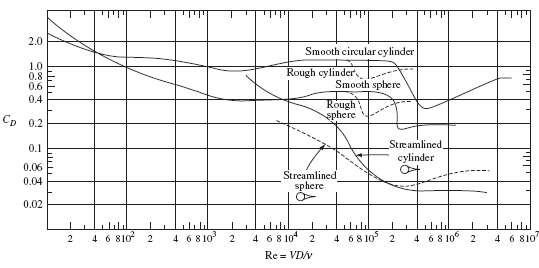
called a Stokes flow if Re < 5), there is no separation and the drag coefficient, for a sphere, is given by
Separation occurs for Re ≥ 10 beginning over a small area on the rear of the sphere until the separated region reaches a maximum at Re ≅ 1000. The drag coefficient is then relatively constant until a sudden drop occurs in the vicinity of Re = 2 × 105. This sudden drop is due to the transition of the boundary layer just before separation undergoing transition from a laminar flow to a turbulent flow. A turbulent boundary layer contains substantially more momentum and is able to move the separation region further to the rear (see the comparison in Fig. 8.3). The sudden decrease in drag could be as much as 80 percent. The surface of an object can be roughened to cause the boundary layer to undergo transition prematurely; the dimples on a golf ball accomplish this and increase the flight by up to 100 per- cent when compared to the flight of a smooth ball. After the sudden drop occurs, the drag coefficient again increases with increased Reynolds number. Experimental data does not provide the drag coefficients for either the sphere or the cylinder for high Reynolds numbers. The values of 0.4 for
Figure 8.3 Laminar and turbulent velocity profiles for the same boundary layer thickness.
long smooth cylinders and 0.2 for smooth spheres for Reynolds numbers exceeding 106 are often used (contrary to the data of Fig. 8.2).
Streamlining can substantially reduce the drag coefficients of blunt bodies. The drag coefficients for streamlined cylinders and spheres are also shown in Fig. 8.2. The included angle at the trailing edge should not exceed about 20° if the separated region is to be minimized. The drag due to the shear stress acting on the enlarged surface will certainly increase for a streamlined body, but the drag due to the low pressure will be reduced much more so that the total drag will be less. Also, stream- lining eliminates the vortices that cause vibrations when shed from a blunt body.
For cylinders of finite length with free ends, the drag coefficient must be reduced using the data of Table 8.1. If a finite-length cylinder has one end fixed to a solid
Table 8.1 Drag Coefficients for Finite-Length Circular Cylinders* with Free Ends†
| L/D | CD /C D∞ |
| ∞ | 1 |
| 40 | 0.82 |
| 20 | 0.76 |
| 10 | 0.68 |
| 5 | 0.62 |
| 3 | 0.62 |
| 2 | 0.57 |
| 1 | 0.53 |
surface, the length of the cylinder is doubled. Note that the L/D of a cylinder with free ends has to be quite large before the end effects are not significant.
Drag coefficients for a number of common shapes that are insensitive to high Reynolds numbers are presented in Table 8.2.
EXAMPLE 8.1
A 5-cm-diameter, 6-m-high pole fixed in concrete supports a flat, circular 4-m- diameter sign. For a wind speed of 30 m/s, estimate the maximum moment that must be resisted by the concrete.
Solution
To obtain the maximum moment, the wind is assumed normal to the sign. From Table 8.2 the drag coefficient for a disc is 1.1. The moment due to the drag force, which acts at the center of the sign, is
assuming a Reynolds number of Re = 30 × 0.05 / 1.5 × 10−5 = 10−5 and high- intensity fluctuations in the air flow, i.e., a rough cylinder. The factor from
Table 8.1 was not used since neither end was free. The moment that must be resisted by the concrete base is
M = M1 + M2 = 60 700 + 346 = 61 000 N ⋅ m
Long cylindrical bodies exposed to a fluid flow can exhibit the phenomenon of vortex shedding at relatively low Reynolds numbers. Vortices are shed from electrical wires, bridges, towers, and underwater communication wires, and can actually experience significant damage. We will consider the vortices shed from a long circular cylinder. The shedding occurs alternately from each side of the cylinder, as shown in Fig. 8.4. The shedding frequency f, in hertz, is given by the Strouhal number,
Figure 8.4 Vortices shed from a cylinder.
If this shedding frequency is the same, or a multiple of a structure’s frequency, then there is the possibility that damage may occur due to resonance.
The shedding frequency cannot be calculated from equations; it is determined experimentally and shown in Fig. 8.5. Note that vortex shedding initiates at Re ≈ 40 and for Re ≥ 300 the Strouhal number is essentially independent of Reynolds number and is equal to about 0.21. The vortex-shedding phenomenon disappears for Re > 104.
Figure 8.5 Strouhal number for vortex shedding from a cylinder.
EXAMPLE 8.2
A 6-cm-diameter cylinder is used to measure the velocity of a slow-moving air stream. Two pressure taps are used to determine that the vortices are shed with a frequency of 4 Hz. Determine the velocity of the air stream.
Solution
Assume the Strouhal number to be in the range 300 < Re < 10 000. Then
It is quite difficult to measure the velocity of an air stream this low. The measurement of the shed vortices is one method of doing so.
When a liquid flows from a region of relatively high pressure into a region of low pressure, cavitation may occur, that is, the pressure may be sufficiently low so that the liquid vaporizes. This can occur in pipe flows in which a contraction and expansion exists: in the vanes of a centrifugal pump, near the tips of propellers, on hydrofoils, and torpedoes. It can actually damage the propellers and the steel shafts (due to vibrations) on ships and cause a pump to cease to function properly. It can, however, also be useful in the destruction of kidney stones, in ultrasonic cleaning devices, and in improving the performance of torpedoes.
Cavitation occurs whenever the cavitation number s, defined by

where C (0) is given in Table 8.3 for several bodies for Re ≅ 105.
The hydrofoil, an airfoil-type shape that is used to lift a vessel above the water surface, invariably cannot operate without cavitation. The area and Reynolds number are based on the chord length. The drag and lift coefficients along with the critical cavitation numbers are presented in Table 8.4.
A 2-m-long hydrofoil with chord length of 40 cm operates at 30 cm below the water’s surface with an angle of attack of 6°. For a speed of 16 m/s determine the drag and lift and decide if cavitation exists on the hydrofoil.
Solution
The pressure p∞ must be absolute. It is
Assuming the water temperature is about 15°C, the vapor pressure is 1600 Pa (see Table C.1) so that the cavitation number is
This is less than the critical cavitation number of 1.2 given in Table 8.4 so cavitation is present. Note: we could have used p = 0, as is often done, with sufficient accuracy. The drag and lift are
8.3 Flow Around Airfoils
Airfoils are streamlined so that separation does not occur. Airfoils designed to oper- ate at subsonic speeds are rounded at the leading edge, whereas those designed for supersonic speeds may have sharp leading edges. The drag on an airfoil is primarily due to the shear stress that acts on the surface. The boundary layer, in which all the shear stresses are confined, that develops on an airfoil is very thin (see in Fig. 8.6) and can be ignored when solving for the inviscid flow surrounding the airfoil. The pressure distribution that is determined from the inviscid flow solution is influenced very little by the presence of the boundary layer. Consequently, the lift is estimated on an airfoil by ignoring the boundary layer and integrating the pressure distribution of the inviscid flow. The inviscid flow solution also provides the velocity at the outer edge of the thin boundary layer, a boundary condition needed when solving

the boundary-layer equations; the solution of the boundary-layer equations on a flat plate will be presented in Sec. 8.5.
The lift and drag on airfoils will not be calculated from the flow conditions but from graphical values of the lift and drag coefficients. These are displayed
in Fig. 8.7 for a conventional airfoil with Re ≅ 9 × 106. The lift and drag coefficients are defined as
Conventional airfoils are not symmetric and are designed to have positive lift at zero angle of attack, as shown in Fig. 8.7. The lift is directly proportional to the angle of attack until just before stall is encountered. The drag coefficient is also
directly proportional to the angle of attack up to about 5°. The cruise condition is at an angle of attack of about 2°, where the drag is a minimum at CL = 0.3 as noted.
Mainly, the wings supply the lift on an aircraft. But an effective length is the tip-to- tip distance, the wingspan, since the fuselage also supplies lift.
The drag coefficient is essentially constant up to a Mach number of about 0.75. It then increases by over a factor of 10 until a Mach number of one is reached at which point it begins to slowly decrease. So, cruise Mach numbers between 0.75 and 1.5 are avoided to stay away from the high drag coefficients. Swept-back airfoils are used since it is the normal component of velocity that is used when calculating the Mach number; that allows a higher plane velocity before the larger drag coefficients are encountered.

Slotted flaps are also used to provide larger lift coefficients during takeoff and landing. Air flows from the high-pressure region on the bottom of the airfoil through a slot to energize the slow-moving air in the boundary layer on the top side of the airfoil thereby reducing the tendency to separate and stall. The lift coefficient can reach 2.5 with a single-slotted flap and 3.2 with two slots.
EXAMPLE 8.4
Determine the takeoff speed for an aircraft that weighs 15 000 N including its cargo if its wingspan is 15 m with a 2-m chord. Assume an angle of attack of 8° at takeoff.
Solution
Assume a conventional airfoil and use the lift coefficient of Fig. 8.7 of about 0.95. The velocity is found from the equation for the lift coefficient:
The answer is rounded off to two significant digits, since the lift coefficient of is approximated from the figure.
Labels: Fluid mechanics