In fluid statics there is no relative motion between fluid particles so there are no shear stresses present (a shear results from a velocity gradient). This does not mean that the fluid particles are not moving, only that they are not moving relative to one another. If they are moving, as in a can of water rotating about its axis, they move as a solid body. The only stress involved in fluid statics is the normal stress, the pressure. It is the pressure acting over an area that gives rise to the force. Three types of problems are presented in this chapter: fluids at rest, as in the design of a dam; flu- ids undergoing linear acceleration, as in a rocket; and fluids that are rotating about an axis.
Pressure is a quantity that acts at a point. But, does it have the same magnitude in all directions at the point? To answer this question, consider Fig. 2.1. A pressure p is assumed to act on the hypotenuse and different pressures p and p on the other two sides of the infinitesimal element which has a uniform depth dz into the paper.
Figure 2.1 Pressure acting on an infinitesimal element.
The fluid particle occupying the fluid element could be accelerating so we apply Newton’s second law in both the x- and y-directions:
Here we see that the quantities on the right-hand sides of the equations are infinitesimal (multiplied by dx and dy), and can be neglected2 so that Since the angle b is arbitrary, this holds for all angles. We could have selected dimensions dx and dz and arrived at px = pz = p. So, in our applications to fluid statics, the pressure is a scalar function that acts equally in all directions at a point.
In the preceding discussion, pressure at a point was considered. But, how does pressure vary from point to point? The fluid element of depth dy in Fig. 2.2 is assumed to be accelerating. Newton’s second law provides
If the element were shown in the y-direction also, the y-component equation would be
Finally, the pressure differential can be written as
This can be integrated to give the desired difference in pressure between specified points in a fluid.
In a fluid at rest, there is no acceleration so the pressure variation from Eq. (2.8) is
If g is constant, Eq. (2.9) allows us to write
p = γ h 2.11)
where h = −Δz. Equation (2.11) is used to convert pressure to an equivalent height of a liquid; atmospheric pressure is often expressed as millimeters of mercury (the pressure at the bottom of a 30-in column of mercury is the same as the pressure at the earth’s surface due to the entire atmosphere).
If the pressure variation in the atmosphere is desired, Eq. (2.9) would be used with the ideal-gas law p = ρRT to give
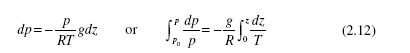
In the troposphere (between the earth’s surface and an elevation of about 10 km), the temperature in kelvins is T = 288 − 0.0065z; Eq. (2.12) can be integrated to give the pressure variation.
EXAMPLE 2.1
Convert 230 kPa to millimeters of mercury, inches of mercury, and feet of water.
Solution
Equation (2.11) is applied using the specific weight of mercury as 13.6γ water:
We could have converted meters of mercury to feet of mercury and then multi- plied by 13.6 to obtain feet of water.
A manometer is an instrument that uses a column of a liquid to measure pressure. A typical U-tube manometer containing mercury is attached to a water pipe, as shown in Fig. 2.3. There are several ways to analyze a manometer. One way is to identify two points that have the same pressure, i.e., they are at the same elevation in the same liquid, such as points 2 and 3. Then we write
Since point 4 is shown to be open to the atmosphere, p4 = 0. Thus, the manometer would measure the pressure p1 in the pipe to be
Figure 2.3 A U-tube manometer using water and mercury.
Some manometers will have several fluids with several interfaces. Each interface should be located with a point when analyzing a manometer.
EXAMPLE 2.2
A manometer connects an oil pipeline and a water pipeline, as shown. Determine the difference in pressure between the two pipelines using the readings on the manometer. Use Soil = 0.86 and SHg = 13.6.
The points of interest have been positioned on the manometer shown. The pres- sure at point 2 is equal to the pressure at point 3:
Observe that the heights must be in meters. The pressure at point 4 is essentially the same as that at point 5 since the specific weight of air is negligible compared to that of the oil. So,
Labels: Fluid mechanics
