When a liquid is contained by a surface, such as a dam, the side of a ship, a water tank, or a levee, it is necessary to calculate the force and its location due to the liquid. The liquid is most often water but it could be oil or some other liquid. We will develop equations for forces on plane surfaces, but forces on curved surfaces can be determined using the same equations. Examples will illustrate.
Consider the general surface shown in Fig. 2.4. The liquid acts on the plane area shown as a section of the wall; a view from the top gives additional detail of the geometry. The force on the plane surface is due to the pressure p = γh acting over the area, that is,
where y is the distance3 to the centroid of the plane area; the centroid is identified as the point C. Equation (2.16) can also be expressed as
Figure 2.4 The force on an inclined plane area.
Let’s assume that the force acts at some point called the center of pressure (c.p.), located by the point (x , y ). To determine where this point is, we must recognize that the sum of the moments of all the infinitesimal forces must equal the moment of the resultant force, that is,
where I is the moment of the area about its centroidal axis. So, substituting into Eq. (2.18) and using the expression for F from Eq. (2.16) results in
This allows us to locate where the force acts. For a horizontal surface, the pressure is uniform over the area so that the pressure force acts at the centroid of the area. In general, y is greater than y. The centroids and second moments of various areas are presented in books on statics or strength of materials. They will be given in the problems in this book.
If the top of the inclined area in Fig. 2.4 were at the free surface, the pressure distribution on that area would be triangular and the force F due to that pressure would act through the centroid of that triangular distribution, i.e., two-third the distance from the top of the inclined area. To locate the x-coordinate x of the center of pressure, we use
where I is the product of inertia of the area. Using the transfer theorem for the product of inertia, the x-location of the center of pressure is
Figure 2.5 Forces on a curved surface: (a) the gate, (b) the water and the gate, and (c) the gate only.
Often, the gate is composed of a quarter circle. In this case, the problem can be greatly simplified by recognizing that the forces F and F , when added together as a vector, must act through the center of the quarter circle since all the infinitesimal forces due to the water pressure on the gate that make up F and F act through the center. So, for a gate that has the form of a part of a circle, the force components F and F can be located at the center of the circular arc. An example will illustrate.
A final application of forces on surfaces involves buoyancy, i.e., forces on float- ing bodies. Archimedes’ principle states that there is a buoyancy force on a floating object equal to the weight of the displaced liquid, written as
FB = γ V displaced liquid (2.24)
Since there are only two forces acting on a floating body, they must be equal and opposite and act through the center of gravity of the body (the body could have density variations) and the centroid of the liquid volume. The body would position itself so the center of gravity of the body and centroid of the liquid volume would be on a vertical line. Questions of stability arise (does the body tend to tip?) but are not considered here.
EXAMPLE 2.3
A 60-cm square gate has its top edge 12 m below the water surface. It is on a 45° angle and its bottom edge is hinged as shown in (a). What force P is needed to just open the gate?
The first step is to sketch a free-body diagram of the gate so the forces and dis- tances are clearly identified. It is provided in (b). The force F is calculated to be
Consider the gate shown to be a quarter circle of radius 80 cm with the hinge 8 m below the water surface (see Fig. 2.5). If the gate is 1 m wide, what force P is needed to hold the gate in the position shown?
Solution
Let’s move the forces FH and FY to the center of the circular arc, as shown. This is allowed since all the infinitesimal force components that make up the resultant vector force FH + FV pass through the center of the arc. The forces that act on the gate are displayed. If moments are taken about the hinge, Fx , Fy , and FV produce no moments. So, there results
a rather simple result compared to the situation if we used Fig. 2.5c. The force P is
where FH = F1 , and F1 is the force on the vertical area shown in Fig. 2.5b.
2.2 Accelerating Containers
The pressure in a container accelerating with components a and a is found by integrating Eq. (2.8) between selected points 1 and 2 in Fig 2.6 to obtain
Figure 2.6 A linearly accelerating container.
If points 1 and 2 lie on a constant-pressure line (e.g., a free surface) such that p2 = p1, as in Fig. 2.6, and az = 0, Eq. (2.25) allows an expression for the angle a:
If a is not zero, it is simply included. The above equations allow us to make calculations involving linearly accelerating containers. The liquid is assumed to not be sloshing; it is moving as a rigid body. An example will illustrate. To determine the pressure in a rotating container, Eq. (2.8) cannot be used so it is necessary to derive the expression for the differential pressure. Refer to the infinitesimal element of Fig. 2.7. A top view of the element is shown. Newton’s second law applied in the radial r-direction provides, remembering that a = rΩ2
Expand the second term carefully, use sin dθ/2 = dθ/2, neglect higher order terms, and simplify Eq. (2.27) to
Figure 2.7 The rotating container and the top view of the infinitesimal element.
This provides the pressure variation in the radial direction and our usual dp = − rgdz provides the pressure variation in the z-direction. Holding z fixed, the pressure difference from r to r is found by integrating Eq. (2.28):.
If point 1 is at the center of rotation so that r1 = 0, then p2 = ρΩ r2 /2. If the distance from point 2 to the free surface (where p p2 = ρgh, we see that = 0) is h as shown in Fig. 2.8, so that
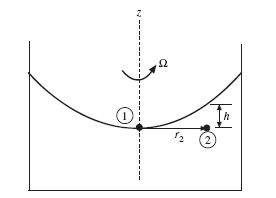
EXAMPLE 2.5
A 120-cm-long tank contains 80 cm of water and 20 cm of air maintained at 60 kPa above the water. The 60-cm-wide tank is accelerated at 10 m/s2. After equilibrium is established, find the force acting on the bottom of the tank.
Solution
First, sketch the tank using the information given in the problem statement. It appears as shown.
The distance x can be related to y by using Eq. (2.26):
EXAMPLE 2.6
The cylinder shown is rotated about the center axis. What rotational speed is required so that the water just touches point A? Also, find the force on the bottom of the cylinder for that speed.
The volume of the air before and after must be the same. Recognizing that the volume of a paraboloid of revolution is half of the volume of a circular cylinder of the same radius and height, the height of the paraboloid of revolution is found:
The pressure is integrated over the area to find the force to be
1. Two meters of water is equivalent to how many millimeters of mercury?
(A) 422 mm
(B) 375 mm
(C) 231 mm
(D) 147 mm
2. A U-tube manometer measures the pressure in an air pipe to be 10 cm of water. The pressure in the pipe is nearest
(A) 843 Pa
(B) 981 Pa
(C) 1270 Pa
(D) 1430 Pa
3. Calculate the pressure in the water pipe if h = 15 cm and H = 25 cm.
(A) 22.8 kPa
(B) 27.3 kPa
(C) 31.9 kPa
(D) 39.1 kPa
4. A submersible has a viewing window that is 60 cm in diameter. Determine the pressure force of the water on the window if the center of the window is 30 m below the surface and the horizontal window.
(A) 65.8 kN
(B) 79.3 kN
(C) 83.2 kN
(D) 99.1 kN
5. A 3-m-high, open cubical tank is filled with water. One end acts as a gate and has a hinge at the very bottom. What force at the very top of the gate is needed to just hold the gate shut?
(A) 44.1 kN
(B) 38.2 kN
(C) 23.9 kN
(D) 20.1 kN
6. The gate shown will open automatically when the water level reaches a certain height above the hinge. Determine that height if b is 1.6 m.
(A) 1.87m
(B) 2.12 m
(C) 2.77 m
(D) 2.91 m
7. A body weighs 200 N in air and 125 N when submerged in water. Its specific weight is nearest
(A) 2.31
(B) 2.49
(C) 2.54
(D) 2.67
8. A 1.4-m-high, 4.2-m-long enclosed tank is filled with water and accelerated horizontally at 6 m/s2. If the top of the tank has a small slit across the front, the maximum pressure in the tank is nearest
(A) 38.9 kPa
(B) 45.8 kPa
(C) 59.7 kPa
(D) 66.7 kPa
9. The force on the rear of the 80-cm-wide tank (the vertical end) of Prob. 8 is nearest
(A) 108 kN
(B) 95 kN
(C) 79 kN
(D) 56 kN
10. A test tube is placed in a rotating device that gradually positions the tube to a horizontal position. If the rate is 1000 rpm, estimate the pressure at the bottom of the relatively small-diameter test tube. The 12-cm-long tube contains water and the top of the tube is at a radius of 4 cm from the axis or rotation.
(A) 723 kPa
(B) 658 kPa
(C) 697 kPa
(D) 767 kPa
11. The U-tube is rotated about the right leg at 100 rpm. Calculate the pressures at A and B in the water if L is 40 cm.
(B) 7530 Pa, 2780 Pa
(C) 8770 Pa, 3920 Pa
(D) 9620 Pa, 2780 Pa
1. The specific gravity of a liquid is 0.75. What height of that liquid is needed to provide a pressure difference of 200 kPa?
2. Assume a pressure of 100 kPa absolute at ground level. What is the pressure difference between the top of a 3-m-high wall on the outside where the temperature is –20°C and on the inside of a house where the temperature is 22°C? (This difference results in infiltration even if no wind is present.)
3. The pressure at the nose of a small airplane is given by p = ρV 2 /2, where r is the density of air. A U-tube manometer measures 25 cm of water. Determine the airplane’s speed if it is flying at an altitude of 4000 m.
4. A submersible has a viewing window that is 60 cm in diameter. Determine the pressure force of the water on the window if the center of the window is 30 m below the surface and the window is at a 45° angle.
5. Find the force P needed to hold the 2-m-wide gate in the position shown if h = 1.2 m.
6. Find the force P needed to hold the 3-m-wide gate in the position shown if r = 2 m.
60 cm P
7.An object with a volume of 1200 cm3 weighs 20 N. What will it weigh when submerged in water?
8. A 1-m-high, 2-m-long enclosed tank is filled with water and accelerated horizontally at 6 m/s2. If the top of the tank has a small slit across the back, calculate the distance from the front of the tank on the bottom where the pressure is zero.
9. Estimate the force acting on the bottom of the 80-cm-wide tank of Prob. 8.
10. Find the pressure at point A in the cylinder if w = 100 rpm and R is 60 cm.
Labels: Fluid mechanics
