Internal Flows : Laminar Flow Between Rotating Cylinders ,Turbulent Flow in a Pipe and Open Channel Flow

7.1 Laminar Flow Between Rotating Cylinders

Steady flow between concentric cylinders, as shown in Fig. 7.6, is another example of a laminar flow that we can solve analytically. Such a flow exists below a Reynolds number5 of 1700. Above 1700, the flow might be a complex laminar flow or a turbulent flow. We will again solve this problem using a fluid element and using the appropriate Navier-Stokes equation; either method may be used.

THE ELEMENTAL APPROACH

Two rotating concentric cylinders are displayed in Fig. 7.6. We will assume vertical cylinders so body forces will act normal to the circular flow with the only nonzero velocity component vq. The element of fluid selected, shown in Fig. 7.6, has no angular

Figure 7.6 Flow between concentric cylinders.

acceleration in this steady-flow condition. Consequently, the summation of torques acting on the element is zero:

where t (r) is the shear stress and L is the length of the cylinders, which must be large when compared to the gap width d = r2 – r1. Equation (7.46) simplifies to

The last two terms of Eq. (7.46) are higher-order terms that are negligible when compared to the first two terms so that the simplified equation is

Now we must recognize that the t in Eq. (7.48) is6 −t of Table 5.1 with entry under“Stresses.” For this simplified application, the shear stress is related to the velocity gradient by

This allows Eq. (7.48) to be written, writing the partial derivatives as ordinary derivatives since vθ depends on r only, as

Multiply by dr, divide by mr, and integrate:

APPLYING THE NAVIER-STOKES EQUATIONS

The q-component differential momentum equation of Table 5.1 is selected for this circular motion with vr = 0 and vz = 0:

Replace the partial derivatives with ordinary derivatives since vθ depends on r

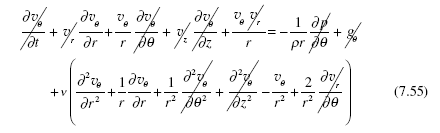
only and the equation becomes

QUANTITIES OF INTEREST

Many applications of rotating cylinders involve the outer cylinder being fixed, that is, ω2 = 0. The velocity distribution, found in the preceding two sections, with A and B simplified, becomes

This power, required because of the viscous effects in between the two cylinders, heats up the fluid in bearings and often demands cooling to control the temperature.

For a small gap between the cylinders, as occurs in lubrication problems, it is acceptable to approximate the velocity distribution as a linear profile, a Couette flow. Using the variable y of Fig. 7.6 the velocity distribution is

where y is measured from the outer cylinder in toward the center.

EXAMPLE 7.3

The viscosity is to be determined by rotating a 6-cm-diameter, 30-cm-long cylinder inside a 6.2-cm-diameter cylinder. The torque is measured to be 0.22 N · m and the rotational speed is measured to be 3000 rpm. Use Eqs. (7.61) and

(7.65) to estimate the viscosity. Assume that S = 0.86.

Solution

The torque is found from Eq. (7.63) based on the velocity distribution of Eq. (7.61):

We should check the Reynolds number to make sure the flow is laminar, as assumed. The Reynolds number is, using ν = μ /ρ,

ω r δ (3000 × 2π / 60) × 0.03 × 0.001

Re = 1 1 = = 619

ν 0.0131/(1000 × 0.86)

The laminar flow assumption is acceptable since Re < 1700.

7.5 Turbulent Flow in a Pipe

The Reynolds numbers for most flows of interest in conduits exceed those at which laminar flows cease to exist. If a flow starts from rest, it rather quickly undergoes transition to a turbulent flow. The objective of this section is to express the velocity distribution in a turbulent flow in a pipe and to determine quantities associated with such a flow.

A turbulent flow is a flow in which all three velocity components are nonzero and exhibit random behavior; in addition, there must be a correlation between the randomness of at least two of the velocity components. If there is no correlation, it is simply a fluctuating flow. For example, a turbulent boundary layer usually exists near the surface of an airfoil but the flow outside the boundary layer is not referred to as “turbulent” even though there are fluctuations in the flow; it is the free stream.

Let’s present one way of describing a turbulent flow. The three velocity components at some point are written as

where u denotes a time-average part of the x-component velocity and u′ denotes the fluctuating random part. The time-average of u is

where T is sufficiently large when compared to the fluctuation time. For a developed turbulent pipe flow, the three velocity components would appear as in Fig. 7.7. The only time-average component would be u in the flow direction. Yet there must exist a correlation between at least two of the random velocity fluctuations, e.g., u′v′ ≠ 0; such velocity correlations result in turbulent shear.

We can derive an equation that relates u′v′ and the time-average velocity component u in the flow direction of a turbulent flow but we cannot solve the equation

even for the simplest case of steady7 flow in a pipe. So, we will present experimental data for the velocity profile and define some quantities of interest for a turbulent flow in a pipe.

First, let us describe what we mean by a “smooth” wall. A “smooth” wall and a “rough” wall are shown in Fig. 7.8. The viscous wall layer is a thin layer near the pipe wall in which the viscous effects are significant. If this viscous layer of thickness dn

covers the wall roughness elements, the wall is “smooth,” as in Fig. 7.8a; if the rough-

ness elements protrude out from the viscous layer, the wall is “rough,” as in Fig. 7.8b.

There are two methods commonly used to describe the turbulent velocity profile in a pipe. These are presented in the following parts.

THE SEMI-LOG PROFILE

The time-average velocity profile in a pipe is presented for a smooth pipe as a semi- log plot in Fig. 7.9 with empirical relationships near the wall and centerline that

The interval 5 < uτ y/ν < 30 is a buffer zone in which the experimental data do not

fit either of the curves. The outer edge of the wall region may be as low as uτ y/ν =

3000 for a low Reynolds number flow.

The viscous wall layer plays no role for a rough pipe. The characteristic length is the average roughness height e and the wall region is represented by

The outer region is independent of the wall effects and thus is normalized for both smooth and rough walls using the radius as the characteristic length; it is

An additional empirical relationship h(y/r0 ) is needed to complete the profile for y > 0.15r . Most relationships that satisfy du /dy = 0 at y = r will do.

The wall region of Fig. 7.9a and the outer region of Fig. 7.9b overlap as displayed in Fig. 7.9a. For smooth and rough pipes, respectively,

We do not often desire the velocity at a particular location but, if we do, before umax can be found, uτ must be known. To find uτ we must know τ 0 . To find τ 0 we can use [see Eq. (7.5)]

The friction factor f can be estimated using the power-law profile that follows if the pressure drop is not known.

THE POWER-LAW PROFILE

Another approach, although not quite as accurate as the above, involves the power- law profile given by

Table 7.1 Exponent n for Smooth Pipes

Re = VD/n	4 × 103	105	106	>2 × 106
n	6	7	9	10

where n is between 5 and 10, usually an integer. This can be integrated to give the aver- age velocity:

For smooth pipes n is related to the Reynolds number in Table 7.1.

The power-law profile cannot be used to estimate the wall shear since it has an infinite slope at the wall for all values of n. It also does not have a zero slope at the pipe centerline so it is not valid near the centerline. It is, however, used to estimate the energy flux and momentum flux of pipe flows.

Finally, it should be noted that the kinetic-energy correction factor is 1.03 if n = 7;

hence, it is often taken as unity for turbulent flows.

EXAMPLE 7.4

Water at 20°C flows in a 4-cm-diameter pipe with a flow rate of 0.002 m3/s. Esti- mate (a) the wall shear stress, (b) the maximum velocity, (c) the pressure drop over 20 m, (d) the viscous layer thickness, and (e) determine if the wall is smooth or rough assuming the roughness elements to have a height of 0.0015 mm. Use the power-law profile.

Solution

First, the average velocity and Reynolds number are

The wall shear stress [see Eq. (7.74)] is

(e) The height of the roughness elements is given as 0.0015 mm (drawn tubing), which is less than the viscous layer thickness. Hence, the wall is smooth. Note: If the height of the wall elements was 0.046 mm (wrought iron), the wall would be rough.

LOSSES IN PIPE FLOW

The head loss is of considerable interest in pipe flows. It was presented in Eqs. (7.23) and (4.24) and is

So, once the friction factor is known, the head loss and pressure drop can be determined. The friction factor depends on a number of properties of the fluid and the pipe:

where the roughness height e accounts for the turbulence generated by the rough- ness elements. A dimensional analysis allows Eq. (7.79) to be written as

where e/D is termed the relative roughness.

Experimental data has been collected and presented in the form of the Moody diagram, displayed in Fig. 7.10 for developed flow in a pipe. The roughness heights are also included on the diagram. There are several features of this diagram that should be emphasized.

• A laminar flow exists up to Re ≅ 2000 after which there is a critical zone

in which the flow is undergoing transition to a turbulent flow. This may

involve transitory flow that alternates between laminar and turbulent flows.

• The friction factor in the transition zone, which begins at about Re = 4000

and decreases with increasing Reynolds numbers, becomes constant at the

end of the zone, as signified by the dashed line.

Figure 7.10 The Moody diagram.

• The friction factor in the completely turbulent zone is constant and depends on the relative roughness e/D. Viscous effects, and thus the Reynolds number, do not affect the friction factor.

• The height e of the roughness elements in the Moody diagram is for new pipes. Pipes become fouled with age changing both e and the diameter D resulting in an increased friction factor. Designs of piping systems should include such aging effects.

An alternate to using the Moody diagram is to use formulas developed by Swamee and Jain for pipe flow; the particular formula selected depends on the information given. The formulas to determine quantities in long reaches of developed pipe flow (these formulas are not used in short lengths or in pipes with numerous fittings and geometry changes) are as follows:

Either SI or English units can be used in the above equations. Note also that the Moody diagram and the above equations are accurate to within about 5 percent, sufficiently accurate for most engineering applications.

EXAMPLE 7.5

A pressure drop of 500 kPa is measured over 200 m of a horizontal length of 8-cm-diameter cast iron pipe transporting water at 20°C. Estimate the flow rate

using (a) the Moody diagram and (b) an alternate equation.

Solution

The relative roughness (find e in Fig. 7.10) is

Assuming a completely turbulent flow, the friction factor from Fig. 7.10 is f = 0.026. The head loss is

This equation was easier to use and gave an acceptable result.

LOSSES IN NONCIRCULAR CONDUITS

To determine the head loss in a relatively “open” noncircular conduit, we use the

hydraulic radius R, defined as

where A is the cross-sectional area and P is the wetted perimeter, the perimeter of the conduit that is in contact with the fluid. The Reynolds number, relative rough- ness, and head loss are, respectively,

A rectangular area should have an aspect ratio less than 4. This method should not be used with more complex shapes, like that of an annulus.

MINOR LOSSES

The preceding losses were for the developed flow in long conduits. Most piping systems, however, include sudden changes such as elbows, valves, inlets, etc., that add additional losses. These losses are called minor losses that may, in fact, add up to exceed the head loss found in the preceding sections. These minor losses are expressed in terms of a loss coefficient K, defined for most devices by

A number of loss coefficients are included in Table 7.2. Note that relatively low loss coefficients are associated with gradual contractions whereas relatively large coefficients with enlargements, due to the separated flows in enlargements. Separated and secondary flows also occur in elbows resulting in surprisingly large loss coefficients. Vanes that eliminate such separated or secondary flows can substantially reduce the losses, as noted in the table.

We often equate the losses in a device to an equivalent length of pipe, i.e.,

Table 7.2 Minor Loss Coefficients K for Selected Devices*

EXAMPLE 7.6

A 1.5-cm-diameter, 20-m-long plastic pipe transports water from a pressurized 400-kPa tank out to a free open end located 3 m above the water surface in the tank. There are three elbows in the water line and a square-edged inlet from the tank. Estimate the flow rate.

Solution

The energy equation is applied between the tank and the faucet exit:

Assume that the pipe has e/D = 0 and that Re ≅ 2 × 105 so that the Moody dia- gram gives f = 0.016. The energy equation gives

HYDRAULIC AND ENERGY GRADE LINES

The energy equation is most often written so that each term has dimensions of length, i.e.,

In piping systems it is often conventional to refer to the hydraulic grade line and the energy grade line. The hydraulic grade line (HGL), the dashed line in Fig. 7.11, is the locus of points located a distance p/g above the centerline of a pipe. The energy grade line (EGL), the solid line in Fig. 7.11, is the locus of points located a distance V 2 / 2 above the HGL. The following observations relate to the HGL and the EGL.

• The EGL approaches the HGL as the velocity goes to zero. They are identical on the surface of a reservoir.

• Both the EGL and the HGL slope downward in the direction of the flow due to the losses in the pipe.

• A sudden drop occurs in the EGL and the HGL equal to the loss due to a sudden geometry change, such as an entrance or a valve.

• A jump occurs in the EGL and the HGL due to a pump and a drop due to a turbine.

• If the HGL is below the pipe, there is a vacuum in the pipe, a condition that is most often avoided in piping systems because of possible contamination.

Figure 7.11 The hydraulic grade line (HGL) and the energy grade line (EGL).

7.6 Open Channel Flow

Consider the developed turbulent flow in an open channel, shown in Fig. 7.12. The water flows at a depth of y and the channel is on a slope S, which is assumed to be small so that sinθ = S. The cross section could be trapezoidal, as shown, or it could be circular or triangular. Let us apply the energy equation between the two sections:

where L is the distance between the two selected sections. Using the head loss expressed by Eq. (7.85), we have

The Reynolds number of the flow in an open channel is invariably large and the channel rough so that the friction factor is a constant independent of the velocity (see the Moody diagram of Fig. 7.10) for a particular channel. Consequently, the velocity is related to the slope and hydraulic radius by

Figure 7.12 Flow in an open channel.

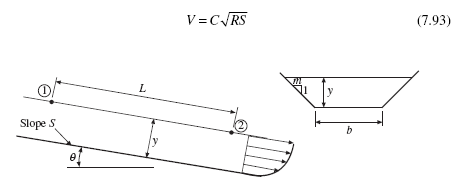
Table 7.3 Values* of the Manning n

Wall material	Manning n
Brick	0.016
Cast or wrought iron	0.015
Concrete pipe	0.015
Corrugated metal	0.025
Earth	0.022
Earth with stones and weeds	0.035
Finished concrete	0.012
Mountain streams	0.05
Planed wood	0.012
Sewer pipe	0.013
Riveted steel	0.017
Rubble	0.03
Unfinished concrete	0.014
Rough wood	0.013

where C is a dimensional constant called the Chezy coefficient; it has been related experimentally to the channel roughness and the hydraulic radius by

The dimensionless constant n is a measure of the wall roughness and is called the Manning n. Values for a variety of wall materials are listed in Table 7.3.

The flow rate in an open channel follows from Q = AV and is

This is referred to as the Chezy-Manning equation. It can be applied using English units by replacing the “1” in the numerator with “1.49.”

If the channel surface is smooth, e.g., glass or plastic, Eq. (7.95) should not be used since it assumes a rough surface. For channels with smooth surfaces the Darcy- Weisbach equation, Eq. (7.85), along with the Moody diagram should be used.

EXAMPLE 7.7

Water at 20°C is flowing in a 2-m-wide rectangular, brick channel at a depth of

120 cm. The slope is 0.0012. Estimate the flow rate using (a) the Chezy-Manning

equation and (b) the Darcy-Weisbach equation.

Solution

First, calculate the hydraulic radius:

(b) To use the Darcy-Weisbach equation, we must find the friction factor f. The Moody diagram requires a value for e. Use a relatively large value such as that  for rougher concrete, i.e., e = 2 mm. Since the hydraulic radius R = D/4 for a  circle, we use

Check the Reynolds number:

This is sufficiently large so that f is acceptable. Note that the Q of part (a) is about 12 percent lower than that of part (b). That of part (b) is considered more accurate.

Quiz No. 1

1. The maximum average velocity for a laminar flow of SAE-30 oil at 80°C in a 2-cm-diameter pipe using a critical Reynolds number of 2000 is nearest

(A) 1.8 m/s

(B) 1.4 m/s

(C) 1.0 m/s

(D) 0.82 m/s

2. Water is flowing in a 2-cm-diameter pipe with a flow rate of 0.0002 m3/s.

For a conventional entrance, estimate the entrance length if the water temperature is 40°C.

(A) 10 m

(B) 15 m

(C) 20 m

(D) 25 m

3. Water at 40°C flows through a 4-cm-diameter pipe at a rate of 6 L/min.

Assuming a laminar flow, the pressure drop over 20 m of length in the horizontal pipe is nearest

(A) 11 Pa

(B) 21 Pa

(C) 35 Pa

(D) 42 Pa

4. Water at 20°C flows through a 12-mm-diameter pipe on a downward slope so that Re = 2000. What angle would result in a zero pressure drop?

(A) 0.86°

(B) 0.48°

(C) 0.22°

(D) 0.15°

5. What pressure gradient dp/dx would provide a zero shear stress on the stationary lower plate for horizontal plates with the top plate moving to the right with velocity U. Assume a laminar flow with b separating the plates.

(A) U/b²

(B) 2U/b²

(C) 4U/b²

(D) U/2b²

6. Assuming a Couette flow between a stationary and a rotating cylinder, the power needed to rotate the inner rotating cylinder is

7. A 12-cm-diameter pipe transports water at 25°C in a pipe with roughness elements averaging 0.26 mm in height. Estimate the maximum velocity in the pipe if the flow rate is 0.0004 m3/s.

(A) 0.075 m/s

(B) 0.065 m/s

(C) 0.055 m/s

(D) 0.045 m/s

8. SAE-30 oil at 20°C is transported in a smooth 40-cm-diameter pipe with an average velocity of 10 m/s. Using the power-law velocity profile, estimate the pressure drop over 100 m of pipe.

(A) 300 kPa

(B) 275 kPa

(C) 250 kPa

(D) 225 kPa

9. Water at 20°C flows at 0.02 m3/s in an 8-cm-diameter galvanized-iron pipe.

Calculate the head loss over 40 m of horizontal pipe

(A) 6.9 m

(B) 8.1 m

(C) 9.7 m

(D) 10.3 m

10. If the pressure drop in a 100-m section of horizontal 10-cm-diameter galvanized-iron pipe is 200 kPa, estimate the flow rate if water at 20°C is flowing.

(A) 0.018 m3/s

(B) 0.027 m3/s

(C) 0.033 m3/s

(D) 0.041 m3/s

11. Water at 20°C flows from a reservoir out of a 100-m-long, 4-cm-diameter galvanized-iron pipe to the atmosphere. The outlet is 20 m below the surface of the reservoir. What is the exit velocity? There is a square-edged entrance.

(A) 2.0 m/s

(B) 3.0 m/s

(C) 4.0 m/s

(D) 5.0 m/s

12. Water flows in a 2-m-wide rectangular finished concrete channel with a slope of 0.001 at a depth of 80 cm. Estimate the flow rate.

(A) 2.15 m3/s

(B) 2.45 m3/s

(C) 2.75 m3/s

(D) 2.95 m3/s

Quiz No. 2

1. A drinking fountain has an opening of 4 mm in diameter. The water rises a distance of about 20 cm in the air. Is the flow laminar or turbulent as it leaves the opening? Make any assumptions needed.

2. SAE-30 oil at 80°C occupies the space between two cylinders of 2 cm and  2.2 cm in diameter. The outer cylinder is stationary and the inner cylinder rotates at 1000 rpm. Is the oil in a laminar or turbulent state? Use Re _crit = 1700 where Re = ωr₁ δ /ν  and δ = r₂– r₁ .

3. A parabolic velocity profile is desired at the end of a 10-m-long, 8-mm- diameter tube attached to a tank filled with water 20°C. An experiment is run during which 60 L is collected in 90 min. Is the laminar flow assumption reasonable?

4. The pressure drop over a 15-m length of 8-mm-diameter horizontal pipe transporting water at 40°C is measured to be 1200 Pa. A laminar flow is assumed. Determine the wall shear stress and the friction factor.

5. What pressure gradient is needed so that the flow rate is zero for laminar flow between horizontal parallel plates if the lower plate is stationary and the top plate moves with velocity U? The distance b separates the plates.

6. Water at 20°C flows down an 80-m-wide parking lot at a constant depth of 5 mm. The slope of the parking lot is 0.0002. Estimate the flow rate and the maximum shear stress.

7. SAE-10 oil at 20°C fills the gap between a rotating cylinder and a fixed outer cylinder. Estimate the torque needed to rotate a 20-cm-long cylinder at 40 rad/s assuming a Couette flow.

8. A 12-cm-diameter pipe transports water at 25°C in a pipe with roughness elements averaging 0.26 mm in height. Decide if the pipe is smooth or rough if the flow rate is 0.0004 m3/s.

9. SAE-30 oil at 20°C is transported in a smooth 40-cm-diameter pipe with an average velocity of 10 m/s. Using the power-law velocity profile, estimate the viscous wall layer thickness.

10. SAE-10 oil at 80°C flows at 0.02 m3/s in an 8-cm-diameter galvanized-iron pipe. Calculate the head loss over 40 m of horizontal pipe.

11. A pressure drop of 6000 Pa is measured over a 20 m length as water at 30°C flows through the 2- by 6-cm smooth conduit. Estimate the flow rate.

12. An 88 percent efficient pump is used to transport 30°C water from a lower reservoir through a 8-cm-diameter galvanized-iron pipe to a higher reservoir whose surface is 40 m above the surface of the lower one. The pipe has a total length of 200 m. Estimate the power required for a flow rate of 0.04 m3/s.

13.Water is not to exceed a depth of 120 cm in a 2-m-wide finished concrete channel on a slope of 0.001. What would the flow rate be at that depth?

Labels: Fluid mechanics