 Observe that this is essentially the same value found in Table C.1 for vg at 20°C.
Observe that this is essentially the same value found in Table C.1 for vg at 20°C.Thus far in our study of thermodynamics we have considered only single-component systems. In this chapter we will study the two-component system of air and water vapor, generally called psychrometrics. The more general presentation in which several components make up the system is not considered in this text. The two- component mixture of air and water vapor must be considered when designing air-conditioning systems, whether they are for heating, for cooling, or simply for dehumidification. A cooling tower used to remove heat from a power plant is an example of an air-conditioning system as is the usual heating and cooling system in an office building.
Air is a mixture of nitrogen, oxygen, and argon plus traces of some other gases. When water vapor is not included, we refer to it as dry air. If water vapor is included, as in atmospheric air, we must be careful to properly account for it. At the relatively low atmospheric temperature we can treat dry air as an ideal gas with constant
specific heats. It is also possible to treat the water vapor in the air as an ideal gas, even though the water vapor may be at the saturation state. Consequently, we can consider atmospheric air to be a mixture of two ideal gases.
Two models are used to study a mixture of ideal gases. The Amagat model treats each component as though it exists separately at the same pressure and temperature of the mixture; the total volume is the sum of the volumes of the components. In this chapter we use the Dalton model in which each component occupies the same volume and has the same temperature as the mixture; the total pressure is the sum of the component pressures, termed the partial pressures. For the Dalton model
P = Pa + Pv (8.1)
where the total pressure P is the sum of the partial pressure P of the dry air and the partial pressure P of the water vapor (called the vapor pressure). We will assume
the total pressure to be 100 kPa, unless stated otherwise.
To show that the water vapor in the atmosphere can be treated as an ideal gas, consider an atmosphere at 20°C. From Table C.1 at 20°C we see that P = 2.338 kPa, the pressure needed to vaporize water at 20°C. The ideal-gas law gives
Hence, we conclude that water vapor found in the atmosphere can be treated as an
ideal gas.
Since we assume that the water vapor is an ideal gas, its enthalpy is dependent on temperature only. Hence we use the enthalpy of the water vapor to be the enthalpy of saturated water vapor at the temperature of the air, expressed as
Figure 8.1 T-s diagram for the water vapor component.
This is acceptable for situations in which the total pressure is relatively low (near atmospheric pressure) and the temperature is below about 60°C.
The amount of water vapor in the air of state 1 in Fig. 8.1 is related to the relative humidity and the humidity ratio. The relative humidity f is defined as the ratio of the mass of the water vapor m to the maximum amount of water vapor m the air can hold at the same temperature:
where the constant-pressure lines for P and P are shown in Fig. 8.1.
The humidity ratio w (also referred to as specific humidity) is the ratio of the mass of water vapor to the mass of dry air:

When making an energy balance in an air-conditioning system we must use enthalpy, as with all control volumes involving gases. The total enthalpy is the sum of the enthalpy of the air and the enthalpy of the water vapor:
h = ha + ωhv (8.10)
where h is the specific enthalpy of the mixture per unit mass of dry air.
The temperature of the air as measured by a conventional thermometer is referred to as the dry-bulb temperature T (T1 in Fig. 8.1). The temperature at which condensation begins if air is cooled at constant pressure is the dew-point temperature Tdp (T3 in Fig. 8.1). If the temperature falls below the dew-point temperature, condensation occurs and the amount of water vapor in the air decreases. This may occur on a cool evening; it also may occur on the cool coils of an air conditioner, or the inside of a pane of glass when it’s cold outside, or on the outside of your glass filled with ice water sitting on a table.
EXAMPLE 8.1
The air at 25°C and 100 kPa in a 150-m3 room has a relative humidity of 60%. Calculate the humidity ratio, the dew point, the mass of water vapor in the air, and the volume percentage of the room that is water vapor using the equations in this section.
Solution
By Eq. (8.5), the partial pressure of the water vapor is

From the definition of the humidity ratio the mass of water vapor is found to be
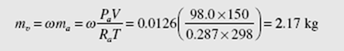
This demonstrates that air with 60% humidity is about 2% water vapor by volume. We usually ignore this when analyzing air and consider air to be dry air as we have done in the problems up to this point. Ignoring the water vapor does not lead to significant errors in most engineering applications. It must be included, however, when considering problems involving, for example, combustion and air-conditioning.
EXAMPLE 8.2
The air in Example 8.1 is cooled below the dew point to 10°C. Estimate the percentage of water vapor that will condense. Reheat the air to 25°C and calculate the relative humidity.
Solution
At 10°C the air is saturated, with f = 100%. In Fig. 8.1 we are at a state on the saturation line that lies below state 3. At l0°C we find from Table C.l that Pv = 1.228 kPa, so that
The difference in the humidity ratio just calculated and the humidity ratio of Example 8.1 is Δw = 0.0126 − 0.00773 = 0.00487 kg water/kg dry air. The mass of water vapor removed (condensed) is found to be
where P is used as the saturation pressure at 25°C interpolated in Table C.l.
It is quite difficult to measure the relative humidity f and the humidity ratio w directly, at least with any degree of accuracy. This section presents two indirect methods for accurately determining these quantities.
Consider a relatively long insulated channel, shown in Fig. 8.2; air with an unknown relative humidity enters, moisture is added to the air by the sufficiently long pool of water, and saturated air exits. This process involves no heat transfer because the channel is insulated and hence the exiting temperature is called the adiabatic saturation temperature. Let us find an expression for the desired humidity ratio wl. Consider that the liquid water added is at temperature T2. An energy balance on this control volume, neglecting kinetic and potential energy changes, is done considering the dry air and the water-vapor components. With Q = W = 0 we have
But, from conservation of mass for both the dry air and the water vapor,
where h – h = C (T − T ) for the dry air and h = h − h . Consequently, if we a2 al p 2 1 fg2 g2 f 2 measure the temperatures T and T and the total pressure P, we can find w2 from Eq. (8.15) and then w1 from Eq. (8.16) since the remaining quantities are given in App. C.
Because T is significantly less than T , the apparatus shown in Fig. 8.2 can be used to cool an air stream. This is done in relatively dry climates so that T is reduced but usually not to the saturation temperature. Such a device is often referred to as a “swamp cooler.” A fan blowing air through a series of wicks that stand in water is quite effective at cooling low-humidity air.
Using the device of Fig. 8.2 to obtain the adiabatic saturation temperature is a rather involved process. A much simpler approach is to wrap the bulb of a
thermometer with a cotton wick saturated with water, and then either to blow air over the wick or to swing the thermometer overhead through the air until the temperature reaches a steady-state value. This wet-bulb temperature T and the adiabatic saturation temperature are essentially the same for water if the pressure is approximately atmospheric.
EXAMPLE 8.3
The dry-bulb and wet-bulb temperatures of a 100-kPa air stream are measured to be 40 and 20°C, respectively. Determine the humidity ratio, the relative humidity, and the specific enthalpy of the air.
Solution
We use Eq. (8.16) to find w1. But first w2 is found using Eq. (8.15):
The specific enthalpy is found by assuming a zero value for air at T = 0°C (note that Tables C.1 and C.2 select h = 0 at T = 0°C so that establishes the datum).
Using Eq. (8.10) the enthalpy for the mixture is
h = ha + ωhv = CpT + ωhg = 1.0 × 40 + 0.00664 × 2574 = 57.1 kJ/kg dry air
where we have used h = hg at 40°C (see Fig. 8.1). The enthalpy is always expressed per mass unit of dry air.
Labels: Thermodynamics