A convenient way of relating the various properties associated with a water vapor-air mixture is to plot these quantities on a psychrometric chart, displayed in App. F, and shown in Fig. 8.3. Any two of the properties (T , φ, ω, Tdp , Twb ) establish a state from which the other properties are determined. As an example, consider a state A that islocated by specifying the dry-bulb temperature (T or, simply, T ) and the relative humidity. The wet-bulb temperature would be read at 1, the dew-point temperature at 2, the enthalpy at 3, and the humidity ratio at 4. Referring to App. F, a dry-bulb temperature of 30°C and a relative humidity of 80% would provide the following: Tdp = 26°C, Twb = 27°C, h = 85 kJ/(kg dry air), and w = 0.0215 kg water/(kg dry air). The chart provides us with a quick, relatively accurate method (large charts are used in the industry) for finding the quantities of interest. If the pressure is significantly different from 100 kPa, the equations presented in the preceding sections must be used.
EXAMPLE 8.4
Using App. F, rework Example 8.3 (T db= 40°C, Twb = 20°C) to find w, f, and h.
Solution
Using the chart, the intersection of T = 40°C and Twb = 20°C gives
These values are less accurate than those calculated in Example 8.3, but certainly are acceptable. The simplicity of using the psychrometric chart is obvious.
Figure 8.3 The psychrometric chart.
Generally, people feel most comfortable when the air is in the “comfort zone”: the temperature is between 22°C (72°F) and 27°C (80°F) and the relative humidity is between 40 and 60%. In Fig. 8.4, the area enclosed by the dotted lines represents the comfort zone. There are several situations in which air must be conditioned to put it in the comfort zone:
• The air is too cold or too hot. Heat is simply added or extracted. This is represented by A-C and B-C in Fig. 8.4.
• The air is too cold and the humidity is too low. The air can first be heated, and then moisture added, as in D-E-C.
• The temperature is acceptable but the humidity is too high. The air is first cooled from F to G. Moisture is removed from G to H. Heat is added from H to I.
• The air is too hot and the humidity is low. Moisture is added, and the process represented by J-K results. (This is a “swamp cooler.”) 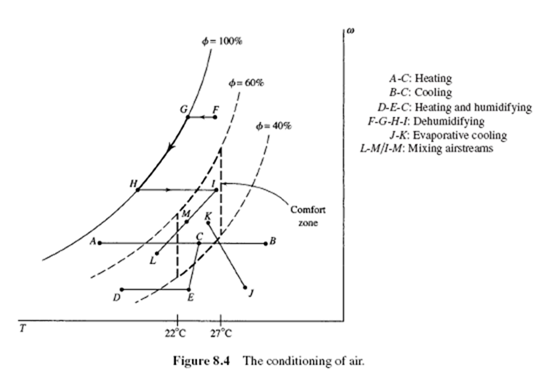
Several of these situations will be considered in the following examples. The first law will be used to predict the heating or cooling needed or to establish the final state.
Often the volume flow rate is used in air-conditioning problems; it is the average velocity in a conduit times the area of the conduit. It is customary to use the symbol Qf to represent the volume flow rate. Referring to Eq. (4.45), we observe that
The units on Q are m3/s. (The English units are often stated as cfs for ft3/sec or cfm
for ft3/min.)
EXAMPLE 8.5
Hot, dry air at 40°C and 10% relative humidity passes through an evaporative cooler. Water is added as the air passes through a series of wicks and the mixture exits at 27°C. Find the outlet relative humidity, the amount of water added, and the lowest temperature that could be realized.
Solution
The heat transfer is negligible in an evaporative cooler, so that h2 = h1. A constant enthalpy line is shown in Fig. 8.4 and is represented by J-K. At 27°C on the psychrometric chart we find that
The added water is found to be
The lowest possible temperature occurs when f = 100%: Tmin = 18.5°C.
EXAMPLE 8.6
Outside air at 5°C and 70% relative humidity is heated to 25°C. Calculate the rate of heat transfer needed if the incoming volume flow rate is 50 m3/min. Also, find the final relative humidity.
Solution
First, let’s find the mass flow rate of air. The density of dry air is found using the partial pressure Pin the ideal-gas law:
Using the psychrometric chart at state 1 (T = 5°C, f1 = 70%), we find h1 = 14 kJ/kg air. Since w remains constant (no moisture is added or removed), we follow curve A-C in Fig. 8.4; at state 2 we find that h = 35 kJ/kg air. Hence,
At state 2 we also note from the chart that f2 = 19%, a relatively low value.
EXAMPLE 8.7
Outside air at 5°C and 40% relative humidity is heated to 25°C and the final relative humidity is raised to 40% while the temperature remains constant by introducing steam at 400 kPa into the air stream. Find the needed rate of heat transfer if the incoming volume flow rate of air is 60 m3/min. Calculate the rate of steam supplied and the state of the steam introduced.
Solution
The process we must follow is first simple heating and then humidification, shown as D-E-C in Fig. 8.4. The partial pressure of dry air is
where we have assumed standard atmospheric pressure. The dry air density is
so that the mass flow rate of dry air is
The rate of heat addition is found using h and h from the psychrometric chart:
We assume that all the heating is done in the D-E process and that humidification takes place in a process in which the steam is mixed with the air flow. Assuming a constant temperature in the mixing process, conservation of mass demands that
where the air enters the humidifier at state 2 and leaves at state 3.
An energy balance around the humidifier provides hs m· s = (h3 − h2 )m· a . Hence,
This is less than h at 400 kPa. Consequently, the temperature of the steam is 144°C and the quality is
Only two significant figures are used because of inaccuracy using the relatively small psychrometric chart provided.
EXAMPLE 8.8
Outside air at 30°C and 90% relative humidity is conditioned so that it enters a building at 23°C and 40% relative humidity. Estimate the amount of moisture removed, the heat removed, and the necessary added heat.
Solution
The overall process is sketched as F-G-H-I in Fig. 8.4. Heat is removed during the F-H process, moisture is removed during the G-H process, and heat is added during the H-I process. Using the psychrometric chart, we find the moisture removed to be
Δω = ω3 − ω2 = 0.007 − 0.0245 = − 0.0175 kg water/kg dry air
where states 2 and 3 are at G and H, respectively. (The negative sign implies moisture removal.)
The heat that must be removed to cause the air to follow the F-G-H process is
qout = h3 − h1 = 26 − 93 = − 67 kJ/kg dry air
We neglected the small amount of heat due to the liquid state.
The heat that must be added to change the state of the air from the saturated state at H to the desired state at I is
qin = h4 − h3 = 41 − 26 = 15 kJ/kg dry air
If the air flow rate were given, the equipment could be sized.
EXAMPLE 8.9
Outside cool air at 15°C and 40% relative humidity (air stream 1) is mixed with inside air taken near the ceiling at 32°C and 70% relative humidity (air stream 2).
Determine the relative humidity and temperature of the resultant air stream 3 if
the outside flow rate is 40 m3/min and the inside flow rate is 20 m3/min.
Solution
An energy and mass balance of the mixing of air stream 1 with air stream 2 to produce air stream 3 would reveal the following facts relative to the psychrometric chart (see line L-M-I in Fig. 8.4):
• State 3 lies on a straight line connecting state 1 and state 2.
• The ratio of the distance 2-3 to the distance 3-1 is equal to m· a1 /m· a 2 . First, we determine m· a1 and m· a 2 :

where d2-3 is the distance from state 2 to state 3. State 3 is positioned on the psychrometric chart, and we find
Note: State 3 is located nearer state 1 since the greater outside flow dominates.
EXAMPLE 8.10
Water is used to remove the heat from the condenser of a power plant; 10 000 kg/min
of 40°C water enters a cooling tower, as shown. Water leaves at 25°C. Air enters at 20°C and leaves at 32°C. Estimate the volume flow rate of air into the cooling tower,
and the mass flow rate of water that leaves the cooling tower from the bottom.
Solution
An energy balance for the cooling tower provides
(Extrapolate to find h and w .) From the steam tables we use h at 40°C and find 2 2 f h3 = 167.5 kJ/kg and h4 = 104.9 kJ/kg. A mass balance on the water results in m· w 4 = m· w 3 − (ω2 − ω1 )m· a . Substituting this into the energy balance, with m· a1 = m· a 2 = m· a m results in
From the psychrometric chart we find that v1 = 0.84 m /kg dry air. This allows us
to find the volume flow rate:
This air flow rate requires fans, although there is some “chimney effect” since the hotter air tends to rise. Returning to the mass balance provides
If the exiting water is returned to the condenser, it must be augmented by 200 kg/min so that 10 000 kg/min is furnished. This is the makeup water.
1. Atmospheric air at 30°C and 100 kPa has a relative humidity of 40%.
Determine the humidity ratio using the equations (for accuracy).
| (A) | 10.1024 |
| (B) | 0.1074 |
| (C) | 0.1102 |
| (D) | 0.1163 |
2. The air in a 12 m × 15 m × 3 m room is at 20°C and 100 kPa, with a 50% relative humidity. Estimate the humidity ratio using the equations.
| (A) | 0.00716 |
| (B) | 0.00728 |
| (C) | 0.00736 |
| (D) | 0.00747 |
3. Using equations, estimate the mass of water vapor in the room of Prob. 2.
(A) 4.67 kg
(B) 4.93 kg
(C) 5.23 kg
(D) 5.81 kg
4. Using equations, estimate the total enthalpy (h = 0 at 0°C) in the room of
Prob. 2.
(A) 21 900 kJ
(B) 22 300 kJ
(C) 23 800 kJ
(D) 24 600 kJ
5. Outside air at 25°C has a relative humidity of 60%. Using the psychrometric
chart, the expected wet-bulb temperature is nearest
(A) 19.3°C
(B) 18.3°C
(C) 17.5°C
(D) 16.2°C
6. For which of the following situations would you expect condensation
to not occur?
(A) On a glass of ice water sitting on the kitchen table
(B) On the grass on a cool evening in Tucson, Arizona
(C) On your glasses when you come into a warm room on a cold winter day
(D) On the inside of a windowpane in an apartment that has high air infiltration on a cold winter day
7. The dry bulb temperature is 35°C and the wet-bulb temperature is 27°C.
What is the relative humidity?
(A) 65%
(B) 60%
(C) 55%
(D) 50%
8. The air in a conference room is to be conditioned from its present state of 18°C and 40% humidity. Select the appropriate conditioning strategy.
(A) Heat and dehumidify
(B) Cool, dehumidify, and then heat
(C) Heat, dehumidify, and then cool
(D) Heat and humidify
9. Air at 5°C and 80% humidity is heated to 25°C in an enclosed room. The
final humidity is nearest
(A) 36%
(B) 32%
(C) 26%
(D) 22%
10. Air at 35°C and 70% humidity in a 3 m × 10 m × 20 m classroom is cooled to 25°C and 40% humidity. How much water is removed?
(A) 4 kg
(B) 6 kg
(C) 11 kg
(D) 16 kg
11. A rigid 2-m3 tank contains air at 160°C and 400 kPa and a relative humidity of 20%. Heat is removed until the final temperature is 20°C. Determine the
temperature at which condensation begins.
(A) 101°C
(B) 109°C
(C) 116°C
(D) 123°C
12. The mass of water condensed during the cooling process in Prob. 11 is
nearest
(A) 4 kg
(B) 6 kg
(C) 11 kg
(D) 16 kg
13. The heat transfer necessary for the cooling of Prob. 11 to take place is nearest
(A) 5900 kJ
(B) 6300 kJ
(C) 6700 kJ
(D) 7100 kJ
14. Outside air at 10°C and 60% relative humidity mixes with 50 m3/min of inside air at 28°C and 40% relative humidity. If the outside flow rate is
30 m3/min, estimate the relative humidity using the psychrometric chart.
(A) 43%
(B) 46%
(C) 49%
(D) 52%
15. The mass flow rate of the exiting stream in Prob. 14 is nearest
(A) 94 kg/min
(B) 99 kg/min
(C) 110 kg/min
(D) 125 kg/min
1. Outside air at 30°C and 100 kPa is observed to have a dew point of 20°C. Find the relative humidity using equations (for accuracy).
(A) 53.8%
(B) 54.0%
(C) 54.4%
(D) 55.1%
2. Atmospheric air has a dry-bulb temperature of 30°C and a wet-bulb temperature of 20°C. Calculate the humidity ratio using the equations.
| (A) | 0.1054 |
| (B) | 0.1074 |
| (C) | 0.1092 |
| (D) | 0.1113 |
3. Using equations, estimate the relative humidity of the air in Prob. 2. (A) 40.2%
(B) 39.7%
(C) 39.5%
(D) 39.1%
4. Using equations, estimate the enthalpy per kg of dry air (h = 0 at 0°C) in
Prob. 2.
(A) 58.9 kJ/kg
(B) 58.1 kJ/kg
(C) 57.5 kJ/kg
(D) 57.0 kJ/kg
5. Atmospheric air at 10°C and 60% relative humidity is heated to 21°C. Use
the psychrometric chart to estimate the final humidity.
(A) 17%
(B) 20%
(C) 23%
(D) 26%
6. The rate of heat transfer needed in Prob. 5 if the mass flow rate of dry air is 50 kg/min is nearest
(A) 26 kJ/s
(B) 22 kJ/s
(C) 18 kJ/s
(D) 14 kJ/s
7. Which temperature is most different from the outside temperature as measured with a conventional thermometer?
(A) Wet-bulb temperature
(B) Dry-bulb temperature
(C) Dew-point temperature
(D) Ambient temperature
8. Estimate the liters of water in the air in a 3 m × 10 m × 20 m room if the temperature is 20°C and the humidity is 70%.
(A) 7.9 L
(B) 7.2 L
(C) 6.1 L
(D) 5.5 L
9. An evaporative cooler inlets air at 40°C and 20% humidity. If the exiting
air is at 80% humidity, the exiting temperature is nearest
(A) 30°C
(B) 28°C
(C) 25°C
(D) 22°C
10. Air at 30°C and 80% humidity is to be conditioned to 20°C and 40%
humidity. How much heating is required?
(A) 30 kJ/kg
(B) 25 kJ/kg
(C) 20 kJ/kg
(D) 15 kJ/kg
11. Outside air at 15°C and 40% humidity is mixed with inside air at 32°C and 70% humidity taken near the ceiling. Determine the relative humidity of the mixed stream if the outside flow rate is 40 m3/min and the inside flow rate is 20 m3/min.
(A) 64%
(B) 58%
(C) 53%
(C) 49%
12. The temperature of the mixed stream of Prob. 11 is nearest
(A) 28°C
(B) 25°C
(C) 23°C
(D) 20°C
13. One hundred m3/min of outside air at 36°C and 80% relative humidity is
conditioned for an office building by cooling and heating. Estimate the rate of cooling if the final state of the air is 25°C and 40% relative humidity.
(A) 9920 kJ/min
(B) 9130 kJ/min
(C) 8830 kJ/min
(D) 8560 kJ/min
14. The heating required to condition the air in Prob. 13 is nearest
(A) 1610 kJ/min
(B) 1930 kJ/min
(C) 2240 kJ/min
(D) 2870 kJ/min
Labels: Thermodynamics