A number of fluid properties must be used in our study of fluid mechanics. Density, mass per unit volume, was introduced in Eq. (1.7). We often use weight per unit volume, the specific weight g, related to density by
γ = ρg (1.11)
where g is the local gravity. For water g is taken as 9810 N/m3 unless otherwise stated. Specific weight for gases is seldom used.
Specific gravity S is the ratio of the density of a substance to the density of water and is often specified for a liquid. It may be used to determine either the density or the specific weight:
For example, the specific gravity of mercury is 13.6, which means that it is 13.6 times heavier than water. So, Pmercury = 13.6 × 1000 = 13 600 kg/m , where the density of water is 1000 kg/m3, the common value used for water.
Viscosity m can be considered to be the internal stickiness of a fluid. It results in shear stresses in a flow and accounts for losses in a pipe or the drag on a rocket. It can be related in a one-dimensional flow to the velocity through a shear stress by
where we call du/dr a velocity gradient; r is measured normal to a surface and u is tangential to the surface, as in Fig. 1.4. Consider the units on the quantities in Eq. (1.13): the stress (force divided by an area) has units of N/m2 so that the viscosity has the units N · s/m2.
To measure the viscosity, consider a long cylinder rotating inside a second cylinder, as shown in Fig. 1.4. In order to rotate the inner cylinder with the rotational
Figure 1.4 Fluid being sheared between two long cylinders.
speed Ω, a torque T must be applied. The velocity of the inner cylinder is RΩ and the velocity of the outer fixed cylinder is zero. The velocity distribution in the gap h between the cylinders is essentially a linear distribution as shown so that
![image_thumb[18] image_thumb[18]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhCdhnT0ZtkC9yr8uUyN3firc8sB4WQnllWylGrtP0Vo9NAPohXrzTI2g1_-utxO2iyKJmgxf8D42o-TYBddZhldx6MbWee_e3n-4l1zNmtfAB0_hNxnjOHXvoqnhX6Uf9TyAs7FqtJuZhN/?imgmax=800)
![image_thumb[19] image_thumb[19]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjiB2oEVGJqmen8i_eKZK21YEAD-HrALY3RWRng2YDYMhCHTcnPK4O-oWz-RvjOHwIi8vqVGXsZn9F_HGsGU7QcqzUb-dX4xA8K2z0Iha4rRrZIm6TnAHvXeIzRWIGpEQ1IMQmIczY0aEZW/?imgmax=800)
where the shear stresses acting on the ends of the long cylinder have been neglected. A device used to measure the viscosity is a viscometer.
In an introductory course, attention is focused on Newtonian fluids, those that exhibit a linear relationship between the shear stress and the velocity gradient, as in Eqs. (1.13) and (1.14) and displayed in Fig. 1.5 (the normal coordinate here is y). Many common fluids, such as air, water, and oil are Newtonian fluids. Non-Newtonian fluids are classified as dilatants, pseudoplastics, and ideal plastics and are also displayed.
A very important effect of viscosity is to cause the fluid to stick to a surface, the no-slip condition. If a surface is moving extremely fast, as a satellite entering the atmosphere, this no-slip condition results in very large shear stresses on the surface; this results in extreme heat which can incinerate an entering satellite. The no-slip
![image_thumb[20] image_thumb[20]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEglk5KxW2oB3NYjLbkjX1ZWV8DiH5EGJe5HdFKebpydDUPJuvDRsakfd2MBKUPmrA38JE1WaHYd9VPjYEgzXQO68D4j-DSXO9dWu1rS4H8LGAWewLoijF3bEvg9FhlaFbn0M9tvCyl93xNM/?imgmax=800)
condition also gives rise to wall shear in pipes resulting in pressure drops that require pumps spaced appropriately over the length of a pipe line transporting a fluid such as oil or gas.
Viscosity is very dependent on temperature. Note that in Fig. C.1, the viscosity of a liquid decreases with increased temperature, but the viscosity of a gas increases with increased temperature. In a liquid, the viscosity is due to cohesive forces, but in a gas, it is due to collisions of molecules; both of these phenomena are insensitive to pressure. So we note that viscosity depends on only temperature in both a liquid and a gas, i.e.,μ= μ(T).
The viscosity is often divided by density in equations so we have defined the kinematic viscosity to be
It has units of m2/s. In a gas, we note that kinematic viscosity does depend on pres- sure since density depends on both temperature and pressure.
The volume of a gas is known to depend on pressure and temperature. In a liquid, the volume also depends slightly on pressure. If that small volume change (or den- sity change) is important, we use the bulk modulus B, defined by

21 000 kPa is needed. So, it is obvious why we consider water to be incompressible. The bulk modulus is also used to determine the speed of sound c in water. It is given by
This yields about c = 1450 m/s for water at 20°C.
Another property of occasional interest in our study is surface tension s. It results from the attractive forces between molecules, and is included in Table C.1. It allows steel to float, droplets to form, and small droplets and bubbles to be spherical. Con- sider the free-body diagram of a spherical droplet and a bubble, as shown in Fig. 1.6. The pressure force inside the droplet balances the force due to surface tension around the circumference:
Figure 1.6 Free-body diagrams of (a) a droplet and (b) a bubble.
Notice that in a bubble there are two surfaces so that the force balance provides
So, if the internal pressure is desired, it is important to know if it is a droplet or a bubble.
A second application where surface tension causes an interesting result is in the rise of a liquid in a capillary tube. The free-body diagram of the water in the tube is shown in Fig. 1.7. Summing forces on the column of liquid gives

where the right-hand side of the equation is the weight W. This provides the height the liquid will climb in the tube:
The final property to be introduced in this section is vapor pressure. Molecules escape and reenter a liquid that is in contact with a gas, such as water in contact with air. The vapor pressure is that pressure at which there is equilibrium between the escaping and reentering molecules. If the pressure is below the vapor pressure, the molecules will escape the liquid; it is called boiling when water is heated to the temperature at which the vapor pressure equals the atmospheric pressure. If the local pressure is decreased to the vapor pressure, vaporization also occurs. This can happen when liquid flows through valves, elbows, or around turbine blades, should the pressure become sufficiently low; it is then called cavitation. The vapor pressure is found in Tables C.1 and C.5.
EXAMPLE 1.3
A 0.5 m × 2 m flat plate is towed at 5 m/s on a 2-mm-thick layer of SAE-30 oil at 38°C that separates it from a flat surface. The velocity distribution between the plate and the surface is assumed to be linear. What force is required if the plate and surface are horizontal?
Solution
The velocity gradient is calculated to be

Check the units to make sure the units of the force are newtons. The viscosity of the oil was found in Fig. C.1.
A machine creates small 1.0-mm-diameter bubbles of 20°C-water. Estimate the pressure that exists inside the bubbles.
Solution
Bubbles have two surfaces leading to the following estimate of the pressure:

A course in thermodynamics and/or physics usually precedes a fluid mechanics course. Those properties and relationships that are presented in those courses that are used in our study of fluids are included in this section. They are of particular use when compressible flows are studied, but they also find application to liquid flows.
We use the ideal-gas law in one of the two forms
where the pressure p and the temperature T must be absolute quantities. The gas constant R is found in Table C.4.
Enthalpy is defined as
where u is the specific internal energy (we use u since u is used for a velocity component). In an ideal gas we can use
where cp and cv are the specific heats also found in Table C.4. The specific heats are related to the gas constant by
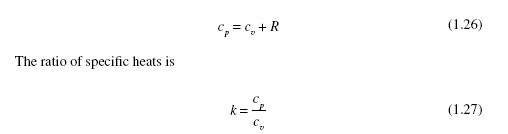
For adiabatic (no heat transfer) quasiequilibrium (properties are constant throughout the volume at an instant) processes the following relationships can be used for an ideal gas assuming constant specific heats:
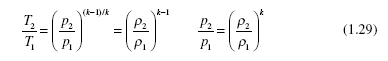
A small pressure wave with a relatively low frequency travels through a gas with a wave speed of
Finally, the first law of thermodynamics, which we will refer to simply as the energy equation, will be of use in our study; it states that when a system, a fixed set of fluid particles, undergoes a change of state from state 1 to state 2, its energy changes from E to E as it exchanges energy with the surroundings in the form of work W1-2 and heat transfer Q1-2. This is expressed as
To calculate the heat transfer from given temperatures and areas, a course on heat transfer is required, so it is typically a given quantity in thermodynamics and fluid
mechanics. The work, however, is a quantity that can often be calculated; it is a force times a distance and is often due to the pressure resulting in


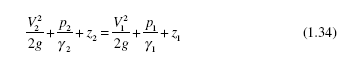 This equation does not follow directly from Eq. (1.31); it takes some effort to derive Eq. (1.34). An appropriate text could be consulted, but we will present it later in this book. It is presented here as part of our review of thermodynamics.
This equation does not follow directly from Eq. (1.31); it takes some effort to derive Eq. (1.34). An appropriate text could be consulted, but we will present it later in this book. It is presented here as part of our review of thermodynamics. EXAMPLE 1.5
A farmer applies nitrogen to a crop from a tank pressurized to 1000 kPa absolute at a temperature of 25°C. What minimum temperature can be expected in the
nitrogen if it is released to the atmosphere?
Solution
The minimum exiting temperature occurs for an isentropic process [see Eq. (1.29)]; it is
Such a low temperature can cause serious injury should a hose break and the nitrogen impact the farmer.
1. The correct units on viscosity are
(A) kg/(s · m)
(B) kg · m/s
(C) kg · s/m
(D) kg · m/s2
2. The mean free path of a gas is λ = 0.225m/(ρd 2 ) where d is the molecule’s diameter, m is its mass, and r the density of the gas. Calculate the mean free path of air at sea level. For an air molecule d = 3.7 × 10−10 m and m = 4.8 × 10−26 kg.
(A) 0.65×10−7 mm
(B) 6.5×10−7 m
(C) 65 nm
(D) 650 μm
3. A vacuum of 25 kPa is measured at a location where the elevation is 4000 m. The absolute pressure, in millimeters of mercury, is nearest
(A) 425 mm
(B) 375 mm
(C) 325 mm
(D) 275 mm
4. The equation is a good approximation to the pressure in the atmosphere. Estimate the pressure at 6000 m using this equation and calculate the percent error assuming p = 100 kPa and T0 = 15°C. (The more accurate value is found in Table C.3.)
(A) 4.4%
(B) 4.0%
(C) 3.2%
(D) 2.6%
5. A fluid mass of 1500 kg occupies 2 m3. Its specific gravity is nearest
(A) 1.5
(B) 0.75
(C) 0.30
(D) 0.15
6. A viscometer is composed of two 12-cm-long, concentric cylinders with radii 4 and 3.8 cm. The outer cylinder is stationary and the inner one rotates. If a torque of 0.046 N · m is measured on the inner cylinder at a rotational speed of 120 rpm, estimate the viscosity of the liquid. Neglect the contribution to the torque from the cylinder ends and assume a linear velocity profile.
(A) 0.127 N · s/m2
(B) 0.149 N · s/m2
(C) 0.161 N · s/m2
(D) 0.177 N · s/m2
7. A 0.1-m3 volume of water is observed to be 0.0982 m3 after a pressure is applied. What is that pressure?
(A) 37.8 MPa
(B) 24.2 MPa
(C) 11.7 MPa
(D) 8.62 MPa
8. The pressure inside a 20-μm-diameter bubble of 20°C water is nearest
(A) 17.8 kPa
(B) 24.2 kPa
(C) 29.4 kPa
(D) 38.2 kPa
9. A car with tires pressurized to 270 kPa (40 psi) leaves Phoenix with the tire temperature at 60°C. Estimate the tire pressure (gage) when the car arrives in Alaska with a tire temperature of –30°C.
(A) 270 kPa
(B) 210 kPa
(C) 190 kPa
(D) 170 kPa
10. Air at 22°C is received from the atmosphere into a 200 cm3 cylinder.
Estimate the pressure and temperature (MPa, °C) if it is compressed isentropically to 10 cm3.
| (A) | (6.53, 705) |
| (B) | (5.72, 978) |
| (C) | (4.38, 978) |
| (D) | (7.43, 705) |
11. Lightning is observed and thunder is heard 1.5 s later. About how far away did the lightning occur?
(A) 620 m
(B) 510 m
(C) 430 m
(D) 370 m
1. If force, length, and time are selected as the three fundamental dimensions, what are the dimensions on mass?
2. A pressure of 28 kPa is measured at an elevation of 2000 m. What is the absolute pressure in mm of Hg?
3. Water at 20°C flows in a 0.8-cm-diameter pipe with a velocity distribution of u(r) = 5[1 − (r 2 /16) × 106 ] m/s. Calculate the shear stress on the pipe wall.
4. SAE-30 oil at 30oC fills the gap between a 40-cm-diameter flat disk rotating
0.16 cm above a flat surface. Estimate the torque needed to rotate the disk at 600 rpm.
5. Water at 30°C is able to climb up a clean glass 0.2-mm-diameter tube due to surface tension. The water/glass angle is 0° with the vertical. How far up the tube does the water climb?
6. Derive an equation that relates the vertical force F needed to just lift a thin wire loop from a liquid assuming a vertical surface tension force. The wire radius is r and the loop diameter is D. Assume D >> r.
7. A 2-m-long, 4 cm-diameter shaft rotates inside an equally long
4.02-cm-diameter cylinder. If SAE-10W oil at 25°C fills the gap between the concentric cylinders, estimate the horsepower needed to rotate the shaft at 1200 rpm assuming a linear velocity profile.
8. The coefficient of thermal expansion aT allows the expansion of a liquid to be determined using the equation Δ V = αT V ΔT. What pressure is needed to cause the same decrease in volume of 2 m3 of 40°C water as that caused
by a 10°C drop in temperature?
9. Calculate the weight of the column of air contained above a 1-m2 area of atmospheric air from sea level to the top of the atmosphere.
10. Air expands from a tank maintained at 18°C and 250 kPa to the atmosphere. Estimate its minimum temperature as it exits.
Labels: Fluid mechanics