The Integral Equations : The Energy Equation and The Momentum Equation

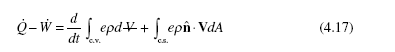
4.1 The Energy Equation

The first law of thermodynamics, or simply, the energy equation, is of use whenever heat transfer or work is desired. If there is essentially no heat transfer and no external work from a pump or some other device, the energy equation allows us to relate the pressure, the velocity, and the elevation. We will begin with the energy equation (4.8) in its general form:

Most applications allow a simplified energy equation by assuming a steady, uniform flow with one entrance and one exit, so that

where we have used nˆ ⋅ V = −V1 at the entrance. Using the continuity equation (4.14),

this is written as

The work rate term results from a force moving with a velocity: W = F ⋅ V. The force can be a pressure or a shear multiplied by an area. If the flow is in a conduit, e.g., a pipe or a channel, the walls do not move so there is no work done by the walls. If there is a moving belt, there could be an input of work due to the shear between the belt and the fluid. The most common work rate terms result from the pressure forces at the entrance and the exit (pressure is assumed to be uniform over each area) and from any device located between the entrance and the exit. The work rate term is expressed as

where power output is considered positive and W is the shaft power output from the control volume (a pump would provide a negative power and a turbine, a positive power output). Using the expression for e given in Eq. (1.33), Eq. (4.19) takes the form

The heat transfer term and the internal energy terms form the losses in the flow (viscous effects result in heat transfer and/or an increase in internal energy). Divide Eq. (4.21) by m g and simplify2:

where V is some characteristic velocity in the flow; if it is not obvious it will be specified. Some loss coefficients are listed in Table 7.2; in this chapter they will be given. The term h

is called the head loss because it has the dimension of length. We also refer to V 2/2g as the velocity head, p/g as the pressure head, and z as the head. The sum of these three terms is the total head.An incompressible flow occurs in many applications so that g1 = g2. Recall that g for water is 9810 N/m3.

The shaft-work term in Eq. (4.22) is typically due to either a pump or a turbine. If it is a pump, we can define the pump head H as

where W is the power output of the turbine and ηT is the turbine efficiency. Power has units of watts or horsepower.

If the flow is not uniform over the entrance and exit, an integration must be per- formed to obtain the kinetic energy. The rate at which the kinetic energy crosses an area is [see Eqs. (4.17) and (1.33)]

If the velocity distribution is known, the integration can be performed. A kinetic- energy correction factor a is defined as

so that, for nonuniform flows, the energy equation takes the form

where V 1 and V 2 are the average velocities at sections 1 and 2, respectively. Equation (4.30) is used if the values for a are known; for parabolic profiles, a = 2 in apipe and a = 1.5 between parallel plates. For turbulent flows (most flows in engineering applications), α ≅ 1.

EXAMPLE 4.3

Water flows from a reservoir with an elevation of 30 m through a 5-cm-diameter pipe that has a 2-cm-diameter nozzle attached to the end, as shown. The loss coefficient for the entire pipe is given as K = 1.2. Estimate the flow rate of water through the pipe. Also, predict the pressure just upstream of the nozzle (neglect the losses through the nozzle). The nozzle is at an elevation of 10 m.

Solution

The energy equation is written in the form

where the pressure is zero at surface 1 and at the exit 2, the velocity is zero at the surface, and there is no shaft work (there is no pump or turbine). The loss coefficient would be based on the characteristic velocity V in the pipe, not the exit velocity V . Use the continuity equation to relate the velocities:

The energy equation provides

The pressure just before the nozzle is found by applying the energy equation across the nozzle assuming no losses (Bernoulli’s equation could also be used):

EXAMPLE 4.4

An energy conscious couple decides to dam up the creek flowing next to their cabin and estimates that a head of 4 m can be established above the exit to a turbine they bought on eBay. The creek is estimated to have a flow rate of 0.8 m3/s. What is the maximum power output of the turbine assuming no losses and a velocity at the turbine’s exit of 3.6 m/s?

Solution

The energy equation is applied as follows:

It is only the head of the water above the turbine that provides the power; the exiting velocity subtracts from the power. There results, using m = ρQ = 1000 × 0.8 = 800 kg/s,

4.4 The Momentum Equation

When a force is involved in a calculation, it is often necessary to apply Newton’s second law, or simply, the momentum equation, to the problem of interest. For some general volume, using the Eulerian description of motion, the momentum equation was presented in Eq. (4.10) in its most general form for a fixed control volume as

When applying this equation to a control volume, we must be careful to include all forces acting on the control volume, so it is very important to sketch the control volume and place the forces on the sketch. The control volume takes the place of the free-body diagram utilized in mechanics courses.

Most often, steady, uniform flows with one entrance and one outlet are encountered. For such flows, Eq. (4.31) reduces to

Using continuity the momentum equation takes the simplified form

This is the form most often used when a force is involved in a calculation. It is a vector equation that contains the following three scalar equations (using rectangular coordinates):

If the profiles at the entrance and exit are not uniform, Eq. (4.31) must be used and the integration performed or, if the momentum-correction factor b is known, it can be used. It is found from

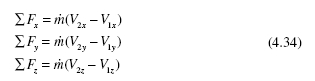
The momentum equation for a steady flow with one entrance and one outlet then takes the form

where V₁and V₂ represent the average velocity vectors over the two areas. For parabolic profiles, b = 1.33 for a pipe and b = 1.2 for parallel plates. For turbulent flows (most flows in engineering applications), b ≅ 1.

One of the more important applications of the momentum equation is on the deflectors (or vanes) of pumps, turbines, or compressors. The applications involve both stationary deflectors and moving deflectors. The following assumptions are made for both:

• The frictional force between the fluid and the deflector is negligible.

• The pressure is constant as the fluid moves over the deflector.

• The body force is assumed to be negligible.

• The effect of the lateral spreading of the fluid stream is neglected.

A sketch is made of a stationary deflector in Fig. 4.3. Bernoulli’s equation predicts that the fluid velocity will not change ( V2 = V1 ) as the fluid moves over the deflector.

Figure 4.3 A stationary deflector.

Figure 4.4 A single moving deflector.

Since the pressure does not change, there is no friction, it is a steady flow, and the body forces are neglected. The component momentum equations appear as follows:

Given the necessary information, the force components can be calculated. The analysis of a moving deflector is more complicated. Is it a single deflector (a water scoop to slow a high-speed train), or is it a series of deflectors as in a turbine? First, let us consider a single deflector moving with speed V , as shown in Fig. 4.4. The reference frame is attached to the deflector so the flow is steady from such a reference frame3. The deflector sees the velocity of the approaching fluid as the relative velocity V and it is this relative velocity that Bernoulli’s equation predicts will remain constant over the deflector, i.e., V = V . The velocity of the fluid exiting the fixed nozzle is V . The momentum equation then provides

3If the deflector is observed from the fixed jet, the deflector moves away from the jet and the flow is not a steady flow. It is steady if the flow is observed from the deflector.

Figure 4.5 A series of vanes.

where m r is that part of the exiting fluid that has its momentum changed. As the deflector moves away from the nozzle, the fluid represented by the length VB Δt does not experience a change in momentum. The mass flux of fluid that experiences a momentum change is

which provides us with the relative mass flux used in the expressions for the force components.

For a series of vanes, the nozzles are typically oriented such that the fluid enters the vanes from the side at an angle b1 and leaves the vanes at an angle b2, as shown in Fig. 4.5. The vanes are designed so that the relative inlet velocity V enters the vanes tangent to a vane (the relative velocity always leaves tangent to the vane) as shown in Fig. 4.6. It is the relative speed that remains constant in magnitude as the fluid moves over the vane, i.e., V

= V . We also note that all of the fluid exiting the fixed jet has its momentum changed. So, the expression to determine the x-component of the force is

Figure 4.6 (a) Average position of the jet, (b) the entrance velocity polygon, and (c) the exit velocity polygon.

It is this x-component of the force that allows the power to be calculated; the y-component does no work and hence does not contribute to the power. The power is found fromwhere N is the number of jets in the device and we have observed that the force R  moves with velocity V_B .

EXAMPLE 4.5

A 10-cm-diameter hose maintained at a pressure of 1600 kPa provides water from a tanker to a fire. There is a nozzle on the end of the hose that reduces the diameter to 2.5 cm. Estimate the force that the water exerts on the nozzle. The losses can be neglected in a short nozzle.

Solution

A sketch of the water contained in the nozzle is important so that the control volume is carefully identified. It is shown. Note that p2 = 0 and we expect

that the force F of the nozzle on the water acts to the left. The velocities are needed upstream and at the exit of the nozzle. Continuity provides

EXAMPLE 4.6

A steam turbine contains eight 4-cm-diameter nozzles each accelerating steam to 200 m/s, as shown. The turbine blades are moving at 80 m/s and the density of the steam is 2.2 kg/m3. Calculate the maximum power output.

Solution

The angle a1 is determined from the velocity polygon of Fig. 4.6b. For the x- and y-components, using V = 200 m/s and V B = 80 m/s, we have

There are two unknowns in the above two equations: Vr₁ and α₁. A simultaneous solution provides

Neglecting losses allows Vr ₂ = Vr₁ = 136.7 m/s so the velocity polygon at the exit (see Fig.4.6c) provides

EXAMPLE 4.7

The relatively rapid flow of water in a horizontal rectangular channel can sud- denly “jump” to a higher level (an obstruction downstream may be the cause). This is called a hydraulic jump. For the situation shown, calculate the higher depth downstream. Assume uniform flow.

This equation is a cubic but with a little ingenuity it’s a quadratic. Let’s factor:

This rather interesting effect is analogous to the shock wave that occurs in a supersonic gas flow. It is nature’s way of moving from something traveling quite fast to something moving relatively slow while maintaining continuity and momentum. The energy that is lost when making this sudden change through the hydraulic jump can be found by using the energy equation.

Quiz No. 1

1. The time derivative can be moved inside the volume integral in the system- to-control-volume transformation because

(A) The integrand is time independent

(B) The limits of integration are time independent

(C) The integral is over space coordinates

(D) The volume is allowed to deform

2. Air at 25°C and 240 kPa flows in a 10-cm-diameter pipe at 40 m/s. The mass flux is nearest

(A) 0.94 kg/s

(B) 1.14 kg/s

(C) 1.25 kg/s

(D) 1.67 kg/s

3. Water flows in a 2- by 4-cm rectangular duct at 16 m/s. The duct undergoes a transition to a 6-cm-diameter pipe. Calculate the velocity in the pipe.

(A) 2.76 m/s

(B) 3.14 m/s

(C) 3.95 m/s

(D) 4.53 m/s

4. A balloon is being filled with water at an instant when the diameter is 50 cm.

If the flow rate into the balloon is 0.01 m3/s, the rate of increase in the diameter is nearest

(A) 2.1 cm/s

(B) 2.6 cm/s

(C) 3.2 cm/s

(D) 3.8 cm/s

5. A sponge is contained in a volume that has one 4-cm-diameter inlet A into mwhich water flows and two 2-cm-diameter outlets, A and A . The sponge is to have dm/dt = 0. Find V1 if Q2 = 0.002 m /s and m· 3 = 2.5 kg/s.

(A) 3.58 m/s

(B) 3.94 m/s

(C) 4.95 m/s

(D) 5.53 m/s

6. The energy equation does not assume which of the following

(A) Steady flow

(B) Incompressible flow

(C) Uniform flow

(D) Viscous effects

7. Water enters a horizontal nozzle with diameter d1 = 8 cm at 10 m/s and exits to the atmosphere through a 4-cm-diameter outlet. The pressure upstream of the nozzle is nearest

(A) 600 kPa

(B) 650 kPa

(C) 700 kPa

(D) 750 kPa

8. Water is transported from one reservoir with surface elevation of 135 m to a lower reservoir with surface elevation of 25 m through a 24-cm-diameter pipe. Estimate the flow rate through the pipe if the loss coefficient between the two surfaces is 20.

(A) 0.23 m3/s

(B) 0.34 m3/s

(C) 0.47 m3/s

(D) 0.52 m3/s

9. A turbine extracts energy from water flowing through a 10-cm-diameter pipe at a pressure of 800 kPa with an average velocity of 10 m/s. If the turbine is 90 percent efficient, how much energy can be produced if the water is emitted from the turbine to the atmosphere through a 20-cm- diameter pipe?

(A) 65 kW

(B) 70 kW

(C) 75 kW

(D) 80 kW

10. A 10-cm-diameter hose delivers 0.04 m3/s of water through a 4-cm- diameter nozzle. The force of the water on the nozzle is nearest

(A) 1065 N

(B) 1370 N

(C) 1975 N

(D) 2780 N

11. A hydraulic jump (a sudden jump for no apparent reason) can occur in a rectangular channel with no apparent cause. The momentum equation allows the height downstream to be calculated if the upstream height and velocity are known. Neglect any frictional force on the bottom and sidewalls and determine y2 in the rectangular channel if V1 = 10 m/s and y1 = 50 cm.

(A) 2.75 m

(B) 2.95 m

(C) 3.15 m

(D) 3.35 m

12. A 6-cm-diameter horizontal stationary water jet having a velocity of 40 m/s strikes a vertical plate. The force needed to hold the plate if it moves away from the jet at 20 m/s is nearest

(A) 1365 N

(B) 1270 N

(C) 1130 N

(D) 1080 N

13.The blades of Fig. 4.5 deflect a jet of water having V = 40 m/s. Determine

the required blade angle a ₁ if b₁ = 30°, a₂ = 45°, and V_B = 20 m/s. (A) 53.8°

(B) 56.4°

(C) 58.2°

(D) 63.4°

14. If the jet in Prob. 13 is 2 cm in diameter, estimate the force of the jet on the blade.

(A) 387 N

(B) 404 N

(C) 487 N

(D) 521 N

Quiz No. 2

1. Water flows in a 2- by 4-cm rectangular duct at 16 m/s. The duct undergoes a transition to a 6-cm-diameter pipe. Calculate the velocity in the pipe.

2. Air flows in a 20-cm-diameter duct at 120°C and 120 kPa with a mass flux of 5 kg/s. The circular duct converts to a 20-cm square duct in which the temperature and pressure are 140°C and 140 kPa, respectively. Determine the velocity in the square duct.

3. Air at 40°C and 250 kPa is flowing in a 32-cm-diameter pipe at 10 m/s. The pipe changes diameter to 20 cm and the density of the air changes to 3.5 kg/m3. Calculate the velocity in the smaller diameter pipe.

4. Atmospheric air flows over the flat plate as shown. Viscosity makes the air stick to the surface creating a thin boundary layer. Estimate the mass flux m· of the air across the surface that is 10 cm above the 120-cm-wide plate if u(y) = 800 y.

5. A sponge is contained in a volume that has one 4-cm-diameter inlet A into which water flows and two outlets, A and A . Determine dm/dt of the sponge if V = 5 m/s, Q2 = 0.002 m3/s, and m· = 2.5 kg/s.

6. Water flows from a reservoir with an elevation of 25 m out to a 12-cm- diameter pipe that has a 4-cm-diameter nozzle attached to the end. The loss coefficient for the entire pipe is given as K = 2. Estimate the flow rate of water through the pipe. The nozzle is at an elevation of 10 m.

7. A dam is proposed on a remote stream that measures approximately 25-cm deep by 350-cm wide with an average velocity of 2.2 m/s. If the dam can be constructed so that the free surface above a turbine is 10 m, estimate the maximum power output of an 88 percent efficient turbine.

8. An 85 percent efficient pump is used to increase the pressure in water from 120 to 800 kPa in a 10-cm-diameter pipe. What is the required horsepower of the pump for a flow rate of 20 L/s?

9. Air enters a compressor at 25°C and 10 kPa with negligible velocity. It exits through a 2-cm-diameter pipe at 400 kPa and 160°C with a velocity of 200 m/s. Determine the heat transfer if the power required is 18 kW.

10. A turbine is located in a 24-cm-diameter pipe. A piezometer tube upstream of a turbine measures the same pressure as a pitot tube downstream of the turbine. If the upstream velocity is 20 m/s and the turbine is 90 percent efficient, what is the turbine output?

11. A nozzle with exit diameter d is attached to a hose of diameter 3d with upstream pressure of 200 kPa. The nozzle changes the direction of the water flow from the hose through an angle of 90°. Calculate the magnitude of the force of the water on the nozzle if d = 1 cm.

12. A hydraulic jump (a sudden jump for no apparent reason) can occur in a rectangular channel with no apparent cause. The continuity and momentum equations allow the variables to be related. Neglect any frictional force on the bottom and sidewalls and determine V1 in the rectangular channel if V2 = V1/4.

13. A 4-cm-diameter horizontal stationary water jet having a velocity of 50 m/s strikes a cone having an included angle at the apex of 60°. The water leaves the cone symmetrically. Determine the force needed to hold the cone if it moves into the jet at 20 m/s.

14. The blades of Fig. 4.6 deflect a 2-cm-diameter jet of water having V1 = 40 m/s. Determine the blade angle a1 and the power produced by the jet assuming no losses if b1 = 20°, a2 = 50°, and VB = 15 m/s.

Labels: Fluid mechanics