where λp and λs are the pass-band edge and stop-band edge, respectively.Here, we summarize three basic types of analog low-pass filters that can be used as prototype for designing IIR filters. For each type, we give the transfer function, its magnitude response, and the order N needed to satisfy the (analog) specification. We use Ha (s ) to denote the transfer function of an analog filter, where s is the complex variable in the Laplace transform. Each of these filters have all its poles on the left- half s plane, so that it is stable. We use the variable λ to represent the analog frequency in radians/second. The frequency response Ha (λ) is the transfer function evaluated at s = j λ.
The analog low-pass filter specification, as shown in Fig. 12.12, is given by
The transfer function of an Nth-order Butterworth filter is given by
order required to satisfy Eq. (12.8) is
For inverse Chebyshev filters, the equiripples are inside the stop band, as opposed to the pass band in the case of Chebyshev filters. The magnitude response square of the inverse Chebyshev filter is
when N is odd. The filter order N required to satisfy Eq. (12.8) is the same as that for the Chebyshev filter, which is given by Eq. (12.17).
In comparison, the Butterworth filter requires a higher order than both types of Chebyshev filters to satisfy the same specification. There is another type of filters called elliptic filters (Cauer filters) that have equiripples in the pass band as well as in the stop band. Because of the lengthy expressions, this type of filters is not given here (see the references). The Butterworth filter and the inverse Chebyshev filter have better (closer to linear) phase characteristics in the pass band than Chebyshev and elliptic filters. Elliptic filters require a smaller order than Chebyshev filters to satisfy the same specification.
Design Using Bilinear Transformations
One of the most simple ways of designing a digital filter is by way of transforming an analog low-pass filter to the desired digital filter. Starting from the desired digital filter specification, the low-pass analog specification is obtained. Then, an analog low-pass filter Ha (s ) is designed to meet the specification. Finally, the desired digital filter is obtained by transforming Ha (s ) to H(z). There are several types of transformation. The all-around best one is the bilinear transformation, which is the subject of this subsection.
In a bilinear transformation, the variable s in Ha (s ) is replaced with a bilinear function of z to obtain H(z). Bilinear transformations for the four standard types of filters, namely, low-pass filter (LPF), high- pass filter (HPF), bandpass filter (BPF), and bandstop filter (BSF), are shown in Table 12.1. The second column in the table gives the relations between the variables s and z. The value of T can be chosen arbitrarily without affecting the resulting design. The third column shows the relations between the analog frequency λ and the digital frequency f , obtained from the relations between s and z by replacing s with j λ and z with exp( j 2π f ). The fourth and fifth columns show the required pass-band and stop-band edges for the analog LPF. Note that the allowable variations in the pass band and stop band, or equivalently the values of ε and δ, for the analog low-pass filter remain the same as those for the desired digital filter. Notice that for the BPF and BSF, the transformation is performed in two steps: one for transforming an analog LPF to/from an analog BPF (or BSF), and the other for transforming an analog BPF (or BSF) to/from a
digital BPF (or BSF). The values of W and λ˜0 are chosen by the designer. Some convenient choices are: (1) W = λ˜ p2 − λ˜ p1 and λ˜2 = λ˜ p1λ˜ p2, which yield λp = 1; (2) W = λ˜s 2 − λ˜s 1 and λ˜2 = λ˜s 1λ˜s 2, which yield λs = 1. We demonstrate the design process by the following two examples.
Design Example 1
Consider designing a digital LPF with a pass-band edge at f p = 0.15 and stop-band edge at fs = 0.25. The magnitude response in the pass band is to stay within 0 and−2 dB, although it must be no larger than −40 dB in the stop band. Assuming that the analog Butterworth filter is to be used as the prototype filter, we proceed the design as follows.
Design Example 2
Now, suppose that we wish to design a digital BSF with pass-band edges at f p1 = 0.15 and f p2 = 0.30 and stop-band edges at fs 1 = 0.20 and fs 2 = 0.25. The magnitude response in the pass bands is to stay within 0 and −2 dB, although it must be no larger than −40 dB in the stop band. Let us use the analog type I Chebyshev filter as the prototype filter. Following the same design process as the first example, we have the following.
Finite Wordlength Effects
Practical digital filters must be implemented with finite precision numbers and arithmetic. As a result, both the filter coefficients and the filter input and output signals are in discrete form. This leads to four types of finite wordlength effects.
Discretization (quantization) of the filter coefficients has the effect of perturbing the location of the filter poles and zeroes. As a result, the actual filter response differs slightly from the ideal response. This deterministic frequency response error is referred to as coefficient quantization error.
The use of finite precision arithmetic makes it necessary to quantize filter calculations by rounding or truncation. Roundoff noise is that error in the filter output that results from rounding or truncat- ing calculations within the filter. As the name implies, this error looks like low-level noise at the filter output.
Quantization of the filter calculations also renders the filter slightly nonlinear. For large signals this nonlinearity is negligible and roundoff noise is the major concern. For recursive filters with a zero or constant input, however, this nonlinearity can cause spurious oscillations called limit cycles.
With fixed-point arithmetic it is possible for filter calculations to overflow. The term overflow oscillation, sometimes also called adder overflow limitcycle, refers to a high-level oscillation that can existin another wise stable filter due to the nonlinearity associated with the overflow of internal filter calculations.
In this section we examine each of these finite wordlength effects for both fixed-point and floating-point number representions.
In digital signal processing, (B + 1)-bit fixed-point numbers are usually represented as two’s-complement signed fractions in the format
Floating-point numbers are represented as
In fixed-point arithmetic, a multiply doubles the number of significant bits. For example, the product of the two 5-bit numbers 0.0011 and 0.1001 is the 10-bit number 00.00011011. The extra bit to the left of the decimal point can be discarded without introducing any error. However, the least significant four of the remaining bits must ultimately be discarded by some form of quantization so that the result can be stored to five bits for use in other calculations. In the preceding example this results in 0.0010 (quantization by rounding) or 0.0001 (quantization by truncating). When a sum of products calculation is performed, the quantization can be performed either after each multiply or after all products have been summed with double-length precision.
We will examine the case of fixed-point quantization by rounding. If X is an exact value then the rounded value will be denoted Qr (X). If the quantized value has B bits to the right of the decimal point, the quantization step size is
Since rounding selects the quantized value nearest the unquantized value, it gives a value which is never more than ±Ω/2 away from the exact value. If we denote the rounding error by
error-free calculations that have been corrupted by additive white noise. The mean of this noise for rounding is
With floating-point arithmetic it is necessary to quantize after both multiplications and additions. The addition quantization arises because, prior to addition, the mantissa of the smaller number in the sum is shifted right until the exponent of both numbers is the same. In general, this gives a sum mantissa that is too long and so must be quantized.
We will assume that quantization in floating-point arithmetic is performed by rounding. Because of the exponent in floating-point arithmetic, it is the relative error that is important. The relative error is defined as
Roundoff Noise
To determine the roundoff noise at the output of a digital filter we will assume that the noise due to a quantization is stationary, white, and uncorrelated with the filter input, output, and internal variables. This assumption is good if the filter input changes from sample to sample in a sufficiently complex manner. It is not valid for zero or constant inputs for which the effects of rounding are analyzed from a limit cycle perspective.
To satisfy the assumption of a sufficiently complex input, roundoff noise in digital filters is often calculated for the case of a zero-mean white noise filter input signal x(n) of variance σ 2. This simplifies calculation of the output roundoff noise because expected values of the form E {x(n)x(n − k)} are zero for k =/ 0 and give σ 2 when k = 0. If there is more than one source of roundoff error in a filter, it is assumed that the errors are uncorrelated so that the output noise variance is simply the sum of the contributions from each source. This approach to analysis has been found to give estimates of the output roundoff noise that are close to the noise actually observed in practice.
Another assumption that will be made in calculating round off noise is that the product of two quantization errors is zero. To justify this assumption, consider the case of a 16-bit fixed-point processor. In this case a quantization error is of the order 2−15, whereas the product of two quantization errors is of the order 2−30, which is negligible by comparison.
The simplest case to analyze is a finite impulse response filter realized via the convolution summation
When fixed-point arithmetic is used and quantization is performed after each multiply, the result of the N multiplies is N times the quantization noise of a single multiply. For example, rounding after each multiply gives, from Eqs. (12.29) and (12.33), an output noise variance of
Expanding Eq. (12.44), ignoring products of error terms, and recognizing y(n) gives
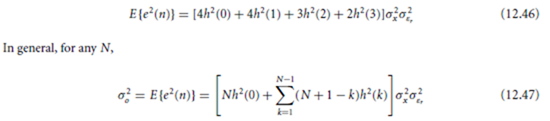
Analysis of roundoff noise for IIR filters proceeds in the same way as for FIR filters. The analysis is more complicated, however, because roundoff noise arising in the computation of internal filter variables (state variables) must be propogated through a transfer function from the point of the quantization to the filter output. This is not necessary for FIR filters realized via the convolution summation since all quantizations are in the output calculation. Another complication in the case of IIR filters realized with fixed-point arithmetic is the need to scale the computation of internal filter variables to avoid their overflow. Examples of roundoff noise analysis for IIR filters can be found in Weinstein and Oppenheim (1969) and Oppenheim and Weinstein (1972) where it is shown that differences in the filter realization structure can make a large difference in the output roundoff noise. In particular, it is shown that IIR filters realized via the parallel or cascade connection of first- and second-order subfilters are almost always superior in terms of roundoff noise to a high-order direct form (single difference equation) realization. It is also possible to choose realizations that are optimal or near optimal in a roundoff noise sense (Mullins and Roberts, 1976; Jackson, Lindgren, and Kim, 1979). These realizations generally require more computation to obtain an output sample from an input sample, however, and so suboptimal realizations with slightly higher roundoff noise are often preferable (Bomar, 1985).
A limit cycle, sometimes referred to as a multiplier roundoff limit cycle, is a low-level oscillation that can exist in an otherwise stable filter as a result of the nonlinearity associated with rounding (or truncating) internal filter calculations (Parker and Hess, 1971). Limit cycles require recursion to exist and do not occur in nonrecursive FIR filters.
As an example of a limit cycle, consider the second-order filter realized by
where δ(n) is the unit impulse or unit sample. The following sequence is obtained:
Notice that although the input is zero except for the first sample, the output oscillates with amplitude 1 /8 and period 6.
Limit cycles are primarily of concern in fixed-point recursive filters. As long as floating-point filters are realized as the parallel or cascade connection of first- and second-order subfilters, limit cycles will generally not be a problem since limit cycles are practically not observable in first- and second-order systems implemented with 32-bit floating-point arithmetic (Bauer, 1993). It has been shown that such systems must have an extremely small margin of stability for limit cycles to exist at anything other than underflow levels, which are at an amplitude of less than 10−38 (Bauer, 1993).
There are at least three ways of dealing with limit cycles when fixed-point arithmetic is used. One is to determine a bound on the maximum limit cycle a mplitude, expressed as an integral number of quantization steps. It is then possible to choose a wordlength that makes the limit cycle amplitude acceptably low. Alternately, limit cycles can be prevented by randomly rounding calculations up or down (Buttner, 1976). This approach, however, is complicated to implement. The third approach is to properly choose the filter realization structure and then quantize the filter calculations using magnitude truncation (Bomar, 1994). This approach has the disadvantage of slightly increasing roundoff noise.
With fixed-point arithmetic it is possible for filter calculations to overflow. This happens when two numbers of the same sign add to give a value having magnitude greater than one. Since numbers with magnitude greater than one are not representable, the result overflows. For example, the two’s complement numbers 0.101 ( 5/8 ) and 0.100 ( 4/8 ) add to give 1.001, which is the two’s complement representation of − 7/8 .
The overflow characteristic of two’s complement arithmetic can be represented as R{} where
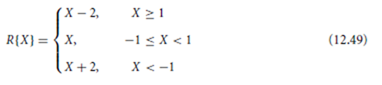
An overflow oscillation, sometimes also referred to as an adder overflow limit cycle, is a high-level oscillation that can exist in an otherwise stable fixed-point filter due to the gross nonlinearity associated with the overflow of internal filter calculations (Ebert, Mazo, and Taylor, 1969). Like limit cycles, overflow oscillations require recursion to exist and do not occur in nonrecursive FIR filters. Overflow oscillations also do not occur with floating-point arithmetic due to the virtual impossibility of overflow.
As an example of an overflow oscillation, once again consider the filter of Eq. (12.48) with four- bit fixed-point two’s complement arithmetic and with the two’s complement overflow characteristic
This is a large-scale oscillation with nearly full-scale amplitude.
There are several ways to prevent overflow oscillations in fixed-point filter realizations. The most obvious is to scale the filter calculations so as to render overflow impossible. However, this may unacceptably restrict the filter dynamic range. Another method is to force completed sums-of-products to saturate at ±1, rather than overflowing (Ritzerfeld, 1989). It is important to saturate only the completed sum, since intermediate overflows in two’s complement arithmetic do not affect the accuracy of the final result. Most fixed-point digital signal processors provide for automatic saturation of completed sums if their saturation arithmetic feature is enabled. Yet another way to avoid overflow oscillations is to use a filter structure for which any internal filter transient is guaranteed to decay to zero (Mills, Mullis, and Roberts, 1978). Such structures are desirable anyway, since they tend to have low roundoff noise and be insensitive to coefficient quantization (Barnes, 1979).
Each filter structure has its own finite, generally nonuniform grids of realizable pole and zero locations when the filter coefficients are quantized to a finite wordlength. In general the pole and zero locations desired in a filter do not correspond exactly to the realizable locations. The error in filter performance (usually measured in terms of a frequency response error) resulting from the placement of the poles and zeroes at the nonideal but realizable locations is referred to as coefficient quantization error.
Consider the second-order filter with complex-conjugate poles
Quantizing the difference equation coefficients results in a nonuniform grid of realizable pole locations in the z plane. The nonuniform grid is defined by the intersection of vertical lines corresponding to quantization of 2λr and concentric circles corresponding to quantization of −r 2. The sparseness of real- izable pole locations near z = ±1 results in a large coefficient quantization error for poles in this region. By contrast, quantizing coefficients of the normal realization (Barnes, 1979) corrresponds to quantizing λr andλi resulting in a uniform grid of realizable pole locations. In this case large coefficient quantization errors are avoided for all pole locations.
It is well established that filter structures with low roundoff noise tend to be robust to coefficient quantization, and vice versa (Jackson, 1976; Rao, 1986). For this reason, the normal (uniform grid) structure is also popular because of its low roundoff noise.
It is well known that in a high-order polynomial with clustered roots the root location is a very sensitive function of the polynomial coefficients. Therefore, filter poles and zeroes can be much more accurately controlled if higher order filters are realized by breaking them up into the parallel or cascade connection of first- and second-order subfilters. One exception to this rule is the case of linear-phase FIR filters in which the symmetry of the polynomial coefficients and the spacing of the filter zeros around the unit circle usually permits an acceptable direct realization using the convolution summation.
Linear-phase FIR digital filters can generally be implemented with acceptable coefficient quantization sensitivity using the direct convolution sum method. When implemented in this way on a digital signal processor, fixed-point arithmetic is not only acceptable but may actually be preferable to floating-point arithmetic. Virtually all fixed-point digital signal processors accumulate a sum of products in a double- length accumulator. Thismeans that only a single quantization is necessary to compute an output. Floating- point arithmetic, on the other hand, requires a quantization after every multiply and after every add in the convolution summation. With 32-bit floating-point arithmetic these quantizations introduce a small enough error to be insignificant for most applications.
When realizing IIR filters, either a parallel or cascade connection of first- and second-order subfilters is almost always preferable to a high-order direct form realization. With the availability of low-cost floating- point digital signal processors, like the Texas Instruments TMS320C32, it is highly recommended that floating-point arithmetic be used for IIR filters. Floating-point arithmetic simultaneously eliminates most concerns regarding scaling, limit cycles, and overflow oscillations. Regardless of the arithmetic employed, a low roundoff noise structure should be used for the second-order sections. The use of a low roundoff noise structure for the second-order sections also tends to give a realization with low coefficient quanti- zation sensitivity. First-order sections are not as critical in determining the roundoff noise and coefficient sensitivity of a realization, and so can generally be implemented with a simple direct form structure.
Adaptive FIR filter: A finite impulse response structure filter with adjustable coefficients. The adjustment is controlled by an adaptation algorithm such as the least mean square (lms) algorithm. They are used extensively in adaptive echo cancellers and equalizers in communication sytems.
Causality: The property of a system that implies that its output can not appear before its input is applied.
This corresponds to an FIR filter with a zero discrete-time impulse response for negative time indices.
Discrete time impulse response: The output of an FIR filter when its input is unity at the first sample and otherwise zero.
Group delay: The group delay of an FIR filter is the negative derivative of the phase response of the filter and is, therefore, a function of the input frequency. At a particular frequency it equals the physical delay that a narrow-band signal will experience passing through the filter.
Linear phase: The phase response of an FIR filter is linearly related to frequency and, therefore, corresponds to constant group delay.
Linear, time invariant (LTI): A system is said to be LTI if superposition holds, that is, its output for an input that consists of the sum of two inputs is identical to the sum of the two outputs that result from the individual application of the inputs; the output is not dependent on the time at that the input is applied. This is the case for an FIR filter with fixed coefficients.
Magnitude response: The change of amplitude, in steady state, of a sinusoid passing through the FIR filter as a function of frequency.
Multirate FIR filter: An FIR filter in which the sampling rate is not constant.
Phase response: The phase change, in steady state, of a sinusoid passing through the FIR filter as a function of frequency.
Antoniou, A. 1993. Digital Filters Analysis, Design, and Applications, 2nd ed. McGraw-Hill, New York. Barnes, C.W. 1979. Roundoff noise and overflow in normal digital filters. IEEE Trans. Circuits Syst. CAS- 26(3):154–159.
Bauer, P.H. 1993. Limit cycle bounds for floating-point implementations of second-order recursive digital filters. IEEE Trans. Circuits Syst.–II 40(8):493–501.
Bomar, B.W. 1985. New second-order state-space structures for realizing low roundoff noise digital filters.
IEEE Trans. Acoust., Speech, Signal Processing ASSP-33(1):106–110.
Bomar, B.W. 1994. Low-roundoff-noise limit-cycle-free implementation of recursive transfer functions on a fixed-point digital signal processor. IEEE Trans. Industrial Electronics 41(1):70–78.
Buttner, M. 1976. A novel approach to eliminate limit cycles in digital filters with a minimum increase in the quantization noise. In Proceedings of the 1976 IEEE International Symposium on Circuits and Systems, pp. 291–294. IEEE, NY.
Cappellini, V., Constantinides, A.G., and Emiliani, P. 1978. Digital Filters and their Applications. Academic Press, New York.
Ebert, P.M., Mazo, J.E., and Taylor, M.G. 1969. Overflow oscillations in digital filters. Bell Syst. Tech. J.
48(9): 2999–3020.
Gray, A.H. and Markel, J.D., 1973. Digital lattice and ladder filter synthesis. IEEE Trans. Acoustics, Speech and Signal Processing ASSP-21:491–500.
Herrmann, O. and Schuessler, W. 1970. Design of nonrecursive digital filters with minimum phase. Electronics Letters 6(11):329–330.
IEEE DSP Committee. 1979. Programs for Digital Signal Processing. IEEE Press, New York.
Jackson, L.B. 1976. Roundoff noise bounds derived from coefficient sensitivities for digital filters. IEEE Trans. Circuits Syst. CAS-23(8):481–485.
Jackson, L.B., Lindgren, A.G., and Kim, Y. 1979. Optimal synthesis of second-order state-space structures for digital filters. IEEE Trans. Circuits Syst. CAS-26(3):149–153.
Lee, E.A. and Messerschmitt, D.G. 1994. Digital Communications, 2nd ed. Kluwer, Norwell, MA.
Macchi, O. 1995. Adaptive Processing: The Least Mean Squares Approach with Applications in Telecommunications, Wiley, New York.
Mills, W.T., Mullis, C.T., and Roberts, R.A. 1978. Digital filter realizations without overflow oscillations.
IEEE Trans. Acoust., Speech, Signal Processing. ASSP-26(4):334–338.
Mullis, C.T. and Roberts, R.A. 1976. Synthesis of minimum roundoff noise fixed-point digital filters. IEEE Trans. Circuits Syst. CAS-23(9):551–562.
Oppenheim, A.V. and Schafer, R.W. 1989. Discrete-Time Signal Processing. Prentice-Hall, Englewood Cliffs, NJ.
Oppenheim, A.V. and Weinstein, C.J. 1972. Effects of finite register length in digital filtering and the fast fourier transform. Proc. IEEE 60(8):957–976.
Parker, S.R. and Hess, S.F. 1971. Limit-cycle oscillations in digital filters. IEEE Trans. Circuit Theory CT- 18(11):687–697.
Parks, T.W. and Burrus, C.S. 1987. Digital Filter Design. Wiley, New York.
Parks, T.W. and McClellan, J.H. 1972a. Chebyshev approximations for non recursive digital filters with linear phase. IEEE Trans. Circuit Theory CT-19:189–194.
Parks, T.W. and McClellan, J.H. 1972b. A program for the design of linear phase finite impulse response filters. IEEE Trans. Audio Electroacoustics AU-20(3):195–199.
Proakis, J.G. and Manolakis, D.G. 1992. Digital Signal Processing Principles, Algorithms, and Applications, 2nd ed. MacMillan, New York.
Rabiner, L.R. and Gold, B. 1975. Theory and Application of Digital Signal Processing. Prentice-Hall, Engle- wood Cliffs, NJ.
Rabiner, L.R. and Schafer, R.W. 1978. Digital Processing of Speech Signals. Prentice-Hall, Englewood Cliffs, NJ.
Rabiner, L.R. and Schafer, R.W. 1974. On the behavior of minimax FIR digital Hilbert transformers. Bell Sys. Tech. J. 53(2):361–388.
Rao, D.B.V. 1986. Analysis of coefficient quantization errors in state-space digital filters. IEEE Trans. Acoust., Speech, Signal Processing ASSP-34(1):131–139.
Ritzerfeld, J.H.F. 1989. A condition for the overflow stability of second-order digital filters that is satisfied by all scaled state-space structures using saturation. IEEE Trans. Circuits Syst. CAS-36(8): 1049–1057.
Roberts, R.A. and Mullis, C.T. 1987. Digital Signal Processing. Addison-Wesley, Reading, MA. Vaidyanathan, P.P. 1993. Multirate Systems and Filter Banks. Prentice-Hall, Englewood Cliffs, NJ.
Weinstein, C. and Oppenheim, A.V. 1969. A comparison of round off noise in floating-point and fixed-point digital filter realizations. Proc. IEEE 57(6):1181–1183.
Additional information on the topic of digital filters is available from the following sources.
IEEE Transactionson Signal Processing, amonthly publication of the Institute of Electrical and Electronics Engineers, Inc, Corporate Office, 345 East 47 Street, NY.
IEEE Transactions on Circuits and Systems—Part II: Analog and Digital Signal Processing, a monthly publication of the Institute of Electrical and Electronics Engineers, Inc, Corporate Office, 345 East 47 Street, NY.
The Institute of Electrical and Electronics Engineers holds an annual conference at worldwide locations called the International Conference on Acoustics, Speech and Signal Processing, ICASSP, Corporate Office, 345 East 47 Street, NY.
IEE Transactions on Vision, Image and Signal Processing,a monthly publication of the Institute of Electrical Engineers, Head Office, Michael Faraday House, Six Hills Way, Stevenage, UK.
Signal Processing, a publication of the European Signal Processing Society, Switzerland, Elsevier Science B.V., Journals Dept., P.O. Box 211, 1000 AE Amsterdam, The Netherlands.
In addition, the following books are recommended.
Bellanger, M. 1984. Digital Processing of Signals: Theory and Practice. Wiley, New York.
Burrus, C.S. et al. 1994. Computer-Based Exercises for Signal Processing Using MATLAB. Prentice-Hall, Englewood Cliffs, NJ.
Jackson, L.B. 1986. Digital Filters and Signal Processing. Kluwer Academic, Norwell, MA, 1986.
Oppenheim, A.V. and Schafer, R.W. 1989. Discrete-Time Signal Processing. Prentice-Hall, Englewood Cliffs, NJ.
Widrow, B. and Stearns, S. 1985. Adaptive Signal Processing. Prentice-Hall, Englewood Cliffs, NJ.
Labels: Digital Filters
