EFFECT OF A LOAD
When a load device is connected across the secondary winding of a transformer, current flows through the secondary and the load. The magnetic field produced by the current in the secondary interacts with the magnetic field produced by the current in the primary. This interaction results from the mutual inductance between the primary and secondary windings.
MUTUAL FLUX
The total flux in the core of the transformer is common to both the primary and secondary windings. It is also the means by which energy is transferred from the primary winding to the secondary winding. Since this flux links both windings, it is called MUTUAL FLUX. The inductance which produces this flux is also common to both windings and is called mutual inductance.
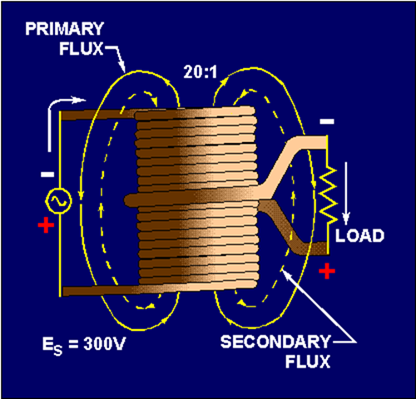
Figure 5-11 shows the flux produced by the currents in the primary and secondary windings of a transformer when source current is flowing in the primary winding.
Figure 5-11. - Simple transformer indicating primary- and secondary-winding flux relationship.
When a load resistance is connected to the secondary winding, the voltage induced into the secondary winding causes current to flow in the secondary winding. This current produces a flux field about the secondary (shown as broken lines) which is in opposition to the flux field about the primary (Lenz's law). Thus, the flux about the secondary cancels some of the flux about the primary. With less flux surrounding the primary, the counter emf is reduced and more current is drawn from the source. The additional current in the primary generates more lines of flux, nearly reestablishing the original number of total flux lines.
TURNS AND CURRENT RATIOS
The number of flux lines developed in a core is proportional to the magnetizing force (IN AMPERE-TURNS) of the primary and secondary windings.
The ampere-turn (I X N) is a measure of magnetomotive force; it is defined as the magnetomotive force developed by one ampere of current flowing in a coil of one turn. The flux which exists in the core of a transformer surrounds both the primary and secondary windings. Since the flux is the same for both windings, the ampere-turns in both the primary and secondary windings must be the same.
Therefore:


Notice the equations show the current ratio to be the inverse of the turns ratio and the voltage ratio. This means, a transformer having less turns in the secondary than in the primary would step down the voltage, but would step up the current. Example: A transformer has a 6:1 voltage ratio.

The above equations can be looked at from another point of view.
The expression
<figureeq4">
is called the transformer TURNS RATIO and may be expressed as a single factor. Remember, the turns ratio indicates the amount by which the transformer increases or decreases the voltage applied to the primary. For example, if the secondary of a transformer has two times as many turns as the primary, the voltage induced into the secondary will be two times the voltage across the primary. If the secondary has one-half as many turns as the primary, the voltage across the secondary will be one-half the voltage across the primary. However, the turns ratio and the current ratio of a transformer have an inverse relationship. Thus, a 1:2 step-up transformer will have one-half the current in the secondary as in the primary. A 2:1 step-down transformer will have twice the current in the secondary as in the primary.
Example: A transformer with a turns ratio of 1:12 has 3 amperes of current in the secondary. What is the value of current in the primary?
Q.20 A transformer with a turns ratio of 1:3 has what current ratio? Q.21 A transformer has a turns ratio of 5:1 and a current of 5 amperes flowing in the secondary. What is the current flowing in the primary? (Assume no losses)
Back
Home
Up
Next
POWER RELATIONSHIP BETWEEN PRIMARY AND SECONDARY WINDINGS
As just explained, the turns ratio of a transformer affects current as well as voltage. If voltage is doubled in the secondary, current is halved in the secondary. Conversely, if voltage is halved in the secondary, current is doubled in the secondary. In this manner, all the power delivered to the primary by the source is also delivered to the load by the secondary (minus whatever power is consumed by the transformer in the form of losses). Refer again to the transformer illustrated in figure 5-11.
The turns ratio is 20:1. If the input to the primary is 0.1 ampere at 300 volts, the power in the primary is P = E X I = 30 watts. If the transformer has no losses, 30 watts is delivered to the secondary. The secondary steps down the voltage to 15 volts and steps up the current to 2 amperes. Thus, the power delivered to the load by the secondary is P = E X I = 15 volts X 2 amps = 30 watts.
The reason for this is that when the number of turns in the secondary is decreased, the opposition to the flow of the current is also decreased.
Hence, more current will flow in the secondary. If the turns ratio of the transformer is increased to 1:2, the number of turns on the secondary is twice the number of turns on the primary. This means the opposition to current is doubled. Thus, voltage is doubled, but current is halved due to the increased opposition to current in the secondary. The important thing to remember is that with the exception of the power consumed within the transformer, all power delivered to the primary by the source will be delivered to the load. The form of the power may change, but the power in the secondary almost equals the power in the primary.
TRANSFORMER LOSSES
Practical power transformers, although highly efficient, are not perfect devices. Small power transformers used in electrical equipment have an 80 to 90 percent efficiency range, while large, commercial powerline transformers may have efficiencies exceeding 98 percent.
The total power loss in a transformer is a combination of three types of losses. One loss is due to the dc resistance in the primary and secondary windings. This loss is called COPPER loss or I2R loss.
The two other losses are due to EDDY CURRENTS and to HYSTERESIS in the core of the transformer. Copper loss, eddy-current loss, and hysteresis loss result in undesirable conversion of electrical energy into heat energy.
Q.22 What is the mathematical relationship between the power in the primary (Pp) and power in the secondary (Ps) of a transformer?
Copper Loss
Whenever current flows in a conductor, power is dissipated in the resistance of the conductor in the form of heat. The amount of power dissipated by the conductor is directly proportional to the resistance of the wire, and to the square of the current through it. The greater the value of either resistance or current, the greater is the power dissipated. The primary and secondary windings of a transformer are usually made of low-resistance copper wire.
The resistance of a given winding is a function of the diameter of the wire and its length. Copper loss can be minimized by using the proper diameter wire. Large diameter wire is required for high-current windings, whereas small diameter wire can be used for low-current windings.
Eddy-Current Loss
The core of a transformer is usually constructed of some type of ferromagnetic material because it is a good conductor of magnetic lines of flux.
Whenever the primary of an iron-core transformer is energized by an alternating-current source, a fluctuating magnetic field is produced. This magnetic field cuts the conducting core material and induces a voltage into it. The induced voltage causes random currents to flow through the core which dissipates power in the form of heat. These undesirable currents are called
EDDY CURRENTS.
To minimize the loss resulting from eddy currents, transformer cores are LAMINATED. Since the thin, insulated laminations do not provide an easy path for current, eddy-
Format current losses are greatly reduced.
Hysteresis Loss
When a magnetic field is passed through a core, the core material becomes magnetized. To become magnetized, the domains within the core must align themselves with the external field. If the direction of the field is reversed, the domains must turn so that their poles are aligned with the new direction of the external field.
Power transformers normally operate from either 60 Hz, or 400 Hz alternating current. Each tiny domain must realign itself twice during each cycle, or a total of 120 times a second when 60 Hz alternating current is used. The energy used to turn each domain is dissipated as heat within the iron core. This loss, called HYSTERESIS LOSS, can be thought of as resulting from molecular friction. Hysteresis loss can be held to a small value by proper choice of core materials.
TRANSFORMER EFFICIENCY
To compute the efficiency of a transformer, the input power to and the output power from the transformer must be known. The input power is equal to the product of the voltage applied to the primary and the current in the primary. The output power is equal to the product of the voltage across the secondary and the current in the secondary. The difference between the input power and the output power represents a power loss. You can calculate the percentage of efficiency of a transformer by using the standard efficiency formula shown below:

Example. If the input power to a transformer is 650 watts and the output power is 610 watts, what is the efficiency?

Q.23 Name the three power losses in a transformer.
Q.24 The input power to a transformer is 1,000 watts and the output power is 500 watts. What is the efficiency of the transformer, expressed as a percentage?
Labels: TRANSFORMERS