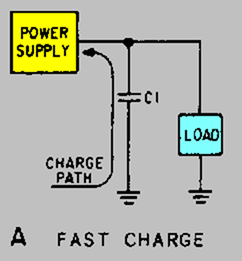
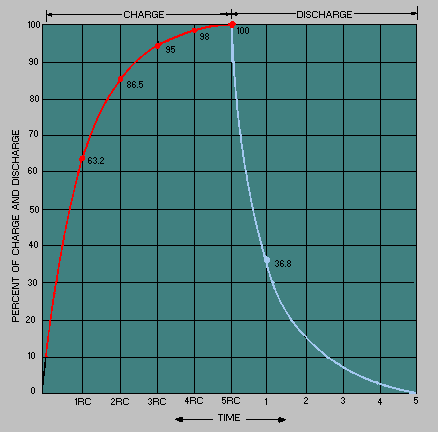
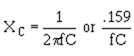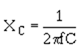You should also recall that a capacitor is considered fully charged after five RC time constants. Refer to figure 4-11. You can see that a steady dc output voltage is obtained when the capacitor charges rapidly and discharges as slowly as possible.
Figure 4-11. - RC time constant.
In filter circuits the capacitor is the common element to both the charge and the discharge paths. Therefore, to obtain the longest possible discharge time, you want the capacitor to be as large as possible. Another way to look at it is: The capacitor acts as a short circuit around the load (as far as the ac component is concerned), and since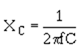
the larger the value of the capacitor (C), the smaller the opposition (XC) or reactance to ac.
Now let's look at inductors and their application in filter circuits.
Remember, AN INDUCTOR OPPOSES ANY CHANGE IN CURRENT. In case you have forgotten, a change in current through an inductor produces a changing electromagnetic field. The changing field, in turn, cuts the windings of the wire in the inductor and thereby produces a counter electromotive force (CEMF). It is the CEMF that opposes the change in circuit current. Opposition to a change in current at a given frequency is called inductive reactance (XL) and is measured in ohms. The inductive reactance (XL) of an inductor is determined by the applied frequency and the inductance of the inductor.
Mathematically,
XL = 2πfL
If frequency or inductance is increased, the XL increases. Since inductors are placed in series with the load (as shown in figure 4-12), the larger the XL, the larger the ac voltage developed across the load.
Figure 4-12. - Voltage drops in an inductive filter.

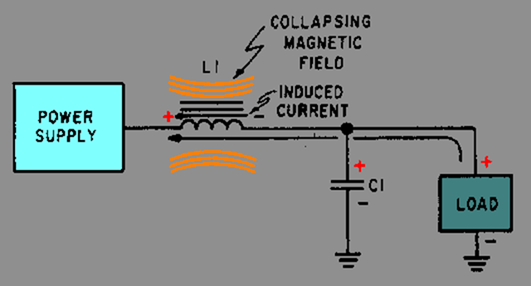
Now refer to figure 4-13. When the current starts to flow through the coil, an expanding magnetic field builds up around the inductor. This magnetic field around the coil develops the CEMF that opposes the change in current. When the rectifier current decreases, as shown in figure 4-14, the magnetic field collapses and again cuts the turns (windings) of wire, thus inducing current into the coil. This additional current merges with the rectifier current and attempts to keep it at its original level.
Figure 4-13. - Inductive filter (expanding field).
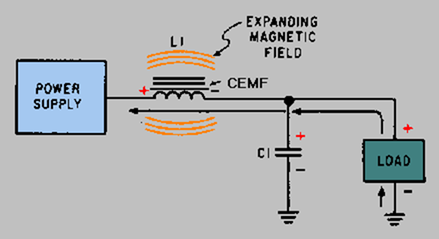
Figure 4-14. - Inductive filter (collapsing field).
Now that you have read how the components in a filter circuit react to current flow from the rectifier, the different types of filter circuits in use today will be discussed.
Q.13 If you increase the value of the capacitor, will the XC increase or decrease? Why?
Back
Home
Up
Next
The Capacitor Filter
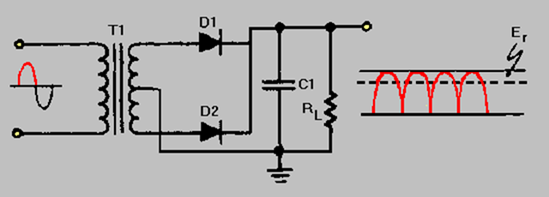
The simple capacitor filter is the most basic type of power supply filter. The application of the simple capacitor filter is very limited. It is sometimes used on extremely high-voltage, low-current power supplies for cathode-ray and similar electron tubes, which require very little load current from the supply. The capacitor filter is also used where the power-supply ripple frequency is not critical; this frequency can be relatively high. The capacitor (C1) shown in figure 4-15 is a simple filter connected across the output of the rectifier in parallel with the load.
Figure 4-15. - Full-wave rectifier with a capacitor filter.
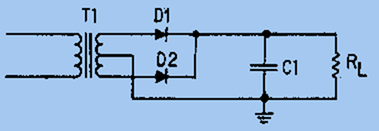
When this filter is used, the RC charge time of the filter capacitor (C1) must be short and the RC discharge time must be long to eliminate ripple action. In other words, the capacitor must charge up fast, preferably with no discharge at all. Better filtering also results when the input frequency is high; therefore, the full-wave rectifier output is easier to filter than that of the half-wave rectifier because of its higher frequency.
For you to have a better understanding of the effect that filtering has on Eavg, a comparison of a rectifier circuit with a filter and one without a filter is illustrated in views A and B of figure 4-16. The output waveforms in figure 4-16 represent the unfiltered and filtered outputs of the half-wave rectifier circuit. Current pulses flow through the load resistance (RL) each time a diode conducts. The dashed line indicates the average value of output voltage. For the half-wave rectifier, Eavg is less than half (or approximately 0.318) of the peak output voltage. This value is still much less than that of the applied voltage. With no capacitor connected across the output of the rectifier circuit, the waveform in view A has a large pulsating component (ripple) compared with the average or dc component. When a capacitor is connected across the output (view B), the average value of output voltage (Eavg) is increased due to the filtering action of capacitor C1.
Figure 4-16A. - Half-wave rectifier with and without filtering.
UNFILTERED

Figure 4-16B. - Half-wave rectifier with and without filtering.
FILTERED

The value of the capacitor is fairly large (several microfarads), thus it presents a relatively low reactance to the pulsating current and it stores a substantial charge.
The rate of charge for the capacitor is limited only by the resistance of the conducting diode which is relatively low. Therefore, the RC charge time of the circuit is relatively short. As a result, when the pulsating voltage is first applied to the circuit, the capacitor charges rapidly and almost reaches the peak value of the rectified voltage within the first few cycles. The capacitor attempts to charge to the peak value of the rectified voltage anytime a diode is conducting, and tends to retain its charge when the rectifier output falls to zero. (The capacitor cannot discharge immediately.) The capacitor slowly discharges through the load resistance (RL) during the time the rectifier is nonconducting.
The rate of discharge of the capacitor is determined by the value of capacitance and the value of the load resistance. If the capacitance and load-resistance values are large, the RC discharge time for the circuit is relatively long.
A comparison of the waveforms shown in figure 4-16 (view A and view B) illustrates that the addition of C1 to the circuit results in an increase in the average of the output voltage (Eavg) and a reduction in the amplitude of the ripple component (Er) which is normally present across the load resistance.
Now, let's consider a complete cycle of operation using a half-wave rectifier, a capacitive filter (C1), and a load resistor (RL). As shown in view A of figure 4-17, the capacitive filter (C1) is assumed to be large enough to ensure a small reactance to the pulsating rectified current. The resistance of RL is assumed to be much greater than the reactance of C1 at the input frequency. When the circuit is energized, the diode conducts on the positive half cycle and current flows through the circuit, allowing C1 to charge. C1 will charge to approximately the peak value of the input voltage. (The charge is less than the peak value because of the voltage drop across the diode (D1)). In view A of the figure, the charge on C1 is indicated by the heavy solid line on the waveform. As illustrated in view B, the diode cannot conduct on the negative half cycle because the anode of D1 is negative with respect to the cathode. During this interval, C1 discharges through the load resistor (RL). The discharge of C1 produces the downward slope as indicated by the solid line on the waveform in view B. In contrast to the abrupt fall of the applied ac voltage from peak value to zero, the voltage across C1 (and thus across RL) during the discharge period gradually decreases until the time of the next half cycle of rectifier operation. Keep in mind that for good filtering, the filter capacitor should charge up as fast as possible and discharge as little as possible.
Figure 4-17A. - Capacitor filter circuit (positive and negative half cycles). POSITIVE HALF-CYCLE

Figure 4-17B. - Capacitor filter circuit (positive and negative half cycles). NEGATIVE HALF-CYCLE

Since practical values of C1 and RL ensure a more or less gradual decrease of the discharge voltage, a substantial charge remains on the capacitor at the time of the next half cycle of operation. As a result, no current can flow through the diode until the rising ac input voltage at the anode of the diode exceeds the voltage on the charge remaining on C1. The charge on C1 is the cathode potential of the diode. When the potential on the anode exceeds the potential on the cathode (the charge on C1), the diode again conducts, and C1 begins to charge to approximately the peak value of the applied voltage.
After the capacitor has charged to its peak value, the diode will cut off and the capacitor will start to discharge. Since the fall of the ac input voltage on the anode is considerably more rapid than the decrease on the capacitor voltage, the cathode quickly become more positive than the anode, and the diode ceases to conduct.
Operation of the simple capacitor filter using a full-wave rectifier is basically the same as that discussed for the half-wave rectifier. Referring to figure 4-18, you should notice that because one of the diodes is always conducting on. either alternation, the filter capacitor charges and discharges during each half cycle. (Note that each diode conducts only for that portion of time when the peak secondary voltage is greater than the charge across the capacitor.)
Figure 4-18. - Full-wave rectifier (with capacitor filter).
Another thing to keep in mind is that the ripple component (E r) of the output voltage is an ac voltage and the average output voltage (Eavg) is the dc component of the output. Since the filter capacitor offers a relatively low impedance to ac, the majority of the ac component flows through the filter capacitor. The ac component is therefore bypassed (shunted) around the load resistance, and the entire dc component (or Eavg) flows through the load resistance. This statement can be clarified by using the formula for XC in a half-wave and full-wave rectifier. First, you must establish some values for the circuit.


As you can see from the calculations, by doubling the frequency of the rectifier, you reduce the impedance of the capacitor by one-half. This allows the ac component to pass through the capacitor more easily. As a result, a full-wave rectifier output is much easier to filter than that of a half-wave rectifier. Remember, the smaller the XC of the filter capacitor with respect to the load resistance, the better the filtering action. Since
the largest possible capacitor will provide the best filtering.
Remember, also, that the load resistance is an important consideration. If load resistance is made small, the load current increases, and the average value of output voltage (Eavg) decreases. The RC discharge time constant is a direct function of the value of the load resistance; therefore, the rate of capacitor voltage discharge is a direct function of the current through the load. The greater the load current, the more rapid the discharge of the capacitor, and the lower the average value of output voltage. For this reason, the simple capacitive filter is seldom used with rectifier circuits that must supply a relatively large load current. Using the simple capacitive filter in conjunction with a full-wave or bridge rectifier provides improved filtering because the increased ripple frequency decreases the capacitive reactance of the filter capacitor.
Q.14 What is the most basic type of filter?
Q.15 In a capacitor filter, is the capacitor in series or in parallel with the load?
Q.16 Is filtering better at a high frequency or at a low frequency?
Q.17 Does a filter circuit increase or decrease the average output voltage?
Q.18 What determines the rate of discharge of the capacitor in a filter circuit?
Q.19 Does low ripple voltage indicate good or bad filtering?
Q.20 Is a full-wave rectifier output easier to filter than that of a half-wave rectifier?
Back
Home
Up
Next
LC Choke-Input Filter
The LC choke-input filter is used primarily in power supplies where voltage regulation is important and where the output current is relatively high and subject to varying load conditions. This filter is used in high power applications such as those found in radars and communication transmitters.
Notice in figure 4-19 that this filter consists of an input inductor (L1), or filter choke, and an output filter capacitor (C1). Inductor L1 is placed at the input to the filter and is in series with the output of the rectifier circuit. Since the action of an inductor is to oppose any change in current flow, the inductor tends to keep a constant current flowing to the load throughout the complete cycle of the applied voltage. As a result, the output voltage never reaches the peak value of the applied voltage. Instead, the output voltage approximates the average value of the rectified input to the filter, as shown in the figure. The reactance of the inductor (XL) reduces the amplitude of ripple voltage without reducing the dc output voltage by an appreciable amount. (The dc resistance of the inductor is just a few ohms.)
Figure 4-19. - LC choke-input filter.
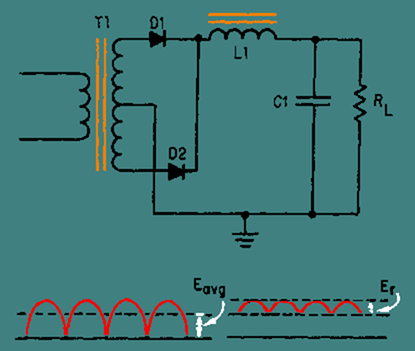
The shunt capacitor (C1) charges and discharges at the ripple frequency rate, but the amplitude of the ripple voltage (Er) is relatively small because the inductor (L1) tends to keep a constant current flowing from the rectifier circuit to the load. In addition, the reactance of the shunt capacitor (XC) presents a low impedance to the ripple component existing at the output of the filter, and thus shunts the ripple component around the load. The capacitor attempts to hold the output voltage relatively constant at the average value of the voltage.
The value of the filter capacitor (C1) must be relatively large to present a low opposition (XC) to the pulsating current and to store a substantial charge. The rate of the charge for the capacitor is limited by the low impedance of the ac source (the transformer), by the small resistance of the diode, and by the counter electromotive force (CEMF) developed by the coil. Therefore, the RC charge time constant is short compared to its discharge time. (This comparison in RC charge and discharge paths is illustrated in views A and B of figure 4-20.) Consequently, when the pulsating voltage is first applied to the LC choke-input filter, the inductor (L1) produces a CEMF which opposes the constantly increasing input voltage. The net result is to effectively prevent the rapid charging of the filter capacitor (C1). Thus, instead of reaching the peak value of the input voltage, C1 only charges to the average value of the input voltage. After the input voltage reaches its peak and decreases sufficiently, the capacitor C1) attempts to discharge through the load resistance RL). C1 will only partially discharge, as indicated in view B of the figure, because of its relatively long discharge time constant. The larger the value of the filter capacitor, the better the filtering action. However, because of physical size, there is a practical limitation to the maximum value of the capacitor.
Figure 4-20A. - LC choke-input filter (charge and discharge paths).
CHARGE PATH

Figure 4-20B. - LC choke-input filter (charge and discharge paths).
DISCHARGE PATH

The inductor (also referred to as the filter choke or coil) serves to maintain the current flow to the filter output (RL) at a nearly constant level during the charge and discharge periods of the filter capacitor. The inductor (L1) and the capacitor (C1) form a voltage divider for the ac component (ripple) of the applied input voltage. This is shown in views A and B of figure 4-21. As far as the ripple component is concerned, the inductor offers a high impedance (Z) and the capacitor offers a low impedance (view B). As a result, the ripple component (Er) appearing across the load resistance is greatly attenuated (reduced). The inductance of the filter choke opposes changes in the value of the current flowing through it; therefore, the average value of the voltage produced across the capacitor contains a much smaller value of ripple component (Er) than the value of ripple produced across the choke.
Figure 4-21. - LC choke-input filter.

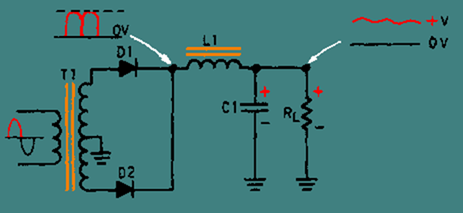
Now look at figure 4-22 which illustrates a complete cycle of operation for a full-wave rectifier circuit used to supply the input voltage to the filter. The rectifier voltage is developed across the capacitor (C1). The ripple voltage at the output of the filter is the alternating component of the input voltage reduced in amplitude by the filter section. Each time the anode of a diode goes positive with respect to the cathode, the diode conducts and C1 charges. Conduction occurs twice during each cycle for a full-wave rectifier. For a 60-hertz supply, this produces a 120-hertz ripple voltage. Although the diodes alternate (one conducts while the other is nonconducting), the filter input voltage is not steady. As the anode voltage of the conducting diode increases (on the positive half of the cycle), capacitor C1 charges-the charge being limited by the impedance of the secondary transformer winding, the diode's forward (cathode-to-anode) resistance, and the counter electromotive force developed by the choke. During the nonconducting interval (when the anode voltage drops below the capacitor charge voltage), C1 discharges through the load resistor (RL). The components in the discharge path have a long time constant; thus, C1 discharges more slowly than it charges.
Figure 4-22. - Filtering action of the LC choke-input filter.
The choke (L1) is usually a large value, from 1 to 20 henries, and offers a large inductive reactance to the 120-hertz ripple component produced by the rectifier. Therefore, the effect that L1 has on the charging of the capacitor (C1) must be considered. Since L1 is connected in series with the parallel branch consisting of C1 and RL, a division of the ripple (ac) voltage and the output (dc) voltage occurs. The greater the impedance of the choke, the less the ripple voltage that appears across C1 and the output. The dc output voltage is fixed mainly by the dc resistance of the choke.
Now that you have read how the LC choke-input filter functions, it will be discussed with actual component values applied. For simplicity, the input frequency at the primary of the transformer will be 117 volts 60 hertz. Both half-wave and full-wave rectifier circuits will be used to provide the input to the filter.
Starting with the half-wave configuration shown in figure 4-23 , the basic parameters are: With 117 volts ac rms applied to the T1 primary, 165 volts ac peak is available at the secondary [(117 V) X (1.414) = 165 V]. You should recall that the ripple frequency of this half-wave rectifier is 60 hertz. Therefore, the capacitive reactance of C1 is:

Figure 4-23. - Half-wave rectifier with an LC choke-input filter.
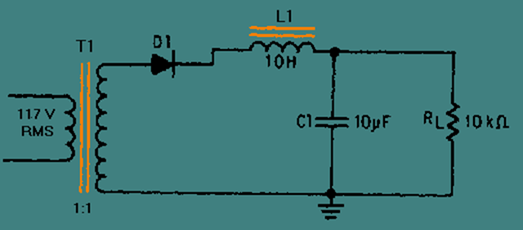
This means that the capacitor (C1) offers 265 ohms of opposition to the ripple current. Note, however, that the capacitor offers an infinite impedance to direct current. The inductive reactance of L1 is:

The above calculation shows that L1 offers a relatively high opposition (3.8 kilohms) to the ripple in comparison to the opposition offered by C1 (265 ohms). Thus, more ripple voltage will be dropped across L1 than across C1. In addition, the impedance of C1 (265 ohms) is relatively low with respect to the resistance of the load (10 kilohms). Therefore, more ripple current flows through C1 than the load. In other words, C1 shunts most of the ac component around the load.
Back
Home
Up
Next