DIELECTRIC CHARACTERISTICS
Three factors were shown to affect the capacitance of a capacitor. One factor is the type of insulating material used for the dielectric. Most capacitors are constructed using a dielectric material having a higher dielectric constant than air.
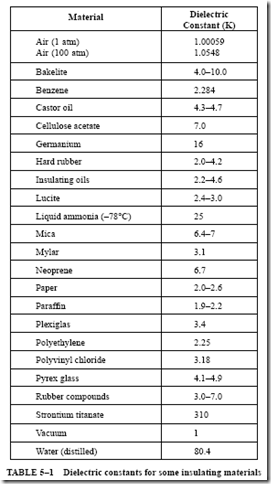
The dielectric constant of an insulating material measures the effectiveness of the material when it is used as the dielectric of a capacitor. It is assumed that air has a dielectric constant of one. If a two-plate capacitor has a dielectric consisting of paper impregnated
with paraffin, rather than a dielectric of air, the capacitance will increase. If the capacitance is doubled when using paper in place of air for the dielectric, the dielectric constant for paper is 2. This value indicates the degree of distortion of the electron orbits in the dielectric for a given applied voltage. Table 5–1 lists the dielectric constants of some insulating materials.
Dielectric Strength
If the voltage across the plates of a capacitor becomes too high, the dielectric may be burned or punctured by the high potential. That is, the high potential tears electrons from the orbits of the atoms of the dielectric material. As a result, the dielectric becomes a con- ducting material, resulting in permanent damage to the dielectric.
Dielectric materials are given a dielectric strength rating. This rating is stated as either “volts per centimeter” or “volts per mil” of thickness required to break down the dielectric. The dielectric strength rating is not the same as the dielectric constant rating. For example, the dielectric constant of paper is about 2 and that of Pyrex glass is approximately 4. However, the dielectric strength in volts per mil for some kinds of paper is about 1200 V. For Pyrex glass, the dielectric strength is only 325 V per mil.
CAPACITANCE FORMULAS
The capacitance of a two-plate capacitor is directly proportional to the area of one plate and inversely proportional to the distance of separation between the plates.
This statement can be expressed as a formula. Actually, there are two forms of the formula, depending on the units of measurement for the distances involved. To determine the capacitance in picofarads when the plate dimensions and the distance between the plates are given in inches, the formula is
Statement of the Problem
A paper capacitor consists of two tinfoil plates, each 8 feet (ft) long and 1 inch (in.) wide. The waxed paper that separates the two plates has a thickness of 0.05 in. Determine the capacitance of the capacitor. The dielectric constant of waxed paper is 2.
Solution
CAPACITORS IN PARALLEL
In addition to increasing the plate area, an increase in capacitance can be obtained by increasing the number of plates in the capacitor.
The multiple plates of the capacitor shown in Figure 5–7 are placed so that a maxi- mum plate area is obtained. Note that alternate plates are connected in parallel. To calculate
the capacitance of a multiplate capacitor, where the plates are identical and are separated by the same distance, the following expression is used:
Labels: ALTERNATING CURRENT GENERATORS