A capacitor connected to an ac supply repeatedly charges and discharges as the ac voltage changes direction. The charging current also alternates in direction as the capacitor charges and discharges.
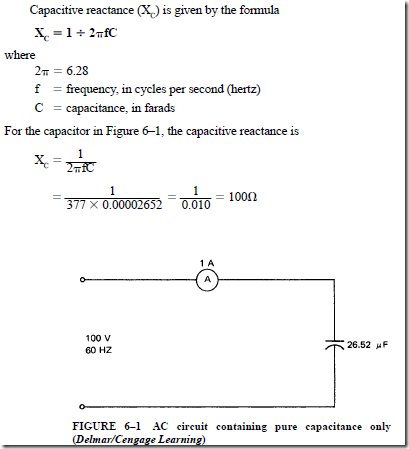
In the circuit in Figure 6–1, a 26.52-f.LF capacitor is connected across a 100-V, 60-Hz source. The ammeter indicates a current of one ampere. The dielectric of the capacitor prevents electrons from being conducted through the capacitor. However, there is elec- tron flow to and from the plates of the capacitor as it charges and discharges in each cycle. The opposition voltage increases as the electrostatic field builds up across the plates. This voltage opposes the line voltage and limits the current. The opposition voltage that develops with a capacitor is really a countervoltage.
Inductance in an ac circuit also causes a countervoltage. The current-limiting effect of this countervoltage is measured as ohms of inductive reactance. The current-limiting effect of capacitance in an ac circuit is called capacitive reactance and is measured in ohms.
Current in the Capacitive Circuit
The current, in amperes, in an ac circuit containing capacitance is determined using a form of Ohm’s law. That is, capacitive reactance (X ) is substituted for resistance (R) as follows:
The formula for capacitive reactance shows that the value in ohms is inversely proportional to the capacitance in farads and the frequency of the impressed ac voltage. This relationship is logical because the charge on a capacitor is directly proportional to the capacitance for a given applied voltage. The pattern of this charge is an alternating current as the applied voltage alternates. If the capacitance increases for a given frequency and voltage, then the charge that flows in a given time must also increase. Thus, the current increases. If the frequency increases for a given capacitance and voltage, the same charge must flow per voltage alternation, but in a shorter time. Thus, an increase in frequency results in a larger current because current is a measure of the rate of flow of electrons.
An increase in either the frequency or the capacitance gives rise to an increase in current for a given applied voltage. It follows that an increase in the frequency or capaci- tance results in a decrease of the capacitive reactance (ohms).
LEADING CURRENT
The capacitor shown in Figure 6–1 has a capacitive reactance of 100 !1 and negligible resistance. The current in this circuit is one ampere. It was shown earlier in this text that the current in a pure resistive load is in phase with the voltage. In addition, it was shown that the current through a pure inductive reactance lags the impressed voltage by 90 electrical degrees. This unit will show that in a circuit with pure capacitive reactance, the current will lead the impressed voltage by 90 electrical degrees.
Alternating Voltage Applied to a Capacitor
A capacitor is charged when a dc voltage is applied to its terminals. The capacitor is discharged if a resistor is connected across its terminals. When an alternating voltage is applied to a capacitor, an alternating current of the same frequency repeatedly charges and discharges the capacitor. The charge in coulombs on the capacitor is proportional to the impressed voltage. As shown in Figure 6–2, the charge in coulombs is in phase with the impressed voltage (Q C X V). At zero voltage, the charge in coulombs is also zero. At the maximum positive and negative values of impressed voltage, the charge in coulombs is also at maximum.
Operation from 0° to 180°. The wave patterns for the impressed voltage and the charge are shown in Figure 6–2. The current is shown leading the line voltage by 90 electrical degrees. In the interval from 0° to 90°, the impressed voltage increases and the capacitor is charging. At 90° the capacitor voltage no longer increases. At this point, then, the cur- rent is zero. As the impressed voltage starts to decrease, the capacitor starts to discharge.
The electrons now flow from the plates in a direction reversed from the initial charging direction. This is shown by the current as it increases in the negative (discharging) direction. At the same time, the impressed voltage decreases to zero during the interval from 90° to 180°.
Operation from 180° to 360°. At 180°, the line voltage is zero. The charge, in coulombs, is zero and the current is at its maximum value. The capacitor now begins to charge in the opposite direction, and the impressed voltage starts to rise toward its negative maximum value. The current is in the same direction as the impressed voltage in the range from 180° to 270°. The current decreases in magnitude as the rate of change of voltage decreases. At 270 electrical degrees, the capacitor voltage no longer increases. Therefore, the current is zero at 270°. Between 270° and 360°, the voltage again decreases to zero. As the negative charge is removed from the capacitor, the capacitor current increases in a positive direction. The capacitor voltage decreases to zero and the current rises in the positive direction to its maximum value at 360°. The capacitor is completely discharged at 360°.
ANGLE OF PHASE DEFECT
For circuits containing inductance coils, both the resistance and the inductive reactance must be considered. For circuits containing capacitors operating at commercial power frequencies, the resistance losses are usually assumed to be negligible. At such frequencies, the capacitor current leads the capacitor voltage by 90 electrical degrees.
Under actual operating conditions, the angle by which the capacitor current leads the voltage is slightly less than 90°. The angle of phase defect is the angle by which the phase angle between the capacitor voltage and current is less than 90°. The angles of phase defect for some capacitors having mica dielectrics are as small as three or four minutes. Capacitors having other types of dielectrics may have angles of phase defect greater than one degree. If the angle of phase defect becomes too large, the capacitor has a relatively
high power loss. Such a loss causes an increase in the internal temperature of the capacitor. This temperature rise can shorten the useful life of the dielectric.
Power Factor of a Capacitor
The power factor of a capacitor relates the power losses of a capacitor to its volt-ampere rating. The power factor is the ratio of the power loss to the volt-ampere rating when the capacitor is operated at the rated voltage and frequency. The power factor is usually 0.01 [one percent (1%)] or less for power factor correction capacitors.
Q of a Capacitor
The term Q is used to describe capacitor losses. Q is given by the following expression:
As Q is a relatively large number, it is often simpler to use than the very small power factor values of capacitors.
VOLTAGE RATING OF A CAPACITOR
Capacitors that are used in either ac or dc circuits have a rating known as the dc work- ing voltage. As an example, consider a paper capacitor made with Pyranol and enclosed in a metal container. Such a capacitor may have a rating specified as “600-V dc working voltage.” It is of interest to determine whether this capacitor can be used on a 600-V ac circuit. A previous unit showed that ac voltages are given as effective values that are always 0.707 of the maximum value. The voltage of a 600-V ac circuit reaches a maximum instantaneous value twice in each cycle. This maximum value is
The dielectric of the capacitor is designed for 600 V. Because the ac voltage exceeds this value twice in each cycle, the dielectric can break down and the capacitor can be ruined. This maximum voltage has a short duration. However, the dc working voltage of a capacitor should be high enough to withstand the maximum or peak voltage of an ac circuit.
If the capacitor is not designed for ac service, it may have a short life when operated on ac, even if the applied maximum ac voltage does not exceed the dc working voltage. A capacitor operating on ac has an increase in the power losses. These greater losses may cause excessive internal operating temperatures. This and other factors result in the premature failure of dc capacitors operated on ac. It is recommended that a capacitor be used only in the type of service for which it is designed.
The circuit shown in Figure 6–1 has a maximum value of 141.4 V. The current leads the line voltage by 90°. Because the effective current is one ampere, the maxi- mum value of the current is 1.414 A. The power, in watts, at any instant is equal to the product of the voltage and current values at the same instant. Table 6–1 summarizes
the instantaneous voltage, current, and power values at 15° intervals for the circuit in Figure 6–1.
Wave Patterns for Pure Capacitance
The values in Table 6–1 are plotted against electrical time degrees to obtain the voltage, current, and power waveforms shown in Figure 6–3. Between 0° and 90°, the voltage and the current are positive. The product of the instantaneous voltage and cur- rent values in this part of the cycle will give positive power. This means that the capacitor receives energy from the supply between 0° and 90°. This energy is stored in the electro- static field of the capacitor.
In the period between 90° and 180°, the current rises to its negative maximum value. The impressed voltage is positive and decreases to zero. The product of the instantaneous negative current values and the positive voltage values from 90° to 180° gives negative power. Thus, the capacitor discharges in this period and returns its stored energy to the source.
From 180° to 270°, both the current and the impressed voltage are negative and act together. The product of these instantaneous values (with like signs) gives positive power for this part of the cycle. This means that the capacitor is charging again and storing electrical energy.
The voltage is negative from 270° to 360°. At the same time, the current rises in a positive direction. The product of a negative voltage value and a positive current value gives a negative power value. During this part of the cycle, the capacitor discharges, releasing electrical energy back into the circuit.
Power Waveform. Figure 6–3 shows that for the power waveform, the areas of the two positive pulses of power are equal to the areas of the two negative pulses of power. The positive power pulses represent power fed from the source to the load. The negative pulses of power represent the power returned to the source from the capacitor as it discharges. If the areas of positive power equal the areas of negative power, the net power taken by the capacitor at the end of one complete cycle, or at the end of any number of complete cycles, is zero.
Labels: Alternating current fundamentals
