
CAPACITORS IN PARALLEL AND IN SERIES
Unit 5 explained the methods used to compute the total capacitance for capacitors connected in parallel and in series. Figure 6–4 shows three capacitors connected in parallel. The total capacitance is 55 f.LF. The total capacitive reactance, in ohms, of the three capacitors is less than the reactance of any single capacitor. This is due to the fact that the group has more plate area than a single capacitor.
The capacitive reactance of the three capacitors in parallel is
If a pure inductance is connected to an ac source, the current lags the applied voltage by 90 electrical degrees. This means that no power is lost. The product of the applied voltage and current values is called magnetizing VARs (or VARs). This value does not represent a true power loss. If the pure inductance is a coil having a reactance of one ohm, and an ac voltage of one volt is applied, there will be a current of one ampere lagging by 90°. Under these conditions, the coil requires one magnetizing VAR.
The value of magnetizing VARs for a pure inductance can be calculated using any of the following formulas:
This unit explained that alternating current in a pure capacitance leads the applied voltage by 90°. Thus, no true power is lost in the circuit. It was stated that the product of the applied ac voltage and the current is called VARs. Coil current lags its applied voltage by 90°, and capacitor current leads its applied voltage by 90°. Thus, it can be seen that the capacitor and coil currents act in opposite ways. Coils can be viewed as requiring or consuming magnetizing VARs. Capacitors may be considered as sources of magnetizing VARs.
The magnetizing VARs produced by a pure capacitance can be calculated by any of the following equations:
The minus sign means that the VARs for a capacitor are opposite in direction to those for an inductance.
The principle of the conservation of energy can be applied to steady-state ac circuit theory. This principle states that the total power supplied to a circuit is equal to the sum of the values of power consumed in each of the individual circuit components.
Another principle states that the value of the magnetizing VARs supplied to a circuit is equal to the sum of the magnetizing VAR values required by each of the inductive elements. This quantity is in addition to the sum of all of the magnetizing VARs produced by all of the capacitive elements. Note that the sign of the capacitive VARs is taken as negative.
It will be shown later that the inductive elements of certain circuits require a value of magnetizing VARs equal to that produced by capacitive elements. Such circuits require no external VARs. Thus, when the circuit is viewed from the input terminals, it appears as a pure resistance. This type of circuit is said to be in resonance because there is a balance between the magnetizing VAR supply and the demand.
It is important to understand the similar concepts of conservation of energy and con- servation of magnetizing VARs. In ac power systems, an adequate supply of both watts and magnetizing VARs must be available. Otherwise, the system will not perform as expected. Inductive load equipment such as fluorescent light ballasts, power distribution lines, and induction motors all require capacitors to ensure the supply of magnetizing VARs.
PROBLEM 1
Statement of the Problem
The series circuit in Figure 6–6 consists of a noninductive lighting load with a resistance of 30 !1 and a capacitor with a capacitive reactance of 40 !1. These components are connected across a 200-V, 60-Hz source. The current in the circuit is limited by resistance and by capacitive reactance. Determine the following quantities for this circuit:
1. The impedance, in ohms
2. The current, in amperes
3. The true power, in watts
4. The reactive power, in VARs
5. The apparent power, in volt-amperes
6. The power factor
Solution
1. The impedance in an ac series circuit is the result of combining the resistance in ohms and the reactance in ohms. The reactance may be inductive reactance or capacitive reactance. In the series circuit in Figure 6–6, the resistance and the capacitive
reactance are combined to obtain the impedance. The impedance triangle for this circuit is shown in Figure 6–7. The triangle consists of a base leg of resistance (30!1), an altitude leg of capacitive reactance (40 !1), and a hypotenuse of impedance (50 !1). Note that the impedance triangle for the circuit of Figure 6–6 is inverted. The reason for the position of the impedance triangle will be explained later in this problem. The hypotenuse of the impedance triangle is equal to the square root of the sum of the squares of the other two sides:
2. The line voltage is 200 V. This voltage causes a current in the series circuit of
3. The true power in the circuit is used in the resistance of the circuit because the resistance of the capacitor is negligible. The true power can be found from the formula W I2 R. The value of the lighting load is obtained by multiplying the voltage drop across the lighting load by the current. Another method of determining this load is to divide the resistance into the square of the voltage across the resistor. The actual true power can be computed by any one of the formulas given:
4. The reactive power is known as the magnetizing VARs. This quantity is the product of the current and the voltage at the capacitor terminals. This voltage is 90° out of phase with the current.
5. The apparent power input in volt-amperes for this circuit can be found by either of two methods:
a. Line voltage X line current volt-amperes (VA)
VI 200 X 4 800 VA
b. The input power in volt-amperes is also the result of combining the true power and the magnetizing VARs. This input power is represented in Figure 6–8 as the hypotenuse of a right triangle. The base leg in this case is the true power in watts and the altitude leg is the magnetizing VARs. The power triangle for the circuit is inverted in the same manner as the impedance triangle in Figure 6–7. The input power is the square root of the sum of the squares of the other two sides of the triangle:
6. The input power factor for an ac series circuit is the ratio of the true power, in watts, to the input power, in volt-amperes. In other words, the input power factor is the ratio of the power leg of the power triangle to the hypotenuse. Thus, the power factor is the cosine of the included angle ().
DIAGRAMS FOR THE SERIES CIRCUIT
Figure 6–9 shows the impedance triangle, the power triangle, and the vector diagram for this series circuit. In Figure 6–9C, the voltage across the capacitor is drawn downward from point 0 at a 90° angle with the current vector. This position of the capacitor voltage (V ) indicates that the current leads the voltage by 90 electrical degrees.
Because the impedance triangle is drawn in an inverted position, Figure 6–9A is identical to the triangle of voltages that forms a part of the vector diagram. The capacitive reactance, in ohms, is drawn in a downward direction so that it can be compared to the voltage drop across the capacitor. This drop is shown in a similar direction in the vector diagram. The angle () is in the same position in both the impedance triangle and in the triangle of voltages in the vector diagram.
The power triangle is also drawn in an inverted position. It is similar to the other diagrams. Because the capacitor produces magnetizing VARs, the VARs are shown in a downward direction. Thus, the phase angle () is in the same position for all three diagrams. This means that the line current leads the line voltage.
The student should recognize that the formulas and triangles describing an RL circuit are the same as those describing an RC circuit. However, the VC vector is 180° out of phase
with the V vector.
The power factor of a circuit containing resistance and capacitive reactance can be obtained using the values from any one of the three triangles given in Figure 6–9.
Using values from the impedance triangle, we obtain
The power factor angle (()) for this circuit is 53.1° leading. This means that the line current leads the line voltage by 53.1°.
PROBLEM 2
Statement of the Problem
In the circuit shown in Figure 6–10, a resistor and a capacitor are connected in series. The circuit is connected to a 240-V, 60-Hz line. An ammeter measures a total current of 18.75 A, and a wattmeter indicates a true power of 3375 W. Use the formulas
shown in the Resistive Capacitive (Series) section of Appendix 15 to find the following values:
1. Volt-amperes, apparent power (VA)
2. Volt-amperes-reactive, reactive power (VARs)
3.Capacitive reactance (XC )
4. Capacitance (C)
5.Voltage drop across the capacitor (VC )
6.Resistance of the resistor (VR )
7. Total circuit impedance (Z)
8. Power factor (PF)
9. Angle theta, which indicates the angle at which the voltage and current are out of phase with each other (*0)
Solution
1. Because the applied voltage and total current are known, the apparent power can be computed using the following formula:
2. Now that both the apparent power and the true power are known, the reactive power (VARs) can be computed using the following formula:
3. In a series circuit, the current flow must be the same at any point in a circuit. Because the current flow and reactive power are both known, the capacitive reactance can now be computed using the following formula:
4. The capacitance of the capacitor can be computed using the following formula:
• Charging a capacitor
1. An opposition voltage builds up across the capacitor plates.
2. The charging current has a maximum value when the capacitor is uncharged.
3. The current decreases to zero as the capacitor voltage builds up to equal the source voltage.
4. The current remains at zero amperes while the source voltage equals the opposi- tion voltage of the capacitor.
• Reactance
1. The opposition voltage that develops as a capacitor charges is really a counter- voltage because it opposes the line voltage and limits the current.
2. The current-limiting effect of this countervoltage (capacitance) in an ac circuit is expressed in a unit called capacitive reactance and is measured in ohms
3.The value of X in ohms is inversely proportional to the capacitance in farads and the frequency of the impressed ac voltage.
• Ohm’s law for determining the current, in amperes, in an ac circuit containing capacitance is
• Lead/lag currents
1. Current in a pure resistor is in phase with the voltage.
2. Current in a pure inductive reactance lags the impressed voltage by 90 electrical degrees.
3. Current in a circuit with pure capacitive reactance leads the impressed voltage by 90 electrical degrees.
• Angle of phase defect
1. The phase angle between the capacitor voltage and current is slightly less than 90°.
2. In some capacitors having mica dielectrics, the angle of phase defect is as small as three or four minutes.
3. Capacitors having other types of dielectrics may have angles of phase defect greater than one degree, causing high power loss.
4. If the angle of phase defect is too large, the internal temperature of the capacitor may increase and shorten the useful life of the dielectric.
• The power factor of a capacitor relates the power losses of a capacitor to its volt-ampere rating.
1. The power factor is the ratio of the power loss to the volt-ampere rating when the capacitor is operated at the rated voltage and frequency.
2. The power factor is usually 0.01 (1%) or less for power factor correction capacitors.
• The term Q describes capacitor losses and is expressed as
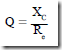
• Q is a relatively large number and is easier to use than the small values of the power factors for capacitors.
• The dc working voltage of a capacitor should be high enough to withstand the maxi- mum or peak voltage of an ac circuit:
• A capacitor should be used only for the type of service for which it is designed.
• The power in a capacitor, in watts, at any instant is equal to the product of the voltage and current values at the same instant.
• The true power or net power taken by the capacitor at the end of one complete cycle, or at the end of any number of complete cycles, is zero.
• Magnetizing VARs are present in a pure inductive circuit where the current lags the applied voltage by a value up to 90 electrical degrees.
• Magnetizing VARs are present in a pure capacitive circuit where the current leads the applied voltage by a value up to 90 electrical degrees.
• Magnetizing VARs are represented by the product of the applied voltage and the current. (This value does not represent a true power loss.)
• For a pure inductance:
(The minus sign means that the VARs for a capacitor are opposite to those for an inductance.)
• Coils consume magnetizing VARs, and capacitors supply magnetizing VARs.
• A circuit is in resonance when
1. the circuit is viewed from the input terminals and it appears to be pure resistance.
2. there is a balance between the magnetizing VAR supply and the demand.
3. the inductive elements of certain circuits receive a value of magnetizing VARs equal to that produced by the capacitive elements.
• The conservation of energy principle states that the total power supplied to a circuit is equal to the sum of the values of power consumed in each of the individual circuit components.
• In an ac power system, an adequate supply of watts and magnetizing VARs must be available if the system is to perform as expected.
• Inductive load equipment, such as fluorescent light ballasts, power distribution lines, and induction motors, all require capacitors to ensure an adequate supply of magnetiz- ing VARs.
Achievement Review
1. What is capacitive reactance?
2. Three capacitors are connected in parallel across a 230-V, 60-Hz supply. These capacitors have values of 10 f.LF, 30 f.LF, and 60 f.LF.
a. A single capacitor can replace the three capacitors. What value of capacitance is required to do this?
b. Determine the total current taken by the three capacitors.
c. What is the current in the 10-f.LF capacitor?
3. The three capacitors in question 2 are reconnected in series across the same ac supply.
b. Assuming that this same capacitor is connected across a 240-V, 25-Hz source, determine
(1) the capacitive reactance, in ohms.
(2) the current, in amperes.
c. Give reasons for any differences in the capacitive reactance and the current in parts (a) and (b) of this problem.
5. Explain what is meant by the term angle of phase defect.
6. A capacitor has an angle of phase defect of 1.2°.
a. What is the actual angle by which the current leads the impressed voltage for this capacitor?
b. What is its power factor?
7. A noninductive load with a resistance of 30 !1 is connected in series with a capacitor. The capacitor has a capacitive reactance of 25 !1 and negligible resis- tance. The series circuit is energized from a 210-V, 60-Hz source. Determine
a. the impedance of the series circuit.
b. the current, in amperes.
c. the loss in volts across the noninductive resistance load.
d. the loss in volts across the capacitor.
8. For question 7, determine
a. the power in watts expended in the series circuit.
b. the volt-amperes-reactive component for the series circuit, in VARs.
c. the apparent power, in volt-amperes.
d. the circuit power factor.
e. the power factor angle for this circuit.
9. For the series circuit in question 7, draw the following diagrams using con- venient scales:
a. An impedance triangle
b. A power triangle
c. A vector diagram
10. What is the rating, in microfarads, of the capacitor used in the series circuit in question 7?
11. An experimental series circuit consists of a noninductive variable resistor con- nected in series with a 1-f.LF capacitor of negligible resistance. The variable resis- tor has a maximum resistance of 5000 !1. This series circuit is connected across a 50-V, 60-Hz source.
a. If the current is to lead the line voltage by a phase angle of 45°, what is the resistance in ohms that must be inserted in the series circuit by adjusting the variable resistor?
b. What is the current in this series circuit?
c. What is the power factor of this circuit?
d. What is the power expended in the circuit?
12. In question 11, determine
a. the loss in volts across the variable resistor.
b. the loss in volts across the capacitor.
c. the volt-ampere reactive component (VARs) for the capacitor.
d. the apparent power for the entire series circuit.
13. For the circuit in question 11, draw the impedance triangle and the vector dia- gram, using convenient scales.
14. A paper capacitor can be used in ac and dc circuits. It has a dc working voltage of 500 V. Can this capacitor be connected directly across a 440-V, 60-Hz source?
15. A capacitor is connected across a 120-V, 60-Hz supply. An ammeter indicates 5 A and a wattmeter indicates 10 W. Determine
a. the resistance of the capacitor.
b. the power factor.
c. the phase angle to the nearest tenth of a degree.
d. the angle of phase defect to the nearest tenth of a degree.
Labels: Alternating current fundamentals