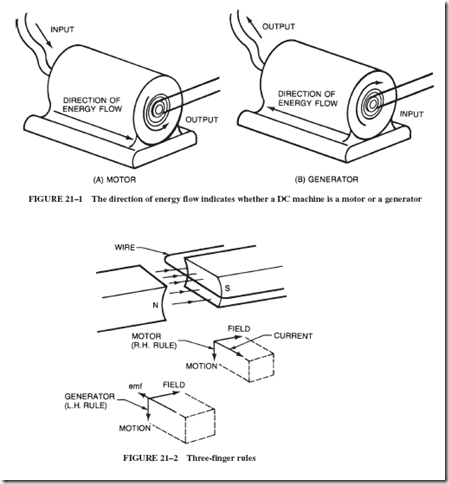
The brief introduction to motors provided by Chapter 20 points to great similarities between motors and generators. Certainly their physical design features are so similar that often it is impossible, without close inspection, to tell a motor from a generator. In fact, there are a few machines that can be used either as a motor or as a generator.
All electrical machines are essentially energy converters. It is the direction of the energy flow through the machine that determines its name and function. Figure 21–1 illustrates this idea.
Both machines are look-alikes with their armature, field poles, commutators, and such. Where they differ is in the opposite application of electromagnetism. This fact is
emphasized by the contrast between Fleming’s left-hand rule for generators versus the right-hand rule for motors. If you compare Figure 20–6 with Figure 18–4, you may notice that for any two quantities that are the same, the third one is exactly the opposite. The same idea is conveyed by Figure 21–2. This fact has some significant consequences, as we shall see in the following section.
21–2 THE COUNTER-emf IN A MOTOR
When a coil of wire is rotated within a magnetic field, it generates an emf, regardless of what causes its motion. It does not necessarily take an external agent sup- plying muscle energy to the crank on a shaft, as implied by Figure 21–1B. It can be electromagnetic motor action that sets the armature spinning and starts to generate an emf. In other words, every motor inadvertently acts like a generator and produces a volt- age within itself while it is running. This voltage is known as counter-emf (cemf ), because its polarity is such that it opposes the applied line voltage; see Figure 21–3.
Like the output voltage from a generator, the amount of cemf depends on two factors:
1. The strength of the magnetic field
2. The speed of rotation
We can, in fact, use the generator formula, first introduced in Section 19–8, to calculate the cemf generated within the motor.
EXAMPLE 21–1
It may surprise some students to see that the cemf is nearly as high as the applied voltage. In fact, it is sometimes difficult for a beginner to realize the value of the emf that a motor generates. The generated emf is a measure of the useful mechanical energy obtained from the electrons passing through the armature.
As stated before, this emf is called counter-emf or back-emf because it opposes the voltage applied to the motor. This is a useful sort of opposition. The generated back-emf opposes the movement of the incoming electrons in the same way that the weight of a sack of groceries opposes the efforts of a boy carrying the sack up a flight of stairs. If there is no opposition, no useful work is done. If the boy leaves the groceries on the sidewalk, he can run upstairs faster, but the groceries are not delivered. An electric heater element generates no back-emf; the electrons can run through it rapidly, but they produce no mechanical work.
It is easy to make an adjustment on the electric motor so that it generates no counter-emf. Merely bolt down the armature so that it cannot turn. Then electrons run through the motor faster and more easily, and the motor is converted into an electric heater.
The example we used before had a line voltage of 120 volts applied. This power line has two jobs to do: First, it must supply 100 volts, which is converted to mechanical energy. Second, it must supply enough additional voltage to force the 10-ampere current through the 2-ohm wire resistance. It takes 20 volts to put 10 amperes through 2 ohms; thus, the line voltage must be 100 + 20 = 120 volts.
Carry this calculation one step further. Multiply the total applied voltage (120 volts) by the current (10 amperes) and find the total power input, 1,200 watts.
Generated voltage (100 volts) times 10 amperes equals the useful mechanical power output, 1,000 watts. This same figure was found once before: the 1.34 horsepower output that was found from torque and rpm (Chapter 20).
The power input is 1,200 watts; the output is 1,000 watts. Where did the other 200 watts go? By multiplying the 20 volts used on resistance by the 10 amperes, we get 200 watts. This represents the rate at which energy is converted into heat in the armature. The rate of heat production is 200 watts.
The counter-emf does not produce useful mechanical energy, but the useful power produced can be calculated from the counter-emf and the current. This is just like saying that the useful power (working rate) accomplished by the grocery bagger can be calculated from the weight of the sack and the speed with which he lifts it. The weight is not doing the work; but the greater the weight, the more work done by the bagger.
EXAMPLE 21–2
Given: A 5-ohm armature taking 6 amperes from a 115-volt line when operating at its normal rating.
a. Counter-emf generated
b. Power input
c. Useful power output
d. Heating rate
e. Efficiency
f. Current and heating rate if the motor is stalled
Solution
21–3 ARMATURE WINDINGS
As pointed out in Section 19–2, two main types of drum armature windings are in use: the lap winding and the wave winding. In Figure 21–4 (as in Figure 19–14), the innermost circle of numbered rectangles represents an end view of commutator bars. The next circle of 12 distorted rectangles represents sections of the face of the armature. (A different view of the face sections is shown in Figure 21–5.)
Outside of the rectangles in Figure 21–4, representing the cylindrical armature face, are lines showing the coil connections at the back of the armature. (This information is not visible in a diagram such as Figure 21–5.) The field poles represent a four-pole field in which this armature is to rotate. (Note the simplified view of the field structure in Figure 21–5.)
The Lap Winding
A few minutes spent in tracing the wiring in Figure 21–4 makes the pattern seem less complicated, since the 12 coils on this armature are all alike. Start with the negative
brush touching bar 1. Electrons flowing from the DC supply line to bar 1 can escape into the winding by either of two paths. (The brushes are shown as if inside, rather than in their actual position outside.)
Follow the heavily shaded wire through slot 1 and back through slot 4. The main feature of the lap winding is that the finish end of this coil, coming through slot 4, is connected to commutator bar 2, next to the one from which we started (1). From bar 2 the current path is through slot 2, back by slot 5 to bar 3. Then the current path goes out slot 3 and back by slot 6 to bar 4. Bar 4 is in contact with a positive brush that completes the circuit to the DC power source. Returning again to bar 1, another path can be traced through slots 3, 12, 2, 11, 1, and 10, back to the other positive brush.
Note that under both N poles, the current is away from the commutator. Under both S poles, the current is toward the commutator. With the help of Figure 21–5 and the three-finger right-hand rule, determine the direction of rotation of the armature.
Figure 21–6 is a schematic view of the circuits through this four-pole armature. Each numbered rectangle corresponds to a numbered commutator bar, as shown in Figure 21–4. The purpose of this sketch is to show that there are four parallel paths through this armature.
There are so many variations in armature windings that the subject can merely be in- troduced in these few pages; for the whole story, consult a text dealing only with armatures.
In general, lap windings require
• As many brushes as there are poles
• As many parallel paths through the armature as there are poles
The Wave Winding
Figure 21–7 shows another pattern called the wave winding. Compare it with the lap winding. Notice that the wave winding accomplishes a similar control of current direction in the wires under each field pole, so that rotation is produced. (One need not be concerned because the wires in slot 7 carry currents in opposite directions, which oppose and therefore cancel each other. Because slot 7 is between field poles at the instant shown, there is no force on the wires anyway.)
To see the difference between wave winding, Figure 21–7, and lap winding, Figure 21–6, observe the heavily shaded wire that starts from bar 1. The ends of the coil are spread apart, connecting to widely separated bars in wave winding rather than to adjacent bars as in lap winding.
Eleven bars and slots, rather than 12, are used in wave winding, because a 4-pole wave winding does not fit on a 12-bar, 12-slot armature. The reason for this difference, as well as the reasons for the locations of the commutator connections, involves calculations not worked out here.
Trace through or (better yet) redraw the winding, starting with a sketch that does not show the wiring. Begin at bar 1, through slot 1, over to slot 4, to bar 6, out slot 6, to slot 9, to bar 11, continuing around the armature until bar 4 is finally reached. There is another path from bar 1, out slot 10, in slot 7, and so forth, again finally arriving at bar 4.
Figure 21–8 shows, in schematic fashion, that there are only two parallel paths through this armature. (The numbered rectangles correspond to the commutator bars in Figure 21–7.)
Wave windings require
• A minimum of two brushes but a maximum of as many brushes as poles
• Only two parallel paths through the armature in one complete wave winding, regard- less of the number of brushes
Comparative Uses
Lap windings are good for high-current, low-voltage motors because they have more parallel paths for the current. Wave windings are good for high-voltage, low-current motors and generators because they have more coils in series.
Up to this point, we have assumed that the armature rotates in the field of a permanent magnet. Actually, until recent times, motors with permanent magnetic fields have had limited applications in industry. Although this trend is changing (see Section 21–11), most industrial motors have traditionally used, and still use, electromagnets for their field structure.
Field-magnet coils may be in series, or in parallel, or one in series and one in parallel with the armature, as in compound-wound motors, which have two sets of windings. The behavior of these magnetic field windings and their effect on motor performance is the subject of the next chapter.
Labels: Direct current fundamentals